布尔逻辑的应用
引言
您是否曾想过计算机是如何完成像支票簿核算、下棋或文档拼写检查那样的工作的?仅仅在几十年之前,这些事情只有人类才可以完成,而现在计算机便可以轻轻松松地完成这些任务。令人好奇的是,由硅和导线制成的“芯片”究竟是如何完成看起来需要人类思维才能完成的工作的?
如果您希望从本质上深入了解这一问题的答案,首先需要了解布尔逻辑的概念。布尔逻辑最初是由乔治·布尔于19世纪中叶提出的,它可将许多意想不到的事情映射为位和字节。有关布尔逻辑最重要一点是,一旦您真正掌握了它,就会觉得布尔逻辑(或者理解计算机工作方式所需的最基本的知识)相当简单。在本篇博闻网文章中,我们将首先讨论一些简单的逻辑“门电路”,然后了解如何将这些门电路进行组合以实现一些有用的元件。
简单的门电路
您需要了解三种、五种或七种简单的门电路,具体取决于您要采用的门电路种类计算方式(很快您就会知道原因)。您可以对这些简单的门电路进行组合,以实现任何想要的数字元件。这些门电路看起来有些枯燥,并且极其简单,但在下面几节中我们将看到一些有趣的组合,这些将使你感到兴奋。如果您还不了解位和字节的概念,请在继续之前阅读位和字节,这将会很有帮助!
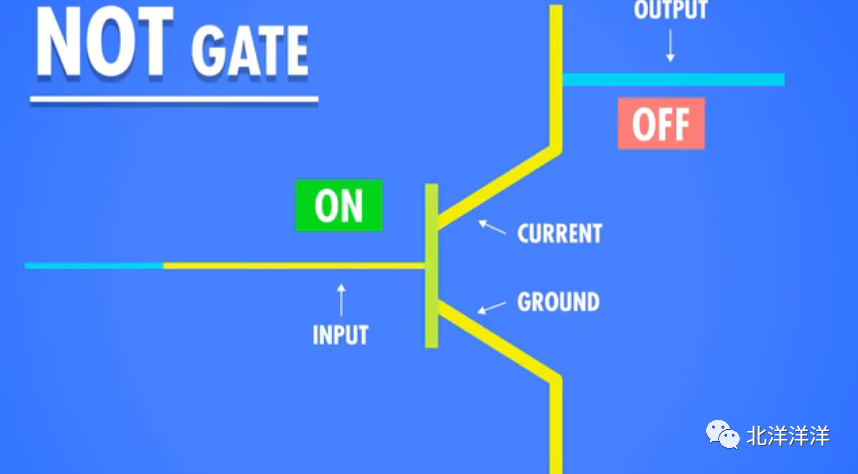
最简单的门电路称为“反相器”,也叫做非门。这种门电路的输入为0或1,而输出则为其反相即1或0。下表显示了非门的逻辑表以及在电路图中用来表示非门的标准符号:
|
| |||||||
|
|||||||
可以在该图中看到非门有一个称为A的输入端和一个称为Q(用“Q”表示输出是因为如果使用了“O”,会很容易与0混淆)的输出端。该表显示了非门的工作方式,并且原理非常简单:将0应用于A时,Q会产生1;将1应用于A,则Q会产生0。
与门对两个输入A和B执行逻辑“与”运算:
|
| ||||||||||||||||
|
||||||||||||||||
与门的工作原理是”如果A和B都为1,则Q应该为1。“您可以在与门的逻辑表中查看其工作方式。逐行阅读该表,如下所示:
|
| ||||||||||||||||||||
| ||||||||||||||||||||
下一种门电路是或门。其基本工作原理是“如果A为1,或B为1(或两者都为1),则Q为1。”
|
| ||||||||||||||||
|
||||||||||||||||
以上为三种基本的门电路(此为门电路种类的一种计算方法)。通常还需知道其他两种门电路:与非门和或非门。这两种门电路不过是与门或者或门与非门的组合。如果将这两种门电路包括在内,则门电路将增加到5 种。以下是与非门和或非门的基本工作方式——您会发现它们不过是与门和或门的相反状态:
|
| ||||||||||||||||
|
||||||||||||||||
|
| ||||||||||||||||
|
||||||||||||||||
有时还会将另外两种门电路——异或门和异或非门——包括在门电路种类中,以下是这两种门电路的逻辑表:
|
| ||||||||||||||||
|
||||||||||||||||
|
| ||||||||||||||||
|
||||||||||||||||
异或门的工作原理是:如果A或B为1,但不是两者都为1,则Q为1。门电路种类中不包括异或门的原因是您可以使用先前列出的三种原始的门电路来实现异或门。下面提供了一种实现方法:
如果尝试A和B的所有四种不同输入模式并跟踪相关电路,您会发现Q的工作方式类似于异或门。由于异或门的符号很容易理解,因此通常将异或门视为“标准门电路”,并且在电路图中像使用与门和或门一样来使用该门电路会更为简单。
简单的加法器
在位和字节一文中,您已经了解了二进制加法。本节中,您将了解如何使用上一节介绍的门电路来创建能够执行二进制加法的电路。
让我们先了解一下一位加法器。假定您现在需要将一位数加在一起并算出答案,为此开始设计电路时所采用的方式是首先查看所有逻辑组合。您可以查看以下四组数的求和:
| 0 | 0 | 1 | 1 |
| + 0 | + 1 | + 0 | + 1 |
| 0 | 1 | 1 | 10 |
在您遇到1+1之前,一切情况都很正常。在1+1的情况下,您需要考虑比较麻烦的进位问题。如果不考虑进位(因为这毕竟是1位加法问题),您会发现可通过异或门电路来解决此问题。但是如果考虑进位,则可能要改写等式,从而始终包括2位输出,如下所示:
| 0 | 0 | 1 | 1 |
| + 0 | + 1 | + 0 | + 1 |
| 00 | 01 | 01 | 10 |
通过这些等式,您可以生成下面的逻辑表:
|
| ||||||||||||||||||||
| ||||||||||||||||||||
通过查看该表,您会发现可通过异或门电路来实现Q,通过与门电路来实现CO(进位输出)。一切都很简单。
如果要将两个8位的字节加在一起,又要如何处理呢?实现该操作要稍微难一些。最简单的方法是将该问题模块化为可重用的元件,然后复制这些元件。这种情况下,我们只需要创建一个元件:全二进制加法器。
我们发现全加法器和上述加法器之间的差别在于全加法器可将A、B输入与进位输入(CI)输入相加。拥有全加法器之后,我们可以将8个这样的全加法器串接在一起,从而形成一个字节宽的加法器,并将进位输入从一个加法器级联到另一个加法器。
与我们前面使用的逻辑表相比,全加法器的逻辑表稍微复杂一些,原因是我们现在有3个输入位。该逻辑表如下所示:
|
| |||||||||||||||||||||||||||||||||||||||||||||
| |||||||||||||||||||||||||||||||||||||||||||||
有多种不同的方法来实现该表,在此我们将介绍一种易于理解的方法。如果您查看Q位,会发现顶部4位的工作方式与针对A 和B的异或门电路类似,而底部4位的工作方式与针对A和B的同或门电路类似。同样,CO顶部4位的工作方式与针对A和B的与门电路类似,而底部4位的工作方式则和或门电路类似。根据这些事实,下面的电路可实现全加法器:
这当然不是实现全加法器最有效的方法,但却极易理解,并且很容易跟踪使用该方法的逻辑。如果有兴趣,您可以思考一下如何使用更少的门电路来实现该逻辑。
现在我们有了一个名为“全加法器”的功能。计算机工程师下一步要做的是将全加法器装在“黑盒子”中,这样他就不用考虑该元件的细节了。用于全加法器的黑盒子将如下所示:
通过这个黑盒子,现在很容易就可画出一个4位全加法器:
在该电路图中,每一位的进位输出将直接输入到下一位的进位输入。通过硬连线方式将最初的进位输入位设为0。如果在A和B线路上输入两个4位的数字,则将会在Q线路上获得该4位数的和输出,另外还有1位用来表示最终进位输出。你会发现该链可随意扩展,如果需要,可扩展到8位、16位或32位。
我们刚刚创建的4位加法器称为行波进位加法器。之所以称为行波进位加法器,是因为进位位像波纹一样从一个加法器输入到另一加法器。该实现方式的优点在于它非常简单,但其缺点是存在速度问题。在实际电路中,门电路的状态切换需要时间(该转换时间属于纳秒级,但对于高速计算机来说纳秒也是很重要的)。由于存在行波进位,因此32或64位的行波进位加法器可能需要100到200纳秒来获得最终的求和结果。为此,工程师创建了更高级的名为先行进位加法器的加法器。实现先行进位加法器所需的门电路数量很大,但是该加法器在计算速度上大有改进。
触发器
通过布尔门电路可以实现的一项更为有趣的功能是形成记忆。如果门电路的连接正确,它们将会记住输入值。这一简单概念成为计算机中RAM(随机存取存储器)的基础,并且还使得创建其他各种有用的电路成为可能。
记忆依赖于一个名为反馈的概念,也就是说门电路的输出将反馈给输入。下面显示的是使用两个反相器的最简单的反馈电路:
如果沿着反馈路线,则会看到如果Q为1,则它始终为1;如果Q为0,则它始终 0。由于有必要控制所创建的电路,因此上面的电路没有多大用处,但它能够使您了解反馈的工作方式。
事实上,在“真正”的电路中,可使用这类简单的反相器反馈方法。下面显示了一种更有用的使用两个与非门电路的反馈电路:
该电路有两个输入(R和S)和两个输出(Q和Q')。由于存在反馈,因此该电路的逻辑表与先前看到的逻辑表相比有些不同。
| R | S | Q | Q' |
| 0 | 0 | 非法 | |
| 0 | 1 | 1 | 0 |
| 1 | 0 | 0 | 1 |
| 1 | 1 | 记忆 |
从逻辑表可以看到:
- 如果R和S的状态相反,则Q与S相同,且Q'与Q相反。
- 如果R和S同时切换为1,则电路会记住R和S上先前显示的内容。
有趣的是,该逻辑表中还有一种非法状态。在这种状态下,R和S都为0,在此状态下没有记忆值。由于存在非法状态,因此通常要在输入端添加一些条件逻辑以防止出现这种状态,如下图所示:
在该电路中,有两个输入(D和E)。您可以将D视为“数据”,并将E视为“启用”。如果E为1,则Q的状态将与D相同。但是如果E更改为0,则Q将会记住在D上最后看到的内容。以这种方式运行的电路通常称为触发器。
触发器的一种常见形式是J-K触发器。人们并不清楚“J-K”名称的历史来由,但通常它会出现在一个黑盒子中,如下所示:
在该示意图中,P代表“预设”,C代表“清除”,Clk代表“时钟”。该逻辑表如下所示:
| P | C | Clk | J | K | Q | Q' | |
| 1 | 1 | 1到0 | 1 | 0 | 1 | 0 | |
| 1 | 1 | 1到0 | 0 | 1 | 0 | 1 | |
| 1 | 1 | 1到0 | 1 | 1 | 切换 | ||
| 1 | 0 | X | X | X | 0 | 1 | |
| 0 | 1 | X | X | X | 1 | 0 |
该表表明:首先,“预设”和“清除”完全覆盖J、K和Clk。因此,如果“预设”变为0,则Q将变为 1;如果“清除”变为0,则Q将会变为0(不管J、K和Clk执行何种操作)。但是,如果“预设”和“清除”都为1,则J、K和Clk均可执行。1到0符号表示时钟从1更改为0时,如果J和K的状态相反,则将记住J和K的值。在时钟的下降沿(从1到0的转换),将存储J和K。但是,如果J和K在下降沿上正巧都为1,则Q只能切换。也就是说,Q将从当前状态变为相反的状态。
现在你可能会问自己:“这究竟会带来什么益处?”事实上,“跳变沿触发”概念是非常有用的。J-K触发器仅“锁存”从1转换为0时的J-K输入,这一事实使其作为一种记忆设备更为有用。J-K触发器对计数器(广泛用于创建数字时钟)同样也很有用。以下是一个使用J-K触发器的4位计数器示例:
该电路的输出是A、B、C和D,并且它们表示一个4位的二进制数字。在最左侧的触发器的时钟输入端,会输入一个反复从1变为0再变回1的信号(振荡信号)。计数器将对该信号中的下降沿计数。也就是说,每次输入信号从1更改为0时,由A、B、C和D表示的4位数将增加1。因此计数将从0变为15,然后再循回到0。您可以向计数器添加任意多的位数,并且可随意计数。例如,如果在门上放置一个磁力开关,则计数器将会计算开门和关门的次数。如果在公路上放置一个光学传感器,则计数器可计算驶过的汽车的数量。
J-K触发器的另一用途是用于创建跳变沿触发的锁存,如下所示:
在这种排列下,时钟跳变沿从低变为高时将“锁存”D上的值。锁存器对于诸如计算机的CPU和外围设备之类的设计来说至关重要。
实现门电路
在前几节中,我们了解到通过使用非常简单的布尔门电路,可以实现加法器、计数器、锁存器等。这一进步具有伟大的意义,因为在不久以前有些事只有人类才能做到,比如对两个数字进行相加。通过完成少量的工作,人们不难设计出可执行减法、乘法、除法等运算的布尔电路。可以看到,要设计出便携式计算器并不是那么遥不可及。因此,设计出可用于计算机的成熟的CPU也并非没有可能。
在现实生活中我们应该如何实现这些门电路?布尔先生以书面形式提出了这些门,采用这种形式使它们看起来很不错。但是,若要使用这些门电路,我们需要真正实现这些门电路以便它们可以主动执行逻辑运算。实现这一飞跃之后,我们就已经开始了创建真正的计算设备的工作。
了解有关布尔逻辑的物理实现最简便的方法是使用继电器。实际上,这是最早的几台计算机的实现方式。如今没有人再通过继电器来制成计算机,人们现在使用蚀刻在硅片上的亚显微晶体管。这些晶体管的体积之小、速度之快都令人难以置信,与继电器相比,它们所消耗的电能非常少。但是,继电器的原理很容易理解,并且也非常易于实现布尔逻辑。由于其简单性,您将能够看到从“书面形式表示的门电路”转变为“在现实世界中实现的有源门电路”是可行的,并且能够直接转换,从而使得使用晶体管执行这一转变也很容易。
让我们先来看看反相器吧。通过继电器实现非门是很简单的:我们要做的就是通过电压来表示位状态。将二进制1定义为6伏并将二进制0定义为0伏(接地)。然后将使用6伏的蓄电池来为电路提供电源。因此非门将如下图所示:
如果您看不懂该图是什么意思,请阅读继电器工作原理以获取详细说明。
可以看到,在该电路中如果A端的输入电压为0伏,则在Q端可获得6伏输出;如果A端的输入电压为6伏,则在Q端可获得0伏输出。通过继电器很容易实现反相器!
通过两个继电器来实现与门也同样简单:
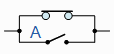
在此您可以看到如果A和B端的输入电压均为6伏,则Q端电压为6伏。在其他情况下,Q端则为0伏,这正是我们想通过与门实现的结果。或门更为简单——仅将A和B两条电线连在一起就可形成或门电路。如果将两个继电器并联,您会得到更加令人意想不到的结果。
从讨论中可以看到,您可以通过继电器创建三种基本的门电路:非门、或门及与门。然后使用上面显示的逻辑电路图将这些物理门电路连接在一起,以创建物理的8位行波进位加法器。如果使用简易开关将A和B输入应用到加法器并将所有8条Q线路与灯泡连接,则能够将任意两个数字相加并读取灯上的结果(“灯亮”=1,“灯灭”=0)。
以简单门电路形式表示的布尔逻辑非常直白易懂。通过简单门电路,您可创建更复杂的函数,例如加法运算。在现实中可以实现门电路且非常容易。通过了解以上三项内容,您已经掌握了数字化革命的核心,并从根本上了解了计算机的工作方式。
 电子发烧友App
电子发烧友App













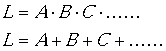










评论