串联谐振电路实验

串联谐振电路实验

一 、实验目的

1、 通过实验掌握串联谐振的条件和特点，测绘RLC串联谐振曲线。

2、研究电路参数对谐振特性的影响。

二、实验原理

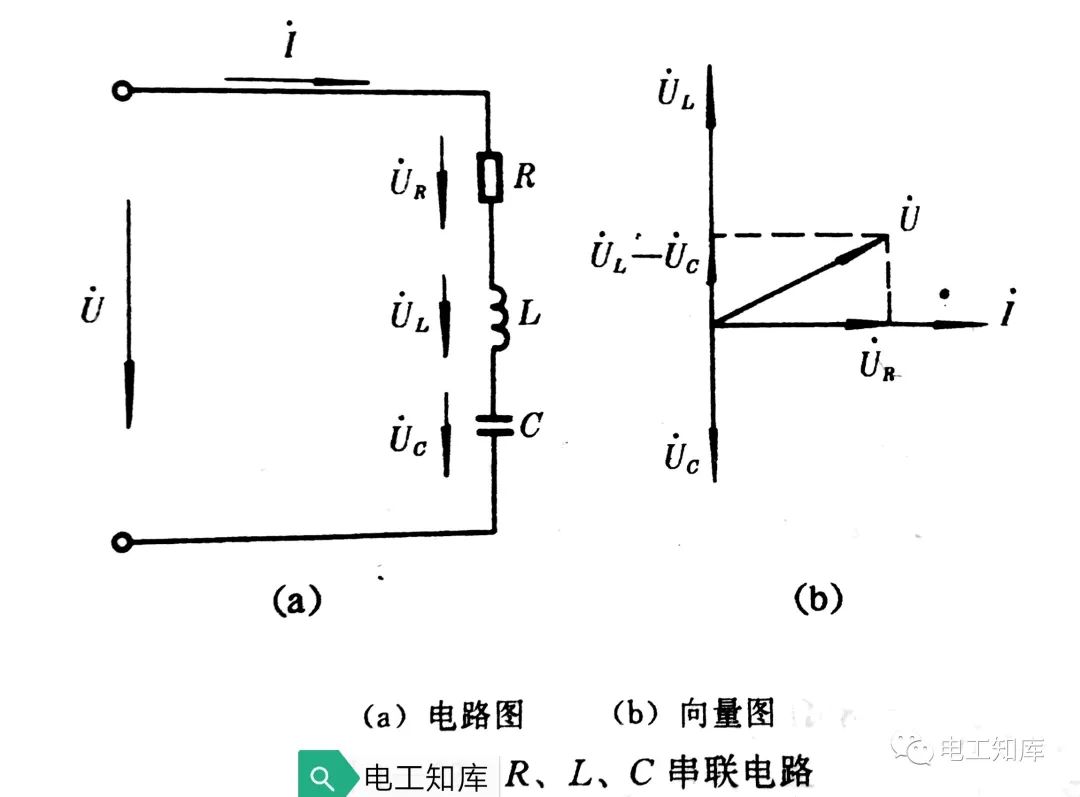
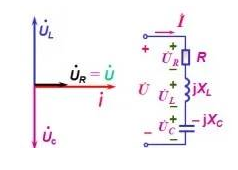
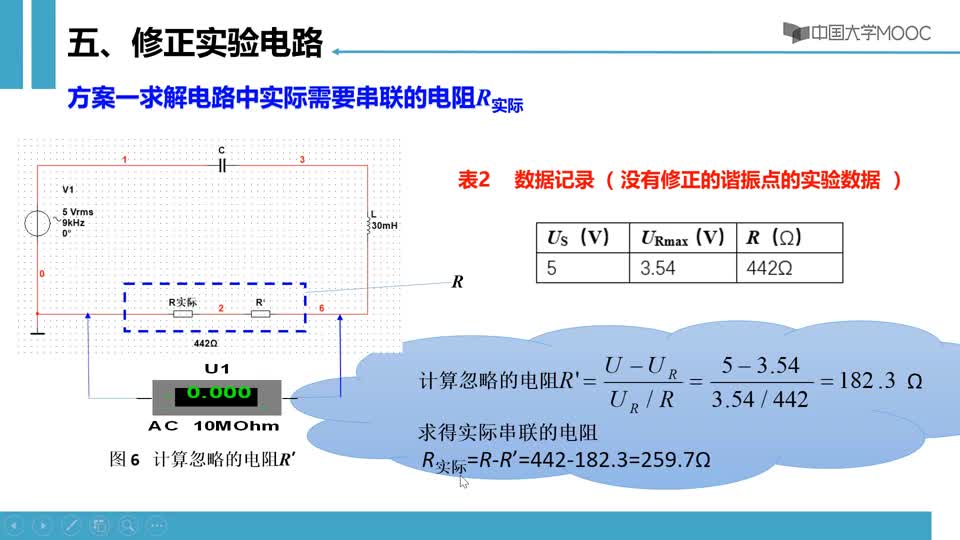
在图7-1所示的RLC串联电路中，若取电阻R两端的电压U2为输出电压，

则该电路输出电压与输入电压之比为：

U2 / U1 =R / [R+j（ωL－1/ωC）]

=R /√R2+(ωL－1/ωC)2∠tg-1(ωL－1/ωC) / R     （7-1）

由上式可知，输出与输入电压之比是角频率ω的函数。当ω很高和ω很低时，比

值都将趋于零，而在某一频率ω=ω0时，可使ω0L－1/ω0C =0，输出电压与输入

电压之比等于1，电阻R上的电压等于输入电源电压达到最大值，电路阻抗最小，

电抗为零，电流达到最大且与输入电压同相位。电路的这种工作状态叫做RLC

串联谐振。谐振的条件：

ω0L－1/ω0C = 0

或                ω0 = 1/√LC                              （7-2）

改变角频率ω时，振幅比随之变化，振幅比下降到峰值的1/√2 = 0.707对应的两

个频率ω1,ω2（或f1和f2）之差称为该网络的通频带宽。

BW=ω2－ω1      
 
理论上可以推出通频带宽

BW=ω2－ω1=R/L      （7-3）
   
由（7-3）式可知网络的通频带取决于

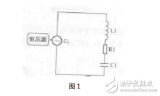
电路的参数。RLC串联电路幅频特性曲线的陡度，可以用品质因素Q来衡量，

Q的定义为：

Q =ω0 /BW=ω0L/R=1/ω0C

可见品质因数Q也取决于电路参数。当L和C一定时。电阻R越小，Q值越大，

通频带越窄，谐振曲线越陡峭。反之，电阻

R越大，品质因数Q越小，通频带宽亦越

宽，曲线越平缓，如图7-2所示。

设R1＞R2，当电路发生串联谐振时，

XL=XC、Z=R2

则    BW1=ω2－ω1＞BW2=ω‘2－ω‘1

I=U1/Z=U1/R

UR=IR

UL=jIXL=jIω0L=jU/Rω0L=jQU1

Uc=-jIXc=I/jω0C=-jQU1

当 XL=XC＞R时，UL=UC＞＞U

电路的这一特点，在电子技术通讯电路中得到广泛的应用，而在电力系统中则应

避免由此而引起的过压现象。
 
2、 实验内容及步骤

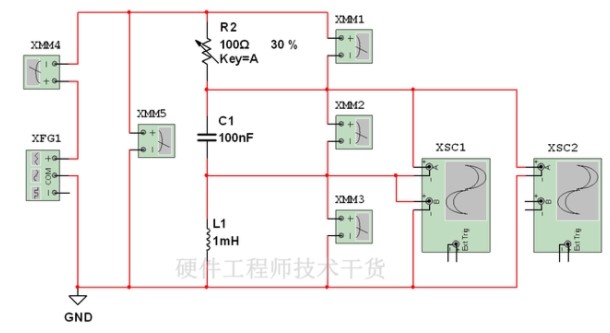
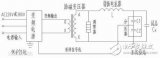
a) 将动态电路板TS-B-27、正弦信号发生器、电阻R、电感L、电容C按

b) 图7-3联成电路。r 为电感线圈电阻,L=33mH，C= 0.10μF，R=620Ω。

c) 调节正弦信号源输出电压，使U1=3V，调节正弦信号输出频率,使之为表

7-1中的数值,测量U2，UC，UL，填入表7-1中 。