第5节 基尔霍夫定律

基尔霍夫定律是电路中电压和电流所遵循的基本规律，是分析计算电路的基础。它包括两方面的内容，其一是基尔霍夫电流定律，简写为KCL定律，其二是基尔霍夫电压定律，简写为KVL定律。它们与构成电路的元件性质无关，仅与电路的连接方式有关。

为了叙述问题方便，在具体讨论基尔霍夫定律之前，首先以图1．32为例，介绍电路模型图中的一些常用术语。

• 支路

将两个或两个以上的二端元件依次连接称为串联。单个电路元件或若干个电路元件的串联，构成电路的一个分支，一个分支上流经的是同一个电流。电路中的每个分支都称作支路。如图1．32中ab、ad、aec、bc、bd、cd都是支路，其中aec是由三个电路元件串联构成的支路，ad是由两个电路元件串联构成的支路，其余4个都是由单个电路元件构成的支路。

• 节点

电路中3条或3条以上支路的连接点称为节点。如图1．32中a、b、c、d都是节点。

• 回路

电路中的任一闭合路径称为回路。如图1．32中abda、bcdb、abcda、aecda、aecba等都是回路。

• 网孔

平面电路中，如果回路内部不包含其它任何支路，这样的回路称为网孔。因此，网孔一定是回路，但回路不一定是网孔。如图1．32中的回路aecba、abda、bcdb都是网孔，其余的回路则不是网孔。

连接在同一个节点上的各支路的电流，必然受到KCL定律的约束；任意一个闭合回路中各元件上的电压，必然受到KVL定律的约束。这种约束称为互连约束，亦即元件连接方式的约束。互连约束关系是线性关系。

1.5.1  基尔霍夫电流定律

KCL定律是描述电路中任一节点所联接的各支路电流之间的相互约束关系。KCL定律指出：对电路中的任一节点，在任一瞬间，流出或流入该节点电流的代数和为零。即：

在直流的情况下，则有：

通常把式（1．19）、（1．20）称为节点电流方程，简称为KCL方程。

应当指出：在列写节点电流方程时，各电流变量前的正、负号取决于各电流的参考方向对该节点的关系（是“流入”还是“流出”）；而各电流值的正、负则反映了该电流的实际方向与参考方向的关系（是相同还是相反）。通常规定，对参考方向背离节点的电流取正号，而对参考方向指向节点的电流取负号。

例如，图1．33所示为某电路中的节点a，连接在节点a的支路共有五条，在所选定的参考方向下有：

-I₁+I₂+I₃-I₄+I₅=0

KCL定律不仅适用于电路中的节点，还可以推广应用于电路中的任一假设的封闭面。即在任一瞬间，通过电路中的任一假设的封闭面的电流的代数和为零。

例如，图1．34所示为某电路中的一部分，选择封闭面如图中虚线所示，在所选定的参考方向下有：

I₁-I₂-I₃-I₅+I₆+I₇=0

例1．8 已知I₁=3A、I₂=5A、I₃=-18A、I₅=9A，计算图1．35所示电路中的电流I₆及I₄。

解：对节点a，根据KCL定律可知：

-I₁-I₂+I₃+I₄=0

则：I₄=I₁+I₂-I₃=（3+5+18）A=26A

对节点b，根据KCL定律可知：

-I₄-I₅-I₆=0

则：I₆=-I₄-I₅=（-26-9）A= -35A

例1．9 已知I₁=5A、I₆=3A、I₇=-8A、I₅=9A，试计算图1．36所示电路中的电流I₈。

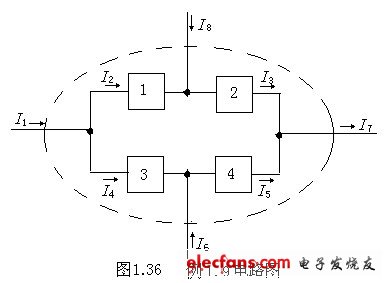
解：在电路中选取一个封闭面，如图中虚线所示，根据KCL定律可知：

-I₁-I₆+I₇-I₈=0

则：I₈= -I₁-I₆+I₇=（-5-3-8）A= -16A

1.5.2   基尔霍夫电压定律

KVL定律是描述电路中组成任一回路的各支路（或各元件）电压之间的约束关系。KVL定律指出：对电路中的任一回路，在任一瞬间，沿回路绕行方向，各段电压的代数和为零。即：

在直流的情况下，则有：

通常把式（1．21）、（1．22）称为回路电压方程，简称为KVL方程。

应当指出：在列写回路电压方程时，首先要对回路选取一个回路“绕行方向”，各电压变量前的正、负号取决于各电压的参考方向与回路“绕行方向”的关系（是相同还是相反）；而各电压值的正、负则反映了该电压的实际方向与参考方向的关系（是相同还是相反）。通常规定，对参考方向与回路“绕行方向”相同的电压取正号，同时对参考方向与回路“绕行方向”相反的电压取负号。回路“绕行方向”是任意选定的，通常在回路中以虚线表示。

例如，图1．37所示为某电路中的一个回路ABCDA，各支路的电压在选择的参考方向下为u₁、u₂、u₃、u₄，因此，在选定的回路“绕行方向”下有：

u₁+u₂-u₃-u₄=0

KVL定律不仅适用于电路中的具体回路，还可以推广应用于电路中的任一假想的回路。即在任一瞬间，沿回路绕行方向，电路中假想的回路中各段电压的代数和为零。

例如，图1．38所示为某电路中的一部分，路径a、f、c、b并未构成回路，选定图中所示的回路“绕行方向”，对假象的回路afcba列写KVL方程有：

-u₄+u₅-u_ab=0

则：u_ab=-u₄+u₅

由此可见：电路中a、b两点的电压U_ab等于以a为出发点，以b为终点的绕行方向上的任一路径上各段电压的代数和。其中，a、b可以是某一元件或一条支路的两端，也可以是电路中任意两点。今后若要计算电路中任意两点间的电压，可以直接利用这一推论。

例1．10 试求图1．39所示电路中元件3、4、5、6的电压。

解：在回路cdec中，U₅=U_cd+U_de=[-（-5）-1]V=4V

在回路bedcb中，U₃=U_be+U_ed+U_dc =[3+1+（-5）]V= -1V

在回路debad中，U₆=U_de+U_eb+U_ba=[ -1-3-4]V= -8V

在回路abea中，U₄=U_ab+U_be=（4+3）V=7V

1.5.3  支路电流法

支路电流法是以支路电流变量为未知量，利用基尔霍夫定律和欧姆定律所决定的两类约束关系，建立数目足够且相互独立的方程组，解出各支路电流，进而再根据电路有关的基本概念求解电路其它响应的一种电路分析计算方法。

为了叙述方便，首先以一个具体的例子，介绍支路电流法分析电路的全过程。

例如，图1．40所示电路有6条支路、4个节点，选定的各支路电流的参考方向均标注在图中，且各支路电流变量分别用I₁、I₂、I₃、I₄、I₅、I₆表示。

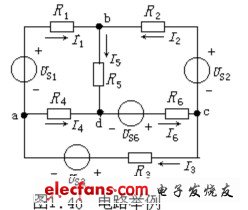
由KCL定律，可以列写出四个节点电流方程：

节点a：  I₁-I₃+I₄=0

节点b：  -I₁-I₂+I₅=0

节点c：  I₂+I₃-I₆=0

节点d：  -I₄-I₅+I₆=0

观察上述所列写的四个方程可知，它们是相互不独立的，其中任一个方程都可以从其它三个方程中推导而出，即这四个方程中只有三个方程是独立的。推而广之，对节点数为n的电路，根据KCL定律，只能列写出（n-1）个独立的节点电流方程，并将这（n-1）个节点称为一组独立节点。独立节点是任选的。

同样，由KVL定律，对电路中的每一个回路都可以列写出回路电压方程，但这些方程也不全是独立的。可以证明，如果电路的支路数为b，则独立的回路电压方程数l为：

l=b-（n-1）

而在平面电路中，网孔就是一组独立回路。

于是，在图1．40电路中，有三个网孔，即回路abda、adca、bcdb，它们是一组独立回路。由KVL定律，可以列写出独立回路电压方程：

网孔abda  -U_S1+R₁I₁+R₅I₅-R₄I₄=0

网孔dbcd  -R₅I₅-R₂I₂+U_S2-R₆I₆+U_S6=0

网孔adca  R₄I₄-U_S6+R₆I₆+R₃I₃+U_S3=0

因此，任选三个节点电流方程，加上上述三个网孔电压方程，由此就可以求解出6条支路的电流，从而可以获得电路中的其它响应。

综上所述，对于一个具有n个节点，b条支路的电路，利用支路电流法分析计算电路的一般步骤如下：

(1) 在电路中假设出各支路（b条）电流的变量，且选定其的参考方向，并标示于电路中。

(2) 根据KCL定律，列写出（n-1）个独立的节点电流方程。

(3) 根据KVL定律，列写出l=b-（n-1）个独立回路电压方程。

(4) 联立求解上述所列写的b个方程，从而求解出各支路电流变量，进而求解出电路中其它响应。

例1．11 图1．41电路中，Us₁=130V、Us₂=117V、R₁=1Ω、R₂=0.6Ω、R=24Ω，试用支路法求各支路电流。

解：这个电路的支路数b=3、节点数n=2、网孔数l=2，选定各支路电流参考方向标在图中，并设各为I₁、I₂、I。列一个节点的KCL方程和两个网孔的KVL方程：

对节点a：-I₁-I₂+I=0

对回路Ⅰ：I₁-0.6I₂= -117+130

对回路Ⅱ：0.6I₂+24I=117

解之得：I₁=10A，I₂= -5A，I=5A

例1．12 图1．42所示电路中，R₁=R₄=1Ω，R₂=2Ω，R₃=3Ω，Is = 8A，Us = 10V，计算各支路电流。

解：这个电路的支路数b=5，节点数n=3，选定各支路电流参考方向标在图中，并设各为I₁、I₂、I₃、I₄。由于电流源Is所在的支路电流等于电流源Is的电流值，且为已知量，因而应用基尔霍夫定律列出下列4个方程：

对节点a：-I₁-I₂+I₃=0

对节点b：-I₃+I₄-I_S=0

对回路Ⅰ：I₁-2I₂= -10

对回路Ⅱ：2I₂+3I₃+I₄=10

解之得：I₁= -4A，I₂=3A，I₃= -1A，I₄=7A