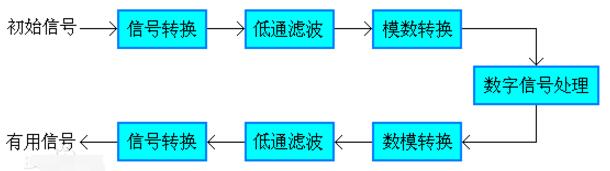
用MAXQ结合MAC进行控制和数字信号处理

用MAXQ结合MAC进行控制和数字信号处理

maxq简介

maxq系列微控制器是高性能的16位risc器件,专门为低噪声操作而设计,是用电池供电的混合信号应用的理想器件。maxq将高精度的模拟功能与数字元件集成在一起,减少了设计中的芯片数目。maxq采用harvard存储器结构,将数据、代码与寄存器空间安排在不同的总线上。这种存储器结构的主要优点是具有灵活的字长,系统与外设寄存器可以是8位或16位。由于maxq的指令字是16位的,微控制器通常具有16位指令总线。harvard结构的另一个优点是始终利用寄存器来访问存储器,这样便可以用直接存取的方式访问外设,例如模数转换器(adc)与硬件协处理器等。maxq2000是maxq系列微控制器中的第一款产品,它集成了16位cpu、64kb闪存、2kb sram和4 36字段的lcd控制器。

对控制应用和数字信号处理都有要求时出现的难题

传统微控制器(mcu)与数字信号处理器(dsp)通常被认为是微型计算机领域中两个互不兼容的机种。mcu适用于需要对非同步过程实现低延迟响应的控制应用,dsp则在高强度数学计算方面表现卓越。当然,也可以用mcu进行纷繁复杂的算术运算,但是由于绝大多数mcu的算术逻辑单元（alu）每次执行一项运算,其运算速度与dsp相比大大减慢。同理,因为内部架构的原因,dsp也不适用于控制应用。

随着在控制应用中增加少量信号处理功能的实际应用越来越多,在dsp与传统mcu之间进行选择变得越来越困难。在此类应用中,将dsp代码嵌入到mcu中的解决方法具有一定的吸引力。但是采用这种方法后,应用程序的大部分时间都花在执行dsp函数上了,而控制应用不得不有所牺牲。maxq架构的出现,解决了这个问题。在模块化的maxq架构中,可以很容易地集成乘法-累加单元(mac)。使用了硬件mac后,16 16位的乘法-累加运算可在一个周期内实现,而不影响控制处理器上的任务执行。下面举例说明如何使用maxq微控制器中的mac模块解决实际问题。

mac模块与maxq结合使用

对dsp来说,最基本的应用是对模拟信号进行滤波。在滤波应用中,将经过适当调制的模拟信号提供给adc,在数字域中对采样得到的数据流进行滤波。常规滤波器的执行过程可以用如下公式实现：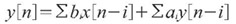

式中bi和ai分别是系统前馈与反馈响应的特征值。根据ai和bi的值,可以将数字滤波器分成有限冲击响应(fir)滤波器和无限冲击响应(iir)滤波器两大类。当系统不包含任何反馈元素时(即所有ai=0),滤波器为fir型,其方程为：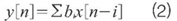

而当ai和bi的元素都不为0时,滤波器为iir型。

由公式（2）知,fir型滤波器的主要数学运算是将每个采样输入与常数相乘,然后将每个乘积累加,共进行n次,可以用如下c语言程序段来说明：

y[n]=0;
for(i=0;i小于n;i++)
y[n]+=x[i]*b[i]

对带乘法器单元的微处理器,可以根据以下伪码来实现：

move ptr0, #x ;primary data pointer -> samples
move ptr1, #b ;secondary dp -> coefficients
move ctr, #n ;loop counter gets number of samples
move result, #0 ;clear result register

acc_loop:

move acc, @ptr0 ;get a sample
mul @ptr1 ;multiply by coefficient
add result ;add to previous result
move result, acc ;...and save the result back
inc ptr0 ;point to next sample
inc ptr1 ;point to next coefficient
dec ctr ;decrement loop counter
jump nz, acc_loop ;jump if there are more samples
end

这样,尽管有一个乘法器,乘法与累加的循环也需要12条指令以及(假定是单周期运行的单元与乘法器)4+ 8n个周期。而在maxq的乘法-累加单元中完成相同的操作,代码空间从12个字缩减到9个字,运行时间从4+ 8n个周期减少到4 +5n个周期,其代码实现如下：

move dp[0], #x ; dp[0] -> x[0]
move dp[1], #b ; dp[1] -> b[0]
move lc[0], #loop_cnt ; lc[0] -> number of samples
move mcnt, #init_mac ; initialize mac unit

mac_loop:

move dp[0], dp[0] ; activate dp[0]
move ma, @dp[0]++ ; get sample into mac
move dp[1], dp[1] ; activate dp[1]
move mb, @dp[1]++ ; get coeff into mac and multiply
djnz lc[0], mac_loop

需要注意的是,在maxq乘法-累加单元中,当第二个操作数装入该单元时,请求的运算自动执行,其结果存储在mc寄存器中。还应当注意的是,在传统方法中每个基本运算后都必须进行溢出检测,而mc寄存器的长度是40位,在溢出前可以累加大量32位的乘法计算结果,这是对传统方法的改善。为了说明如何在信号处理流程中高效使用mac,现列举一个用于双音多频(dtmf)收发器的简单应用。

dtmf概述

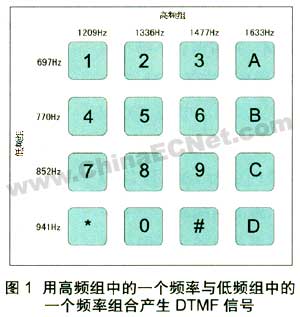
dtmf(dual tone multitre-quency)双音多频是用于电话网络中的信令技术,用来从网络终端(电话或其他设备)向交换机传送地址信息。其机理是使用两组各四路独立音调,互相之间没有谐波相关关系,例如“低频组”(低于1 khz)与“高频组”(高于1 khz)。电话键盘上的每个数字都刚好可以用一路低频组音调和一路高频组音调来表示。图1给出了这些音调的分配。

dtmf收发器的音调编码器

dtmf收发器的编码器部分简单明了,即需要两个数字正弦振荡器,每个振荡器都可以调谐到四个低频组频率或高频组频率之一。

解决数字合成正弦波问题的方法很多。

产生正弦波的方法之一是完全避免数字合成问题,只对端口引脚产生的方波进行较强的滤波。尽管这种方法在很多应用中都比较有效,但是该技术达不到bellcore（贝尔通信研究所）对正弦波频谱纯度的要求。第二种方法是利用速查表来产生正弦波。在这种方法中,将一路正弦波的1/4存储在一张rom表中,这张表根据预先计算的间隔采样来生成所需要的波形。不过,要生成一个分辨率足够高、能够满足频谱要求的1/4正弦表,需要很大的存储量,所以这种方法通常不被采用。另外一个相对较好的方法就是使用递归数字谐振器来产生正弦波。

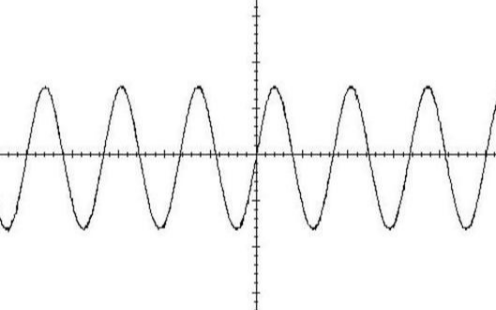
递归数字谐振器产生的正弦波如图2所示。该谐振器用双极点滤波器来实现,可用以下差分方程描述：

其中k为常数,其定义为：

由于dtmf拨号盘只需要少量音调,k的8个数值可以预先计算,并存储在rom中。例如,在8 khz的采样速率下产生行频为770 hz音调所需的常数为：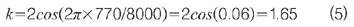

还有一个数值必须计算,即振荡器开始运行所需的初始脉冲。很明显,若xn-1与xn-2都为0,随后的每个xn都将为0。为了启动振荡器,将xn-1设置为0,并将xn-2设置为：

在本例中,假定需要单位正弦波,则（6）式可简化为：

很容易将上述过程用代码表示：初始化两个中间变量x1、 x2。x1初始化为0,而x2装入初始激励数值(以上(7)式已计算)启动振荡。执行以下操作产生正弦波的一次采样：

x0＝k*x1－x2;
x2＝x1;
x1＝x0;

每个新的正弦值都用一次乘法与一次减法来计算。使用maxq微控制器上的单周期硬件mac,正弦波可以用如下代码产生：

move dp[0], #x1 ; dp[0] -> x1
move mcnt, #init_mac ; initialize mac unit
move ma, #k ; ma=k
move mb, @dp[0]++ ; mb=x1, mc=k*x1, point to x2
move ma, #-1 ; ma=-1
move mb, @dp[0]-- ; mb=x2, mc=k*x1-x2, point to x1
nop ; wait for result
move @--dp[0], mc ; store result at x0

dtmf音调的检测

由于只需要检测少量频率,因此可以使用改进的goertzel算法。该goertzel算法比一般的dft（离散式傅立叶变换）机制更有效,并提供对频段内信号的可靠检测。图3是用简单二阶滤波器实现goertzel算法的示意图。

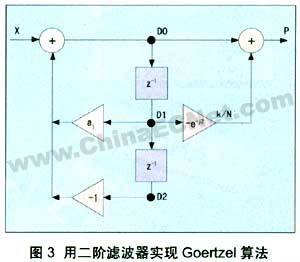
为了用goertzel算法检测特定频率的音调,必须先计算常数k。对dtmf检测器,该常数可以在编译时计算,所有的音调频率都已明确指定。k值可按公式（4）计算。

首先,将三个中间变量(d0、d1与d2)初始化为0。现在,对接收到的每个采样值x,按以下公式计算：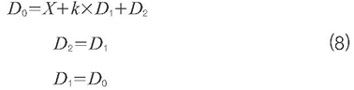

在获得了足够数量的采样值后(若采样速率为8 khz,通常为205),使用最新计算出的d1与d2计算下式：

这样p中就包含了输入信号x中测试频率的平方幂（d12与d22）。为了解码全部四列dtmf,每个采样将通过8个滤波器完成。每个滤波器将有自己的k值和一组中间变量。由于每个变量都是16位的,整个算法将需要48个字节的中间存储。

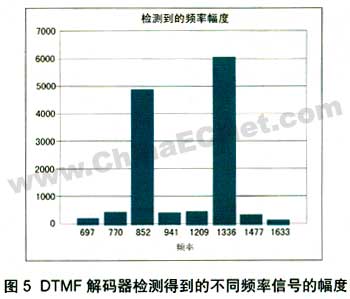
一旦计算了不同音调频率的p值,高频组与低频组中的一路音调将比其他音调的数值高出两倍以上,而通常其幅度高出一个数量级。图4是提供给解码器的采样输入信号,x的值分别为852 hz和1 336 hz。图5给出了goertzel算法的检测结果。若信号频谱达不到这个标准,有两种可能情况,要么是信号中没有dtmf能量,要么是噪声太大阻断了信号。

说明该算法的电子表格以及配备了mac的maxq处理器的实例代码在网站www.maxim-ic.com/maxq_dtmf上有说明。

结论

maxq微控制器与其mac单元相结合,在传统mcu与dsp之间架起了桥梁,很好地解决了控制应用与需要少量信号处理并存系统的技术问题。添加了硬件mac之后,maxq微控制器将过去16位微控制器的信号处理能力提高到了新水平。单周期的mac还提供了常用函数,使实时信号处理成为可能。