高速高分辨率ADC电路设计及信噪比分析

在雷达、导航等军事领域中，由于信号带宽宽(有时可能高于10MHz)，要求ADC的采样率高于30MSPS，分辨率大于10位。目前高速高分辨率ADC器件在采样率高于10MSPS时，量化位数可达14位，但实际分辨率受器件自身误差和电路噪声的影响很大。在数字通信、数字仪表、软件无线电等领域中应用的高速ADC电路，在输入信号低于1MHz时，实际分辨率可达10位，但随输入信号频率的增加下降很快，不能满足军事领域的使用要求。

针对这一问题，本文主要研究在不采用过采样、数字滤波和增益自动控制等技术条件下，如何提高高速高分辨率ADC电路的实际分辨率，使其最大限度地接近ADC器件自身的实际分辨率，即最大限度地提高ADC电路的信噪比。为此，本文首先从理论上分析了影响ADC信噪比的因素；然后从电路设计和器件选择两方面出发，设计了高速高分辨率ADC电路。经实测表明，当输入信号频率为0．96MHz时，该电路的实际分辨率为11．36位；当输入信号频率为14．71MHz日寸，该电路的实际分辨率为10．88位。

1 影响ADC信噪比因素的理论分析

ADC的实际分辨率是用有效位数ENOB标称的。不考虑过采样，当满量程单频理想正弦波输入时，实际分辨率可用下式表示：

ENOB=[SINA0(dB)-1．76]／6．02 (1)

式中，SINAD表示ADC的信噪失真比，指ADC满量程单频理想正弦波输入信号的有效值与ADC输出信号的奈奎斯特带宽内的全部其它频率分量(包括谐波分量，但不包括直流允量)的总有效值之比。

ADC的信噪比SNR，指ADC满量程单频理想正弦波输入信号的有效值与ADC输出信号的奈奎斯特带宽内的全部其它频率分量(不包括直流分量和谐波分量)总有效值之比。

由此可知，当ADC的总谐波失真THD一定时，有效位数ENOB取决于SNR；ADC的SNR越高，其有效位数ENOB就越高。下面就来分析影响ADC信噪比SNR的因素。

理想ADC的噪声由其固有的量化误差(也称为量化噪声，如图1所示)产生。但实际使用的ADC是非理想器件，它的实际转换曲线与理想转换曲线之间存在偏差，表现为多种误差，如零点误差、满度误差、增益误差、积分非线性误差INL、微分非线性误差DNL等。其中，零点误差、满度误差、增益误差是恒定误差，只影响ADC的绝对精度，不影响ADC的SNR。INL指的是在校准上述恒定误差的基础上，ADC实际转换曲线与理想转换曲线的最大偏差。而DNL指的是ADC实际量化间隔与理想量化间隔的最大偏差，改变ADC的量化误差，能更直接地计算出ADC实际转换曲线与理想转换曲线的偏差对ADC的SNR的影响。



非理想ADC，除了上述误差外，还有各种噪声，如热噪声、孔径抖动。前者是由半导体器件内部分子热运动产生的，后者是由ADC孔径延时的不确定性造成的。而ADC的外围电路同样会带来噪声，如ADC输入级电路的热噪声、电源／地线上的杂波、空间电磁波干扰、外接时钟的不稳定性(导致ADC各采样时钟沿出现时刻不确定，带来孔径抖动)等，可以把它们都等效为ADC的上述两种内部噪声。

上述误差和噪声的存在，导致ADC的SNR下降。下面先给出理想ADC的SNR计算公式，然后具体分析微分非线性误差DNL、孔径抖动△tj和热噪声对ADC的SNR的影响。

1．1 理想ADC的SNR

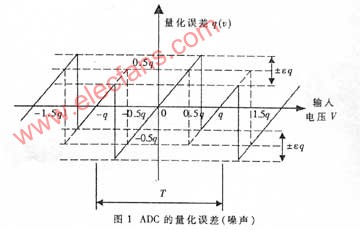
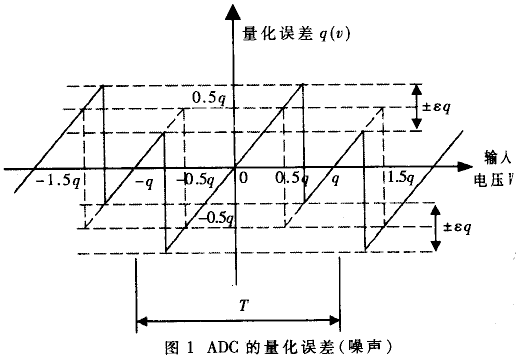
理想ADC的量化误差g(υ)与满量程内输入信号的电压V的关系如图1所示。量化误差为在[-q/2，q/2]内均匀分布且峰-峰值等于q(q=1LSB，LSB表示理想ADC的最小量化间隔)的锯齿波信号。

设N位ADC满量程电压为±1V，输入信号为s(t)=sinωt，则输入信号电压有效值Vs=1/√2=2N/2√2×q，量化噪声电压有效值于是得ADC输出信噪比为

SNR=6．02N+1．76(dB)

1．2 微分非线性误差DNL

非理想ADC的量化间隔是非等宽的，这将导致ADC器件不能完全正确地把模拟信号转化成相应的二进制码，从而造成SNR的下降；且ADC每个量化的二进制码所对应的量化间隔都不同，为便于分析，用ε(LSB)= εq表示实际量化间隔与理想量化间隔误差的有效值，并近似认为由于DNL的影响，在无失码条件(DNL<1LSB)下，量化误差均匀分布在[-上q+εq/2，q+εq/2]和[-q－εq/2，q－εq/2]内。如图1 中实线所示（虚线伪理想ADC量化误差）。这样，在考虑了DNL之后的ADC量化噪声电压Vq_DNL为：



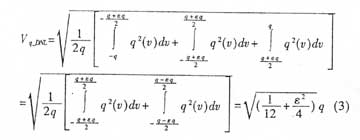
1．3 孔径抖动△tj

孔径时间又称孔径延迟时间，是指对ADC发出采样命令(采样时钟边沿)时刻与实际开始采样时刻之间的时间间隔。相邻两次采样的孔径时间的偏差称为孔径抖动，记作△tj。孔径抖动造成了信号的非均匀采样，引起了误差，设ADC满量程电压为±1V输入信号为s(t)=sinωt，孔径抖动有效值为σ△tj，则由孔径抖动带来的误差电压为：



1．4 热噪声

这里将ADC电路中微分非线性误差DNL、孔径抖动△tj外的其它噪声都等效为ADC输入端的热噪声电压Vtn，设其有效值为σtn。

1．5 非理想ADC的SNR

一般情况下，量化噪声、微分非线性误差DNL、孔径抖动△tj和热噪声彼此相互独立，综合芍虑这四个因素的影响，可得到ADC的SNR计算公式如卡：



式中，N--ADC的量化位数

ε--ADC的实际量化间隔与理想量化间隔误差的有效值，单位LSB
fin--ADC输入信号频率，单位Hz
σ△tj--ADC的孑L径抖动有效值，单位s
σtn--等效到ADC输入端的热噪声的有效值单位LSB

对于高分辨率ADC器件，其固有量化误差、微分非线性误差DNL和器件热噪声均较小。当fin较高时，ADC电路的SNR主要取决于孔径抖动，此时有



2 基于AD6644AST一65的高速高分辨率ADC电路设计实例

电路设计目标：有效位数ENOB≥10．50bit、采样率为40MSPS、输入信号频率小于15MHz，输入信号幅度为-ldBFs。该指标能满足数字仪表、高速数据采集卡、软件无线电和雷达、导航等领域中数字波束形成的要求。

2．1 电路设计与器件选择

本电路主要由模／数转换器ADC、输入电路、输出屯路、时钟电路和电源电路组成，如图2所示。



2．1．1 时钟电路

时钟电路的设计主要包括AD6644AST-65采样时钟相位噪声指标的确定以及PECL差分时钟的实现。

ADC电路的孔径抖动有效值σ△tj，包括ADC器件自

2．1．2 ADC输入电路

ADC输入电路多采用运放直流耦合或变压器交流耦合方式，为输入信号提供增益、偏置和缓冲。

由于运放为有源器件，除具有一定的谐波失真外，还存在主要集中在低频段的1／f噪声和较宽频带内的白噪声。这些噪声和谐波失真都降低了运放的信噪比SNR和有效位数ENOB。当运放的SNR不明显优于甚至低于ADC的SNR时，它带来的噪声是不容忽视的，对于高分辨率ADC电路，甚至是不能接受的。而作为无源器件的变压器，一般认为它的噪声和谐波失真是微乎其微、可以忽略的。因此，本电路的输入电路采用变压器交流耦合方式，选用Mini-Circuits公司的变压器T4-6T。

为进行比较，同时也提供运放直流耦合方式，采用ADI公司的低噪运放AD8138。根据AD8138的关参数，计算得到的AD8138输出的总谐波失真和热噪声之和大于1LSB。该指标可能导致无法满足电路热噪声不大于1．50LSB的设计要求，并带来更大的谐波失真。因此可预知，采用AD8138时，ADC电路的有效位数ENOB会比采用变压器时的有效位数ENOB有所下降，甚至达不到设计要求。

2．1．3 ADC输出电路

ADC的模拟输入和数据输出之间存在少量的寄生电容，ADC数据输出线上的噪声会通过这些寄生电容耦合到模拟输入端，导致ADC的SNR和有效位数ENOB下降。为解决这一问题，可在ADC数据输出端接一锁存器。

为减小ADC电源的波动，应尽量降低ADC输出端的负载电容和输出电流。在ADC数据输出端接一锁存器可避免将其直接连在数据总线上，有效限制了其输出端的负载电容；在ADC每一个数据输出端都串联一个电阻，可限制其输出电流。

本电路采用74LC574作为AD6644AST-65的输出数据锁存器，同时每一个数据输出端都串联一个100Ω的电阻。

2．1．4 电源、地和去耦电路

AD6644AST-65的电源抑制比PSRR≈±lmV／V，当外接电源的纹波为峰-峰值100mV时，等效于在AD6644AST-65输入端产生100μV(0．77LSB)大小的噪声，这相对于设计指标而言是不能接受的。为减小外接电源对电路的影响，本电路采用Linear公司的低压差LDO线性稳压器LTl086-5和LTlll7-3．3(两个芯片的PSRR均大于60dB) 对外接稳压电源进行稳压，为AD6644AST-65等模拟电路提供5V电源和3．3V电源。

时钟、ADC的输出信号以及后级数字电路的数字信号的跳变都会引起电源电流的急剧变化，由于印刷电路板的电源线和地线上存在分布电阻、电容和电感，当有变化的电流经过时，其上的压降也随之变化；频率较高时，就表现为电地间的高频杂波。为降低这类杂波干扰，本电路采取以下措施：

· 时钟电路的5V电源，由VCC_5VA串联一磁珠FB得到；
· AD6644AST-65后级数字电路的3．3V电源，由VCC_3．3VA串联一磁珠FB得到；
· 模拟地和数字地分开布线，并在一点用磁珠FB相连；
· ADC的所有电源管脚都就近对地接去耦电容。

磁珠对MHz级以上的信号有较好的吸收作用，能有效降低时钟电源、数字电源对AD6644AST-65模拟电源的影响，以及数字地对模拟地的影响。

去耦对于高速高分辨率ADC电路尤为重要。为此，本电路采用0．01μF的NPO材料(属低损耗、超稳定的电容材料，电气特性基本上不随温度、电压、时间的变化而变化，自谐振频率较高，适用于高频场合)自0 1206封装的贴片电容和0．1μF的X7R材料(属稳定性电容材料，电气特性随温度、电压、时间变化不明显，适用于中、低频场合)的0805封装的贴片电容并联，有效地滤除电地间较宽频带的杂波。

2．1．5 电路板的布局布线

ADC界于模拟电路和数字电路之间，且通常被划归为模拟电路。为减小数字电路的干扰，应将模拟电路和数字电路分开布局；为减小信号线上的分布电阻、电容和电感，应尽量缩短导线长度和增大导线之间的距离；为减小电源线和地线的阻抗，应尽量增大电源线和地线的宽度，或采用电源平面、地平面。本电路在设计印刷电路板时，都遵循了以上原则。

2．2 电路测试结果

采用信号发生器HP8640B产生0~15MHz的单频正弦信号，经相应带通滤波器滤波(各次谐波均小于-90dBc)后作为本电路的输入信号，滤波后信号在AD6644AST-65输入端幅度为-ldBFs。

AD6644AST-65输出数字信号经74LC574锁存后，存储于逻辑分析仪HPl6702A中。HPl6702A状态分析时钟取自AD6644AST-65的DRY管脚，该信号频率和AD6644AST-65采样时钟频率一致，为40MHz。

通过对逻辑分析仪HPl6702A每次存储的数字信号进行16384点FFT分析，可得到奈奎斯特带宽内总功率PΣ、输入信号功率只以及总谐波失真与噪声功率之和Pn+THD=PΣ-Ps。经计算得到电路的有效位数ENOB=[SINAD(dB)-1．76]／6．02=[Ps (dB)-Pn+THD (dB)-1．76]／6．02。

图3(a)、(b)、(c)为在三种不同测试条件下，AD6644AST-65输出数字信号的FFT分析频谱图和有效位数ENOB。

图3(c)表明，当fin=0．96MHz、AD6644AST-65输入端采用运放AD8138直流耦合时，电路热噪声和谐波失真明显增加，电路的有效位数ENOB约为10．74bit，比图3(a)的ENOB小0．6bit左右。由此可见，有源器件对高速高分辨率ADC电路性能的影响是很大的。



理论分析和实际电路的测试结果都说明，高速高分辨率ADC电路设计应选用低噪器件；当输入信号频率较高时，应选用低相位抖动的时钟源；在进行电路扳布局布线时，应注意电源噪声的抑制和减小数字电路对模拟电路的影响。