三相PFC整流器在输入电压不对称时的改进 - 全文

　　1 引言

　　三相 PFC 整流器的控制主要有半解耦和全解耦两大类，主流的控制算法有基于 d-q 解耦的空间矢量调制，迟滞比较算法和单周期控制等。空间矢量调制要求对输入电压进行d-q 解耦控制算法复杂，需采用数字信号处理器DSP 才能实现。而迟滞比较算法的开关频率不恒定，对输入和输出的干扰比较大，需要比较大的电感和电容作为滤波元件。

　　分析了基于单周期控制技术的双并联升压型三相 PFC 整流器在电网电压不对称时输入电流跟踪输入电压不良的问题，提出了一种有效的改进措施，通过计算相电压不对称系数，对占空比计算公式进行修正，以消除不对称电压对输入电流波形跟踪不良的影响，使每相电流均和各自的电压同相，从而实现单位功率因数和低电流畸变。在任意时刻，该整流器只需要两个开关管工作在高频状态，从而使开关管的总体损耗程度进一步降低。最后通过硬件实验验证了该控制策略的正确性。

　　2 系统结构和状态方程

　　图 1 给出了双并联升压型三相整流器的主电路原理图。另外，图2 还给出了输入电压b 相幅值减少20% ,c 相相位滞后30 °时三相电压的波形，并按虚线划分为六个区间。须注意的是，输入电压不对称的情况不同，其分区点也可能不同，分区点由各相非零序电压瞬时最大幅度区分点所确定。依据六阶段PWM 控制技术原理，三相整流器可以通过在线性周期的每一区间内控制两个开关的通断来实现单位功率因数。

　　

 

　　图1 双并联升压型三相整流器主电路拓扑图

　　

 

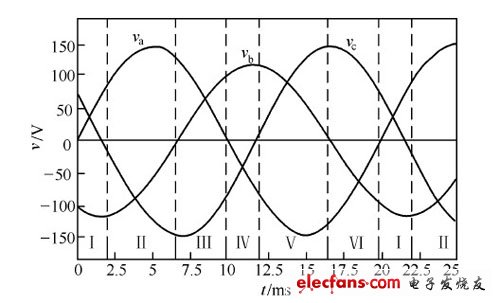
　　图2 b相幅值减小20% ，c相滞后30 ° 时三相电压的波形图

　　在开始详细分析前，假设输入电压为正弦波，三相电路参数对称，功率元器件的正向阻抗和其他寄生参数忽略不计。以图1 的主电路输入如图2 所示的电压为例，在区间I 内，开关Sb 一直处于导通状态，只对开关Sa 和Sc 进行控制，此时三相整流器可以解耦为如图3 所示的双并联升压型拓扑结构。

　　图中 Vp 、Vn 为不同区间所对应的电压，Lp、 Ln 和Lt 为不同区间所对应的电感，Tp、 Tn 为不同区间所对应的主控开关，dp 、dn 为主控开关的占空比。由于PWM 开关频率远高于电网频率，因此，在一个开关周期内，各电感的电压平均值为零，运用回路电流法和节点电压法对各种开关状态进行分，析可得出：

　　

 

　　和

　　

 

　　从而推导出

　　

 

　　其中

　　

 

　　可以证明，式1 在任意区间的两种开关顺序都成立，并且只要电路工作在连续导通的模式，该等式即能准确反映出稳态电路的输入电压、输出电压和占空比三者之间的固定关系，与所采用的控制方案无关。因此式1 即为该整流器的状态方程。

　　3 不对称电压对输入电流的影响

　　文献[1]依据式4 构建三相PFC 整流器，并根据三相电压对称和实现单位功率因数的目标而令va = Reia ，vb = Reib和vc = Reic,然后根据va+vb+vc=0和ia+ib+ic=0 的约束条件得知只要控制其中两相电流跟踪对应相的电压，就可以使另外一相电流也跟踪该相电压。由此推算出实现单位功率因数的占空比计算公式：

　　

 

　　当输入电压不对称时，va+vb+vc=0 不一定成立，如果仍然按照式5 作为单周期控制的占空比函数，此时各相电流为：

　　

 

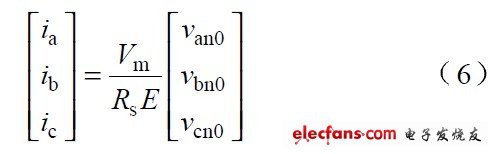
　　其中：

　　

 

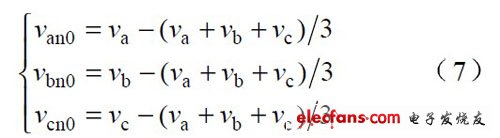
　　即 van0, vbn0 和vcn0 分别为各相电压不含零序电压的部分。由式(6) 和式(7 )可知，各相电流仍能保持低电流畸变。但若(va+vb+vc)/3≠0, 输入电流和输入电压会存在一个相位差，从而导致系统不能实现单位功率因数。为使系统仍能实现单位功率因数的目标，必须改进系统的控制策略。

　　4 改进的控制策略

　　4.1 相电压不对称系数的计算

　　三相输入电压不对称时，假设各相电流跟踪各自的相电压此，时可令从输入端看进去各相对中线的等效电阻为Ra ，Rb 和Rc 。因系统采用三相三线制在任意时刻均有：

　　

 

　　故对任意时刻 t0 t1 t2, ……，tn 有：

　　

 

　　由于电网电压可能存在各种干扰，为使计算结果尽可能精确，可将一个或几个周期内的n 个采样电压分为多组，取其中的两组来计算相电压不对称系数。对式(9) 按该两组相加，可得：

　　

 

　　由此得：

　　

 

　　式 (11 )为相电压不对称系数的计算公式，其中λa ,λb 和λc 为相电压不对称系数，Re 为标准等效电阻。可见，当电网电压不对称时，为使各相电流仍能正确跟踪对应相电压，各相等效电阻值是不同的。特殊地，如果三相电压对称，λa=λb=λc =1 ,则Ra=Rb=Rc=Re.

　　4.2 PFC 控制策略

　　由于三相输入电压不对称，为达到单位功率因数，可令各相电流都跟踪各自相电压，即：

　　

 

　　根据式 (3 )，以区间I 为例，可以通过控制开关 Tp 、Tn 使电感电流iLb iLc 对应 V *p和 V *n相应的变化来实现。由于在I 区间内有：

　　

 

　　把式(8 )式(11 )和式(12 )代入式(13) 得：

　　

 

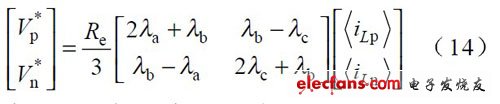
　　把式(14 )代入式(3 )得：

　　

 

　　令：

　　

 

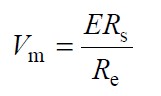
　　式中--Rs 等效电流监测电阻。

　　Vm --反馈电压环误差补偿器的输出电压。

　　此时式(15 )可表示为：

　　

 

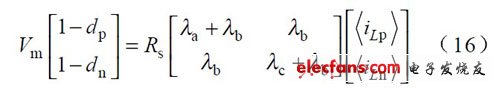
　　采用相同的分析方法所有区间内的占空比公式可统一表示成：

　　

 

　　其中矩阵 T 在不同区间的取值如表1。

　　表 1 矩阵 T 在不同区间的取值对照表

　　

 

　　由式(17 )可知，如果控制开关Tp 和Tn, 使开关占空比dp 和dn 满足该式的线性组合，就可以实现三相PFC. 因此，式(17 )是改进后实现单位功率因数的关键函数。当输入电压对称时，λa=λb=λc=1 ,式(17 )即简化为式(5)。

　　4.3 改进策略条件下各相电流幅值分配比例

　　以下详细分析按改进策略控制整流器时各相电流幅值分配比例的情况。不失一般性，假设三相输入电压为：

　　

 

　　由于改进策略的控制目标为各相输入电流跟踪对应相电压，因而各相输入电流可表示成：

　　

 

　　将式(19 )代入式(8 )可得：

　　

 

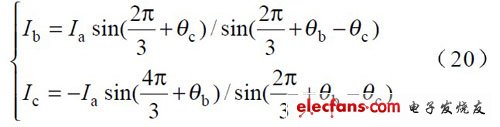
　　由式(20 )可得出以下三点结论：①各相电流幅值的分配比例只与输入相电压的偏移角度有关，与各相输入电压的幅值大小无关。并且在一定范围内，偏移角度越大，该相的电流幅值分配比例就越大。②若输入相电压相位对称，即θb=θc=0 ,输入相电流对称。③输入缺相时，由于所缺相的电流必为0 ,由式(8 )和式(20 )可知，其他两相的电流也必为0 .此时，整流器不能正常工作。

　　5 实验研究

　　为验证以上理论分析的正确性，根据图1 所示的主电路拓扑结构搭建一个2kW 的三相PFC 实验系统。该实验系统采用TI 公司的TMS 320LF2407为整个系统的核心控制模块，实现区间判定、相电压不对称系数计算、占空比计算、PWM 调制等控制功能。系统的主要参数为：输入电感La=Lb=Lc=10mH ,输出电容C0=470μF ,主开关元件采用MTY25N60E, 整流二极管采用MUR3080 ;系统的输出为直流400V ;开关频率为5kHz ;负载电阻为;输出功率为1.6kW ;实验的输入电流和a 相电压如图4 所示，示波器电压波形为50V/格，电流波形为 5A/格;图4a、 图4b 的时间t 为4ms/格;图4d的时间t 为100ms/格，对比图4 电流波形可以发现：

　　

 

　　

 

　　

 

　　

 

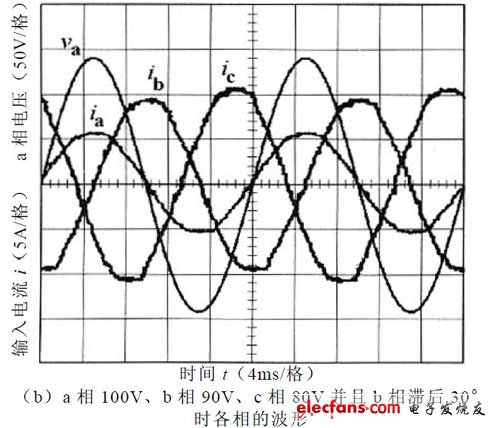
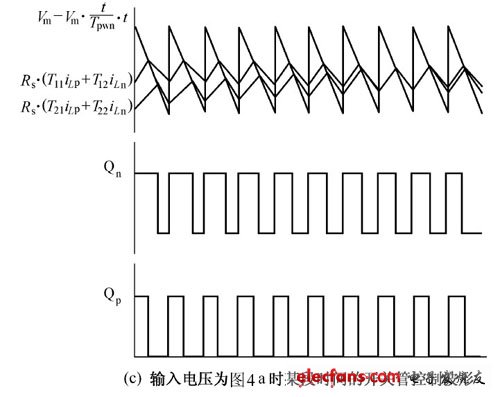
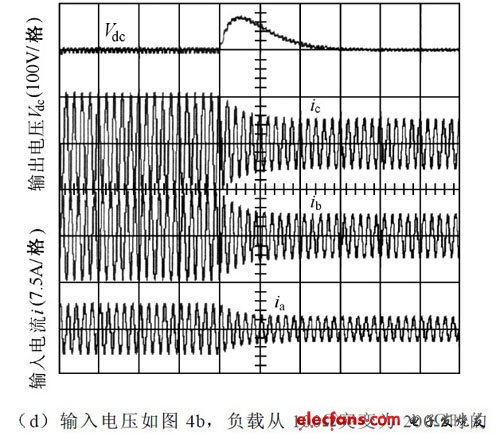
　　图4 实验输入电压电流波形图

　　①只要三相电压相位对称，输入电流就对称。②相位不对称时，各相的电流幅值差别就比较大。③文献[1]所提出的单位功率因数控制方法在输入电压不对称时输入电流会发生相移，实现不了单位功率因数。④从图4d 可以看出系统动态响应时间约为4 个电源周期，这和采用文献[1]算法的系统动态响应时间大致相当。对图4a 和图4b 的各电流波形进行傅里叶分析，各相的THD 均在3%以下，功率因数为99.98%左右，进一步验证了改进控制策略的正确性在输入对称或不对称情况下，各相电流都能很好地跟踪相电压，实现了单位功率因数。

　　6 结论

　　与其他类型的三相PFC 整流器比较起来，本控制器有工作可靠、控制方案简单、只需要进行简单运算等优点，并且在输入电压不对称的情况下仍能实现单位功率因数和很低的电流畸变。随着DSP 技术和工艺的迅猛发展，高性能DSP 硬件成本越来越低，采用高性能DSP 实现本控制器，其电路复杂度将大大降低，具有良好的应用前景。