50%以上占空比脉宽调制 (PWM) 降压转换器的电流模式控制 (CMC)可能会进入次谐波振荡。Lloyd H Dixon 在《参考文献 1》中对此做了详细的论述。Dixon表示,这种解决方案给电流检测信号增加一个斜率,其等于输出电感电流的下斜率。需将该额外电压加入要求计算过程中,以便选择正确的电流检测电阻器。
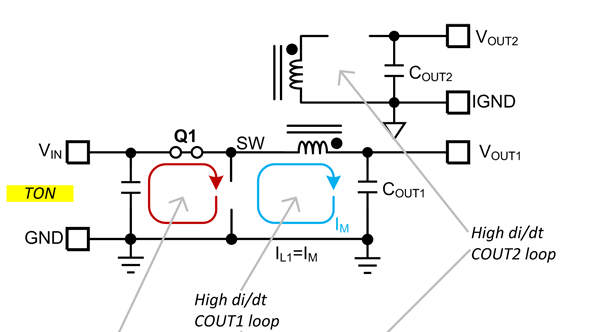
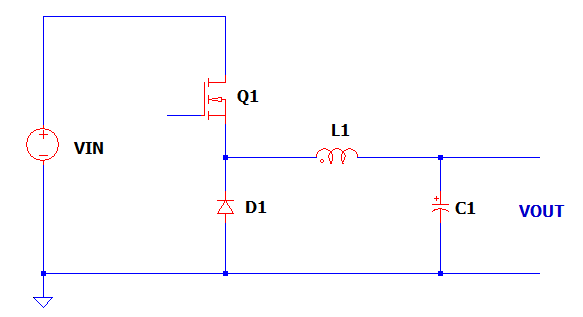
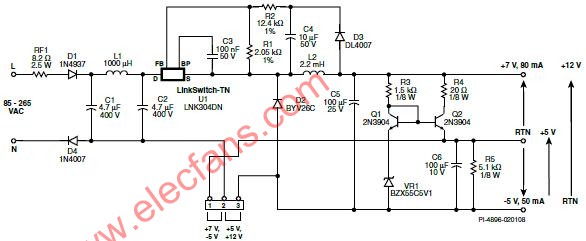
输出电感占空比大于 50% 的推挽式转换器、相移全桥转换器或者任何正向转换器,都是一些需要这种补偿的拓扑结构。但是,为了方便演示,本文选择的拓扑是一种人们相对不熟悉的拓扑结构:三开关正向转换器。请参见图 1 所示电源部分基本原理图。尽管这种拓扑的专利权归 TI 所有,但电路中使用 TI 控制 IC 时都可以使用。
图 1 三开关正向拓扑

这种拓扑拥有许多优点,特别是输入电压范围为手机电池的 36 到 72 V 时。拓扑的最大占空比为 67%,从而将设计限定在 67% 最小输入电压时的最大占空比。与此同时,关闭时主开关的电压被限定为电源轨输入电压。这就意味着,低压FET会与其相应低 RDS(on) 电阻一起使用。这种拓扑还提供了一种恢复电源变压器和主侧漏电感中磁能的方法,从而不再需要高损耗的缓冲器。
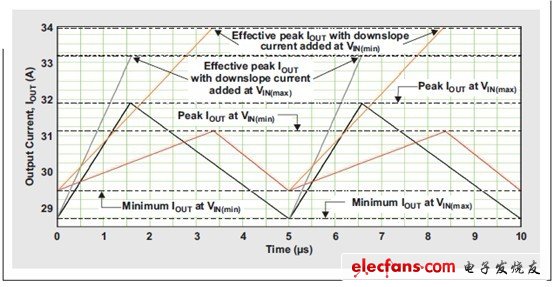
图 2 VIN(min)和VIN(max) 的最大负载输出电感纹波

这种转换器设计在许多其他方面都与降压拓扑结构一样,但是占空比必须限定在67%,以避免出现变压器饱和。通过选择一个具有编程最大占空比的控制IC(例如:UCC2807-1等),可以实现这种限制(见《参考文献 2》)。由于这种控制器具有要求的占空比限制功能,因此它是这种应用的首选。所以,本文使用了这种控制器,利用其各种特性进行分析。
下面的分析均假设有一个 100W、3.3V 输出的理论开关电源。该电源流过输出电感的最大峰值到峰值纹波电流等于 30A 最大输出 DC 负载电流的 10%,而输入电压范围为 36V 到 78V 之间。另外,我们还假设 0.5V 正向压降 Vfd 的同步整流器用于输出。第一步是确定变压器的匝数比。最小输入电压时,占空比处在最大极限 (67%)。利用下列方程式可计算出变压器输出端需要的电压。

如果假设变压器一次绕组电压为 36V,则匝数比 (Np) 为 6.147,因此会使用 6匝的一次绕组。一次绕组被分成两部分,每部分 3 匝(参见图 1)。标准方法是,把二次绕组夹在两个分拆开的一次绕组之间,Q3 也放置在它们两个之间。输入为 78V 时,变压器输出电压为 12.3V,从而得到约 31% 的最小占空比 Dmin。因此,最大“关闭”时间等于
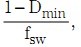
其中,fsw 为 200kHz 的计划开关频率。达到 10% 理想峰值到峰值纹波电流的最小输出电感(图 1 所示 L1)为:

通过计算得到,方程式 2 中输出电感为 4.33 µH。为了设计方便,我们使用 4.5 µH。使用该值以后,可以计算得到输出电感的下降电流 Ids 为:

通过计算得到,电感的下降电流 (Ids) 为 0.844 A/µs。
同时还得到,最大输入电压时输出电感的峰值电流为:

由于最大峰值到峰值纹波电流被定义为 10% 输出电流,该电流经过平衡后得到额定 DC 输出。所得峰值电流为 31.884 A。
最小输入电压时,确定 LOUT 的差动电压是可能的。由此,我们可以知道输出电感的变化速率为 0.489 A/µs。知道占空比和频率后,便可以计算出输出电感中电流增加的时间,从而能够确定这些状态下的纹波电流大小。最后,我们可以知道最小输入电压下的峰值电流为 31.122 A。具体波形显示在图 2 中。这些值几乎都相等,但如果增加下降电流,它们便会变化—以一种令人吃惊的方式。为了获得最大输入电压必须给峰值电流增加的下降电流为:

为了获得最小输入电压而必须给峰值电流增加的下降电流为:
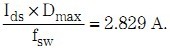
请参见图 3,其有效下降电流被添加至图2所示电流。结果,即使实际峰值相反,但最小输入电压的有效峰值电流还是高于最大输入电压的有效峰值电流。有效最大电流(包括最小输入电压的下降电流)的峰值为33.9A,其为设置电流检测电阻器Rs必须使用的值。该电流(包括转变为一次电流的下降电流)为5.658A。
选作控制器的IC拥有1.0V的典型电流自动切断电平,但容差值在0.9到1.1V之间。要确保所有单元都能提供要求的功率,需使用下限,并设定Rs值,以便让5.658A时它的电压为0.9V最小值的95%。这样便可实现5%的瞬态安全余量,并将Rs设定在0.15Ω。当然,会有5W左右的功率损耗,其最有可能由一个电流变压器产生。使用一个100:1的变压器时,Rs可能会增加至15Ω。后面内容,我们假设使用这样一个变压器。
图 3 二次电流加有效下降电流
实际上,下降电流(Ids)既没有流过电流变压器,也没有流过电源变压器,但却需要考虑其影响,它会影响电阻器Rs的电压。因此,需在电阻器Rs和IC的电流检测引脚之间增加一个电阻器Rdspri。在IC的电流检测引脚处,电流斜波被注入到电路中。这种电流斜波的存在,让IC电流检测引脚和电阻器Rs之间电阻器Rdspri中形成的等变电压(ramp voltage),等于Ids转变为一次电流在电阻器Rs中形成的电压。我们假设,一个等效下降电流正流经电阻器Rs,从而同时考虑到电源变压器和电流变压器绕组比。这种情况下,为了计算简单,我们将电阻器Rdspri设定为1kΩ,其远大于电阻器Rs。
接下来,计算Rdspri要求的dv/dt:

由该结果,我们可以计算得到1kΩ电阻器需要的电流斜波:

最大“开”时间的这种电流带来70.7 µA的峰值电流。
使用一个可编程、最大占空比 PWM 控制器(例如:UCC2807)时,通过将两个计时电阻器设定为相同值来将最大占空比设定为67%相对更加简单,如产品说明书所示。另外,这种组件的规格额定,计时电容器的谷值电压和峰值电压分别等于1/3VCC 和 2/3VCC。这样便得到一个 1/3VCC 的电压斜波幅值。知道这一点以后,我们现在便可以对电路进行设计,让它产生一个可注入到电流检测电路中的斜波电流,以向电流信号提供下降电流。
图 4 显示了用于产生期望电流的一个电路。该电路基于 UCC2807-1 控制 IC,VDD 设定为 11V。“三角”斜波的谷值电压和峰值电压为 3.667V 最小值和 7.33V 最大值,并且最小值到最大值的时间等于最大“开”时间。在该电路中,R3 等于 2 倍 R4。这样便让 Q6 基极的电压等于 1/3VCC,其为“三角”电压的谷值。由于“三角”引脚的电压在谷值到峰值(2/3VCC)之间摆动,R2 的电压便在 0 到 1/3VCC 之间线性变化。给 R2 选择一个值,让其获得 70.7 µA 的电流和 3.667 V 的 (51.8 kΩ) 电压,然后使用 Q5/R1 和 Q7/R6 构建起统一电流反射镜。这样,设计人员便可以生成电流检测信号,将所需电流加至电流检测信号,并拥有正确的形态和 1Kω 电阻计时。
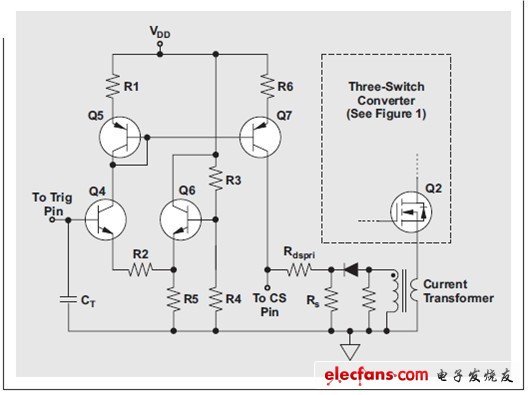
图 4 用于生成预期 Rdspri 电流的电路
结论
三开关正向转换器在能量回收方面拥有许多独到之处,它可以将磁能和一次侧漏能量返回至源,无需使用缓冲器,降低了普通正向转换器中常见的电磁干扰。相比占空比大于50%的双开关正向拓扑结构,它同样具有许多优势。本文为您介绍了一个计算举例。在确定电流检测电阻器值,以及了解降压转换器50%以上占空比稳定工作所需下降电流的影响时,这种计算都是必需的。文章还介绍了增加转换器下降电流的一种方法。
输出电感占空比大于 50% 的推挽式转换器、相移全桥转换器或者任何正向转换器,都是一些需要这种补偿的拓扑结构。但是,为了方便演示,本文选择的拓扑是一种人们相对不熟悉的拓扑结构:三开关正向转换器。请参见图 1 所示电源部分基本原理图。尽管这种拓扑的专利权归 TI 所有,但电路中使用 TI 控制 IC 时都可以使用。
图 1 三开关正向拓扑

这种拓扑拥有许多优点,特别是输入电压范围为手机电池的 36 到 72 V 时。拓扑的最大占空比为 67%,从而将设计限定在 67% 最小输入电压时的最大占空比。与此同时,关闭时主开关的电压被限定为电源轨输入电压。这就意味着,低压FET会与其相应低 RDS(on) 电阻一起使用。这种拓扑还提供了一种恢复电源变压器和主侧漏电感中磁能的方法,从而不再需要高损耗的缓冲器。
图 2 VIN(min)和VIN(max) 的最大负载输出电感纹波

这种转换器设计在许多其他方面都与降压拓扑结构一样,但是占空比必须限定在67%,以避免出现变压器饱和。通过选择一个具有编程最大占空比的控制IC(例如:UCC2807-1等),可以实现这种限制(见《参考文献 2》)。由于这种控制器具有要求的占空比限制功能,因此它是这种应用的首选。所以,本文使用了这种控制器,利用其各种特性进行分析。
下面的分析均假设有一个 100W、3.3V 输出的理论开关电源。该电源流过输出电感的最大峰值到峰值纹波电流等于 30A 最大输出 DC 负载电流的 10%,而输入电压范围为 36V 到 78V 之间。另外,我们还假设 0.5V 正向压降 Vfd 的同步整流器用于输出。第一步是确定变压器的匝数比。最小输入电压时,占空比处在最大极限 (67%)。利用下列方程式可计算出变压器输出端需要的电压。

如果假设变压器一次绕组电压为 36V,则匝数比 (Np) 为 6.147,因此会使用 6匝的一次绕组。一次绕组被分成两部分,每部分 3 匝(参见图 1)。标准方法是,把二次绕组夹在两个分拆开的一次绕组之间,Q3 也放置在它们两个之间。输入为 78V 时,变压器输出电压为 12.3V,从而得到约 31% 的最小占空比 Dmin。因此,最大“关闭”时间等于
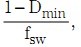
其中,fsw 为 200kHz 的计划开关频率。达到 10% 理想峰值到峰值纹波电流的最小输出电感(图 1 所示 L1)为:

通过计算得到,方程式 2 中输出电感为 4.33 µH。为了设计方便,我们使用 4.5 µH。使用该值以后,可以计算得到输出电感的下降电流 Ids 为:

通过计算得到,电感的下降电流 (Ids) 为 0.844 A/µs。
同时还得到,最大输入电压时输出电感的峰值电流为:

由于最大峰值到峰值纹波电流被定义为 10% 输出电流,该电流经过平衡后得到额定 DC 输出。所得峰值电流为 31.884 A。
最小输入电压时,确定 LOUT 的差动电压是可能的。由此,我们可以知道输出电感的变化速率为 0.489 A/µs。知道占空比和频率后,便可以计算出输出电感中电流增加的时间,从而能够确定这些状态下的纹波电流大小。最后,我们可以知道最小输入电压下的峰值电流为 31.122 A。具体波形显示在图 2 中。这些值几乎都相等,但如果增加下降电流,它们便会变化—以一种令人吃惊的方式。为了获得最大输入电压必须给峰值电流增加的下降电流为:

为了获得最小输入电压而必须给峰值电流增加的下降电流为:
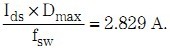
请参见图 3,其有效下降电流被添加至图2所示电流。结果,即使实际峰值相反,但最小输入电压的有效峰值电流还是高于最大输入电压的有效峰值电流。有效最大电流(包括最小输入电压的下降电流)的峰值为33.9A,其为设置电流检测电阻器Rs必须使用的值。该电流(包括转变为一次电流的下降电流)为5.658A。
选作控制器的IC拥有1.0V的典型电流自动切断电平,但容差值在0.9到1.1V之间。要确保所有单元都能提供要求的功率,需使用下限,并设定Rs值,以便让5.658A时它的电压为0.9V最小值的95%。这样便可实现5%的瞬态安全余量,并将Rs设定在0.15Ω。当然,会有5W左右的功率损耗,其最有可能由一个电流变压器产生。使用一个100:1的变压器时,Rs可能会增加至15Ω。后面内容,我们假设使用这样一个变压器。
图 3 二次电流加有效下降电流

实际上,下降电流(Ids)既没有流过电流变压器,也没有流过电源变压器,但却需要考虑其影响,它会影响电阻器Rs的电压。因此,需在电阻器Rs和IC的电流检测引脚之间增加一个电阻器Rdspri。在IC的电流检测引脚处,电流斜波被注入到电路中。这种电流斜波的存在,让IC电流检测引脚和电阻器Rs之间电阻器Rdspri中形成的等变电压(ramp voltage),等于Ids转变为一次电流在电阻器Rs中形成的电压。我们假设,一个等效下降电流正流经电阻器Rs,从而同时考虑到电源变压器和电流变压器绕组比。这种情况下,为了计算简单,我们将电阻器Rdspri设定为1kΩ,其远大于电阻器Rs。
接下来,计算Rdspri要求的dv/dt:

由该结果,我们可以计算得到1kΩ电阻器需要的电流斜波:

最大“开”时间的这种电流带来70.7 µA的峰值电流。
使用一个可编程、最大占空比 PWM 控制器(例如:UCC2807)时,通过将两个计时电阻器设定为相同值来将最大占空比设定为67%相对更加简单,如产品说明书所示。另外,这种组件的规格额定,计时电容器的谷值电压和峰值电压分别等于1/3VCC 和 2/3VCC。这样便得到一个 1/3VCC 的电压斜波幅值。知道这一点以后,我们现在便可以对电路进行设计,让它产生一个可注入到电流检测电路中的斜波电流,以向电流信号提供下降电流。
图 4 显示了用于产生期望电流的一个电路。该电路基于 UCC2807-1 控制 IC,VDD 设定为 11V。“三角”斜波的谷值电压和峰值电压为 3.667V 最小值和 7.33V 最大值,并且最小值到最大值的时间等于最大“开”时间。在该电路中,R3 等于 2 倍 R4。这样便让 Q6 基极的电压等于 1/3VCC,其为“三角”电压的谷值。由于“三角”引脚的电压在谷值到峰值(2/3VCC)之间摆动,R2 的电压便在 0 到 1/3VCC 之间线性变化。给 R2 选择一个值,让其获得 70.7 µA 的电流和 3.667 V 的 (51.8 kΩ) 电压,然后使用 Q5/R1 和 Q7/R6 构建起统一电流反射镜。这样,设计人员便可以生成电流检测信号,将所需电流加至电流检测信号,并拥有正确的形态和 1Kω 电阻计时。
图 4 用于生成预期 Rdspri 电流的电路

结论
三开关正向转换器在能量回收方面拥有许多独到之处,它可以将磁能和一次侧漏能量返回至源,无需使用缓冲器,降低了普通正向转换器中常见的电磁干扰。相比占空比大于50%的双开关正向拓扑结构,它同样具有许多优势。本文为您介绍了一个计算举例。在确定电流检测电阻器值,以及了解降压转换器50%以上占空比稳定工作所需下降电流的影响时,这种计算都是必需的。文章还介绍了增加转换器下降电流的一种方法。
 电子发烧友App
电子发烧友App






















评论