通过一个小型放大器和四个无源元件实现200 mW负载

概述

       在很多应用中，都需要用到能够为负载提供适当功率的放大器；另外还需保持良好的直流精度，而负载的大小决定了目标电路的类型。精密运算放大器能驱动功率要求不足50 mW的负载，而搭配了精密运算放大器输入级和分立功率晶体管输出级的复合放大器可以用来驱动功率要求为数W的负载。 但是，在中等功率范围内却没有优秀的解决方案。 在这个范围内，不是运算放大器无法驱动负载，就是电路过于庞杂而昂贵。

最近在设计惠斯登电桥驱动器时，这种两难处境更为明显。激励电压直接影响失调和范围，因此需要具有直流精度。这种情况下，源极电压和电桥之间的容差不足1 mV。 若以7 V至15 V电源供电，则电路必须以单位增益将电桥从100 mV驱动至5 V。

使问题变得更为复杂的是，它能使用各种不同的桥式电阻 例如，应变计的标准阻抗为120 Ω或350 Ω。若采用120 Ω电桥，则放大器必须提供42 mA电流，才能保持5 V电桥驱动能力。 此外，电路驱动能力必须高达10 nF。 这是考虑电缆和电桥耦合电容后得到的数值。

放大器选择

设计该电路的第一步，是选择可以驱动负载的放大器。 其压差（VOH） 在目标负载电流情况下，必须位于电路的可用裕量范围内。 针对该设计的最小电源电压为7 V，最大输出为5 V。若裕量为250 mV，则可用裕量（VDD – VOUT）等于1.75 V。目标负载电流为42 mA。

精密、双通道运算放大器 ADA4661-2 具有轨到轨输入和输出特性。 该器件的大输出级可驱动大量电流。 源电流为40 mA时，数据手册中的压差电压规格为900 mV，因此可轻松满足1.75 V裕量要求。

压差限制了电路采用低压电源工作，而功耗则限制了电路采用高压电源工作。 可计算芯片升温，确定最大安全工作温度。 MSOP封装简化了原型制作，但LFCSP封装的热性能更佳，因此如有可能应当采用LFCSP封装。 MSOP的热阻（θJA） 等于142°C/W，LFCSP的热阻等于83.5°C/W。 最大芯片升温可通过将热阻乘以最大功耗计算得到。 当电源为15 V且输出为5 V时，裕量为10 V。最大电流为42 mA，因此功耗为420 mW。 最终的芯片升温（MSOP为60°C，LFCSP为35°C）限制最大环境温度为65°C （MSOP）以及90°C （LFCSP）。

为保持精确的电桥激励电压，芯片和封装的组合热性能同样十分重要。 不幸的是，驱动大输出电流时，某些运算放大器的性能下降明显。 输出级功耗使得芯片上的温度梯度极大，从而导致匹配晶体管和调节电路之间的不平衡。 ADA4661-2设计用于驱动大功率，同时抑制这些温度梯度。

反馈环路稳定

满足负载-电容规格不容易，因为大部分运算放大器在不使用外部补偿的情况下无法驱动10 nF的容性负载。 驱动大容性负载的一种经典技巧，是使用多个反馈拓扑，如图1所示。图中隔离电阻RISO将放大器输出和负载电容CLOAD隔离。 将输出信号 VOUT 通过反馈电阻 RF进行回送，便能保持直流精度。 通过电容 CF反馈放大器输出，可保持环路稳定性。

如需使该电路有效，RISO 必须足够大，以便总负载阻抗在放大器的单位增益频率下表现出纯阻性。 这是很困难的，因为该电阻上会有电压下降。 通过分配最差情况下的剩余电压裕量，可确定RISO 的最大值。 6.75 V电源以及5 V输出允许1.75 V总压差。 放大器 VOH 占用总压差的900 mV，因此电阻上的压降最高允许达到850 mV。 如此，便可将RISO 的最大值限制为20 Ω。2 nF负载电容在该放大器的单位增益交越频率4 MHz处产生一个极点。 显然，多反馈无法满足该要求。

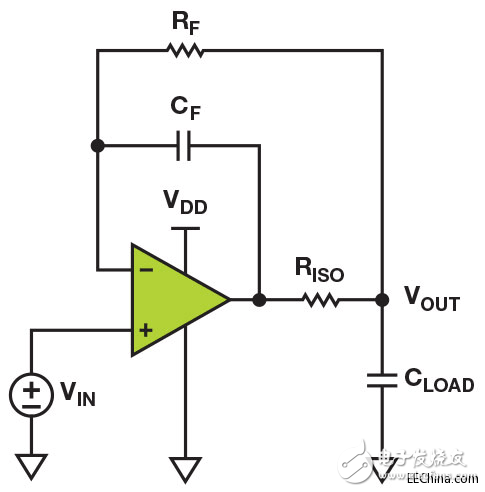
图1. 多反馈拓扑

另一种稳定重载缓冲器的方法是使用混合单位跟随器拓扑，如图2所示。这种方法通过降低反馈系数，强迫反馈环路在较低频率处发生交越，而非尝试移除负载-电容形成的极点。 由于存在负载极点，因此会产生过多相移；通过强迫环路在发生过多相移之前完成交越，便可实现电路稳定性。

T反馈系数是噪声增益的倒数，因此人们可能得出结论，认为这种方法摈弃了采用单位增益信号的原则。 若电路采用传统反相或同相配置，那么这种观点是正确的。但若对原理图作深入考察，便会发现两个输入均被驱动。 分析该电路的一种简便方法是将 –RF/RS 反相增益与 （1 + RF/RS）同相增益相叠加。 这样便可得到以+1信号增益以及 （RS + RF）/RS噪声增益工作的电路。 针对反馈系数和信号增益的独立控制允许该电路稳定任何大小的负载，但代价是电路带宽。

然而，混合单位跟随器电路具有某些缺点。 第一个问题是，噪声增益在所有频率下都很高，因此直流误差（如失调电压，VOS） 通过噪声增益而放大。 这使得满足直流规格的任务变得尤为艰难。 第二个缺点需对放大器的内部工作原理有一定了解。 该放大器具有三级架构，采用级联式米勒补偿。 输出级有自己的固定内部反馈。 这使得外部反馈环路有可能实现稳定，同时使输出级反馈环路变得不稳定。

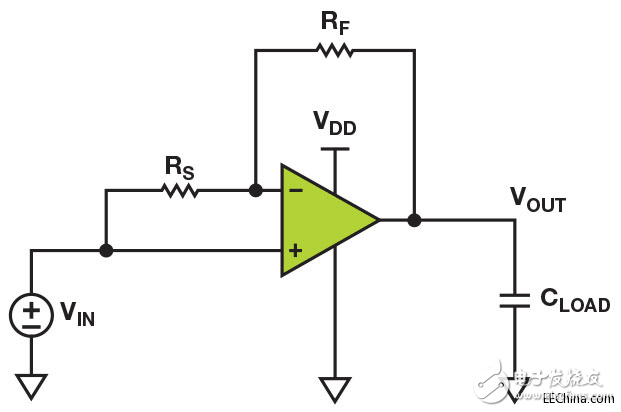
图2. 混合单位跟随器拓扑

通过将两个电路的工作原理相结合，便可解决这两个缺点，如图3所示。多反馈分隔低频和高频反馈路径，并加入了足够多的容性负载隔离，从而最大程度减少输出级的稳定性问题。 利用电桥电压，通过反馈电阻RF驱动低频反馈。 利用放大器输出，通过反馈电容 CF驱动高频反馈。

在高频时，电路还表现为混合单位跟随器。 高频噪声增益由电容阻抗确定，数值等于（CS + CF）/CF。该噪声增益允许反馈环路在一个足够低的频率上完成交越，而负载电容不会降低该频率处的稳定性。 由于低频噪声增益为单位增益，因此可保持电路的直流精度。

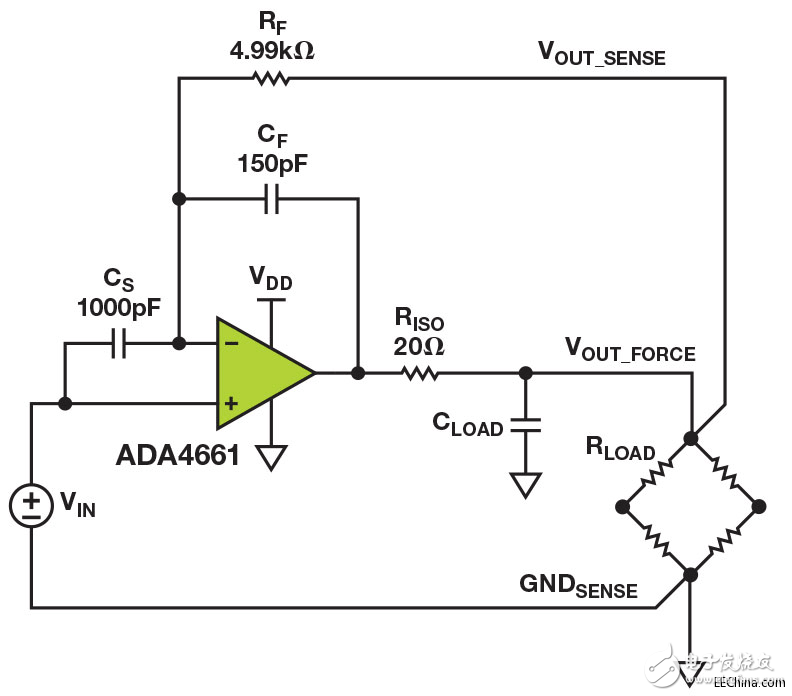
图3. 电桥驱动器原理图

保持直流精度要求十分留意信号走线，因为电路中存在大电流。 从42 mA的最大负载电流中，仅需7 mΩ 即可产生300 µV压降；该误差已相当于放大器的失调电压。

解决这个问题的一种典型方法是使用 4线开尔文连接，利用两个载流连接（通常称为“强制”）驱动负载电流，另外两线为电压测量连接（通常称为“检测”）。 检测连接必须尽可能靠近负载，以防任何负载电流流过。

对于桥式驱动器电路而言，检测连接应在电桥的顶部和底部直接实现。 在负载和检测线路之间不应共享任何PCB走线或线缆。 GNDSENSE 连接应当经路由后回到电压源VIN。 例如，假设激励为DAC，则GNDSENSE 应当连接DAC的REFGND。 电桥的GNDFORCE 连接应当具有专用的走线并一路连接回到电源，因为允许桥式电流流过接地层将产生不必要的压降。

误差预算

该电路的直流误差预算如表1所示，主要由放大器的失调电压和失调电压漂移所决定。 它假定工作条件处于最差情况范围内。 总误差满足1 mV要求，并大幅优于该要求。

表1. 误差预算

参数条件计算误差

失调电压0 V 《 VCM 《 5 V　300 µV

6.75 V 《 VDD 《 15 V

失调电压漂移0 V 《 VCM 《 5 V300 µV/°C × 110°C341 µV

6.75 V 《 VDD 《 15 V

–40°C 《 T 《 +70°C

功耗VDD = 15 V等式1168 µV

0 V 《 VCM 《 5 V

增益误差0 V 《 VCM 《 5 V5 V × 1/（105 dB + 1）27 µV

–40°C 《 T 《 +125°C

电源抑制6.75 V 《 VDD 《 15 V8.25 V/120 dB8 µV

总误差844 µV

表中的第三项表示功耗误差。 放大器功耗会增加芯片温度，因此与环境温度下的无负载电流情况相比，失调电压产生漂移。 最差情况下的误差计算采用最高电源电压、最高输出电压以及最低阻性负载，如等式1所示。注意，放大器上的最差情况压降通过 RISO 电阻得以部分降低。

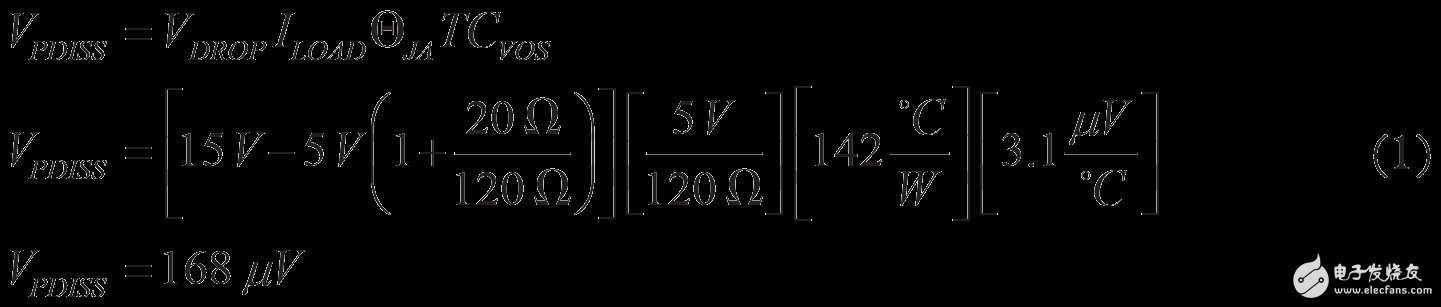
直流测量结果

误差电压等于输入电压VIN， 和负载电压VOUT之差。 图4显示原型电路的误差电压与负载电压的关系。 桥式驱动器电路中的最大误差源是失调电压和失调电压漂移。 由于放大器功耗而产生的额外误差与桥式电压有关。 电源电压对功耗的影响可从不同颜色的曲线中看出来。 黑色曲线功耗最低（50 mW），电源电压最小（7 V）。 芯片仅升温7°C，因而该曲线代表室温失调电压与该器件共模电压的关系。

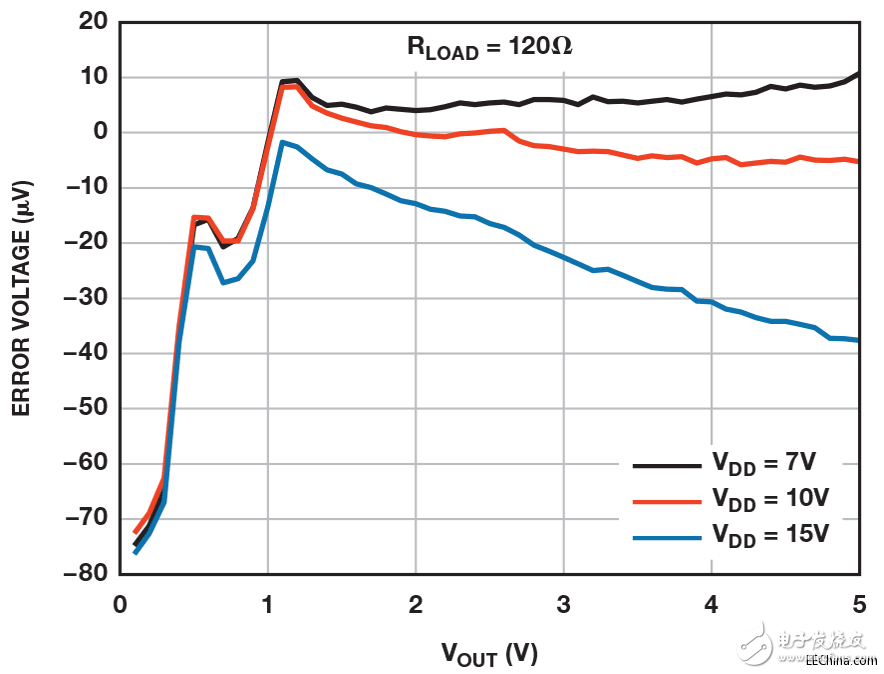
图4. 误差电压与输出电压的关系

色（10 V）和蓝色（15 V）曲线分别代表175 mW最大功耗和385 mW最大功耗下的性能。 随着输出电压的上升，额外的功耗使芯片升温25°C至55°C，导致失调电压发生漂移。 该额外热误差曲线形状为抛物线形，因为当VOUT 为VDD一半时，具有最大功耗。

电源在很大程度上依赖失调电压，这表示应当考虑该电路的电源抑制。 图5显示扫描电源电压并固定输出电压时的误差电压。 黑色曲线表示轻载情况，此时放大器电源抑制（PSR）起主要作用。 就该器件而言，10 µV变化表示118 dB PSR。 红色和蓝色曲线显示输出消耗额外功耗（由于负载为350 Ω和120 Ω典型桥式电阻）的结果。红色和蓝色曲线的有效PSR分别为110 dB和103 dB。

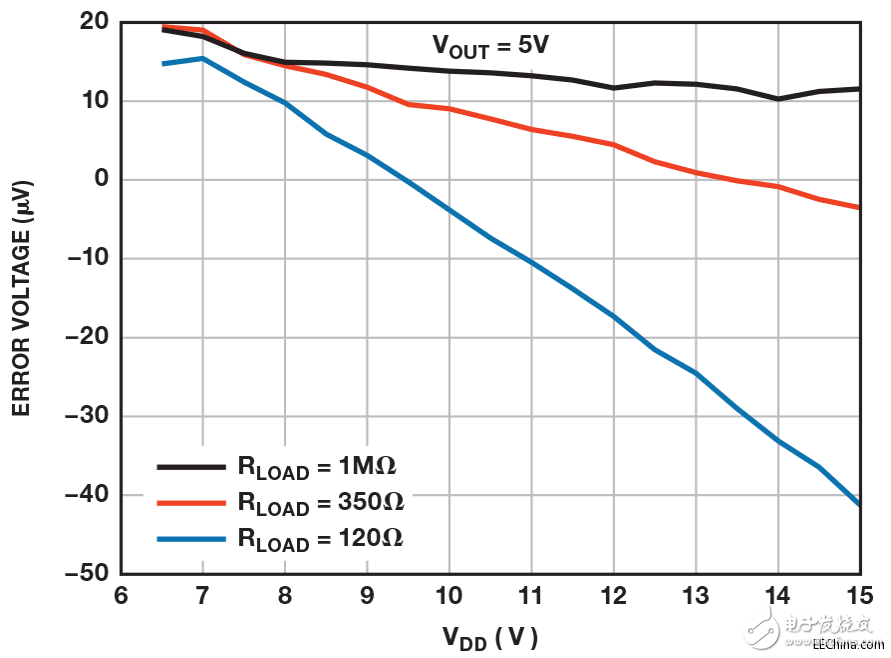
图5. 误差电压与电源电压的关系

该电路性能显然取决于失调漂移与温度的关系。目前为止，在所有与温度有关的误差计算中均采用了TCVOS 规格。 需要为该假设找到合理的解释，因为芯片温度由于放大器功耗与环境温度的改变有所不同而上升。 前者在芯片表面形成较大的温度梯度，影响放大器的微妙平衡。 这些梯度会使失调电压漂移相比数据手册规格而言要差得多。 ADA4661-2经特殊设计，其功耗极大且不影响失调漂移性能。

图6显示失调漂移测量值与温度的关系。额定性能重现于黑色曲线，并具有低电源电压与高阻性负载（–1.2 µV/°C）。 红色曲线显示120 Ω桥式负载结果。 值得注意的是，曲线的形状未发生改变；它仅仅由于芯片升温（6.4°C）而向左平移。 蓝色曲线显示电源电压上升至15 V时的结果——此时可测量电路的最大功耗。 同样地，曲线形状不发生改变，但由于芯片升温55°C而向左平移。 内部功耗已知（385 mW），因此可计算系统的实际热阻 （θJA） ，即143°C/W。 重要的是需考虑工作的环境温度范围。 最大芯片温度不应超过125°C；这意味着对于最差情况负载而言，最大环境温度为70°C。

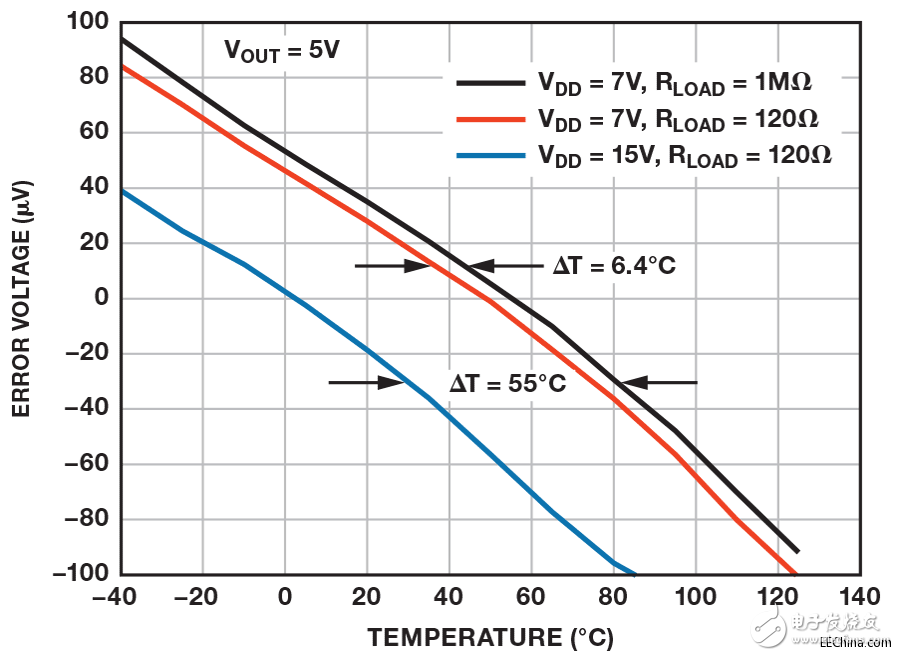
图6. 误差电压与环境温度的关系

瞬态测量结果

电路的阶跃响应是评估环路稳定性的简便方法。 图7显示高电阻电桥在容性负载范围内的阶跃响应测量值；图8显示低电阻电桥在同样条件下的测量值。 由于反馈网络的极点-零点二联效应 ，该电路的阶跃响应具有过冲特性。 该二联响应存在于基波中，因为电路反馈系数从低频时的单位增益下降至高频时的0.13。 由于零点相较极点而言处于更高的频率，阶跃响应将始终过冲，哪怕相位裕量远大于适当值。 此外，二联效应在电路中具有最大的时间常数，因此趋向于对建立时间产生主要影响。 当采用高阻性负载以及1 nF容性负载时，电路具有最差情况下的稳定性以及输出级振铃。

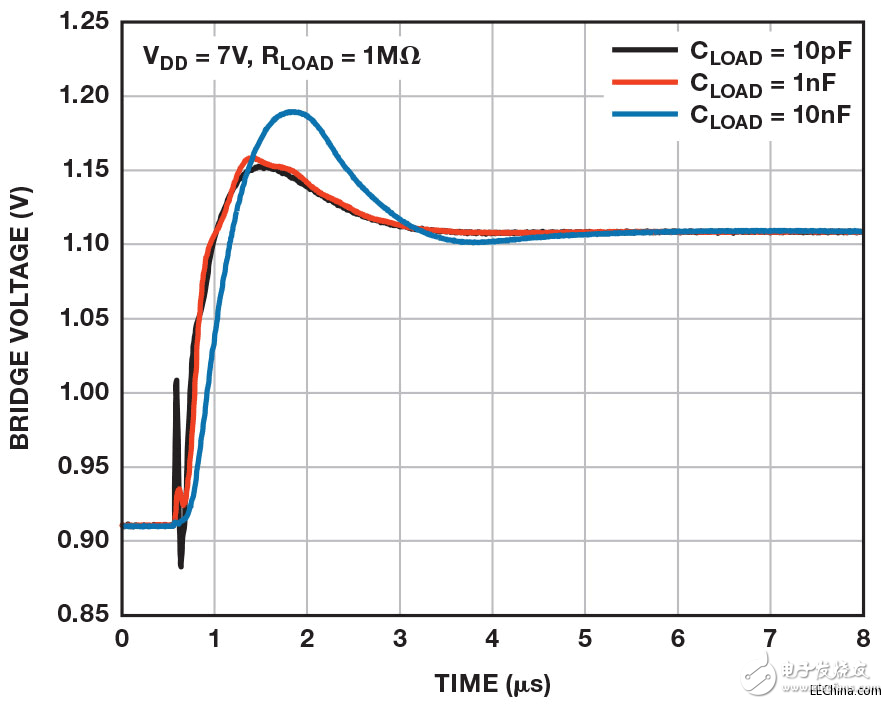
图7. 无负载阶跃响应

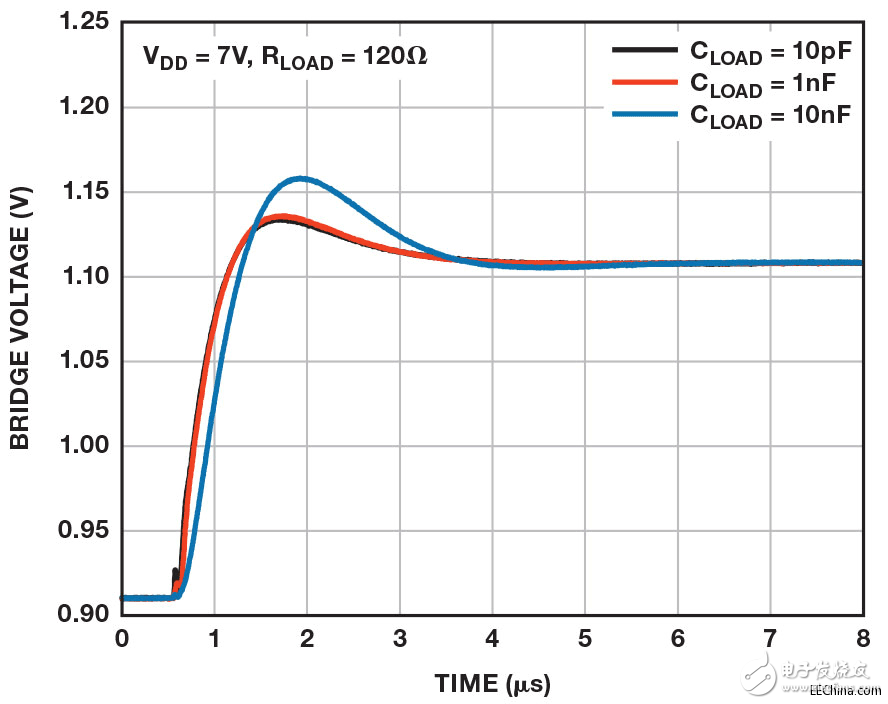
图8. 有负载阶跃响应

结论

本文所示之负载驱动器电路可为低至120 Ω的阻性负载施加5 V电压，而总误差不超过1 mV，并且能稳定驱动高达10 nF总电容。 电路符合其额定性能，并能以7 V至15 V的宽范围电源供电，功耗接近400 mW。 通过以±7 V电源为放大器供电，该基本电路便可扩展驱动正负载和负负载。 全部性能通过一个3 mm × 3 mm小型放大器以及四个无源元件即可实现。