本文将尝试用非数学方法解释∑-Δ转换器,并涵盖噪声整形和过采样等基本概念,并结合一些示例来进行说明。这些概念与数字抽取滤波器随后结合在一起,以揭开∑-Δ转换器的神秘面纱。本文还包括一阶和二阶∑-Δ模数转换器的基本知识以及∑-Δ调制器的阶数如何影响模数转换器的性能。
引言
目前,有许多应用经常要求模数转换器具有高分辨率,而不是高精度,从而出现了对∑-Δ模数转换器的需求。为了了解∑-Δ转换器,人们必须深入了解频域中所涉及的复杂数学计算来钻研控制环路理论。但本文将让您了解一些非常重要的概念,如噪声整形、过采样和∑-Δ调制器背后使其区别于其它转换器架构的所有魔幻性能,尽可能避免数学复杂性,使您能够可视化感受事物的移动。
要了解∑-Δ模数转换器,首先需要了解噪声整形和过采样等基本概念。噪声整形可通过两种模拟来阐释。
什么是“噪声整形”?通用示例如下
比如说,某个商品的价格是9.9卢比,您购买该商品已有10天。下图是店主让您支付此商品的价格图。
不管是0.1或0.5,每天都会产生一些误差,但在10天结束后,商品的价格最终确实为9.9卢比。这种平均误差被称为噪声整形。
但是只有店主每天都跟踪误差,才会发生这种情况。因此为了跟踪误差,系统应有一个存储器。
表1:商品的每日价格
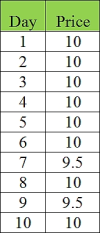
Day: 天数;Price: 价格
通过数模转换器解释的噪声整形
如果我们的普通数模转换器包括噪声整形,将会怎样?我们允许数模转换器整形噪声。我们让它不只给出一个数字,而是两个或三个数字,使平均值接近理想状态。
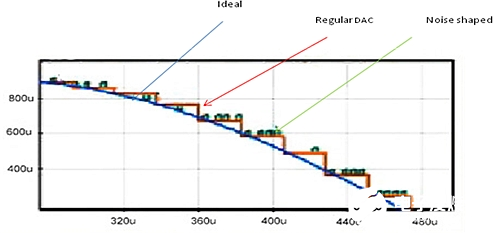
图 1:时域中普通数模转换器与噪声整形数模转换器的比较(Ideal: 理想状态;Regular DAC: 普通数模转换器;Noise shaped: 噪声整形)
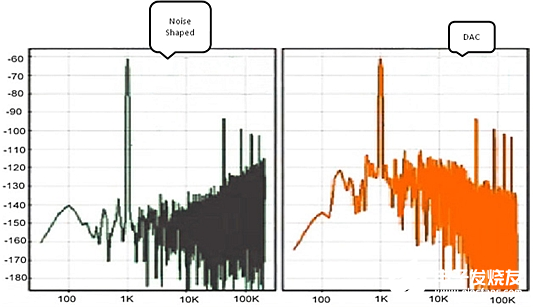
图 2:频域中噪声整形与普通数模转换器的比较(Noise Shaped: 噪声整形;DAC: 数模转换器)
如图1所示,如果我们真地遵循绿色模式,我们就会将数值上下移动一点。看起来似乎很糟糕,因为我们已经为此数模转换器增加了噪声。它甚至没有使数值保持稳定。我们没有引入任何新级别,它们早已存在于普通的数模转换器中。
现在,看看图2中两个系统的傅立叶分析。令人惊喜的是,我们原以为会有损性能的绿色的东西,实际上却使数模转换器运行地更好。与普通数模转换器相比,噪声整形数模转换器中噪声低于1KHz的区域更小,因而能够更好地代表1KHz信号。
过采样概述
无论何时通过频率Fs对信号采样时,都假设误差过程的随机变量与量化噪声相关(与信号不相关);误差是一个白噪声过程,而且量化噪声功率(q/√12,其中q 为1 LSB)统一最大为Fs/2。
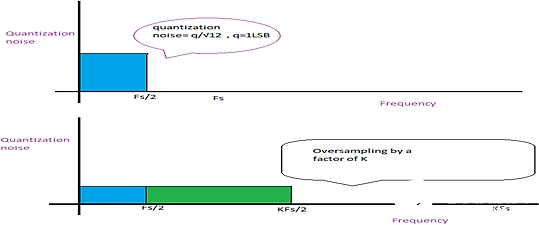
图 3:过采样效应(Quantization noise: 量化噪声;Frequency: 频率;Oversampling by a factor of K: 按K因子的过采样)
当按K因子进行过采样时,相同的量化噪声功率均匀地分布,最高达KFs/2,因此量化噪声功率在Fs/2区域中会降低。
∑-Δ转换器的魔幻性能
从下面曲线中您可以确定什么?
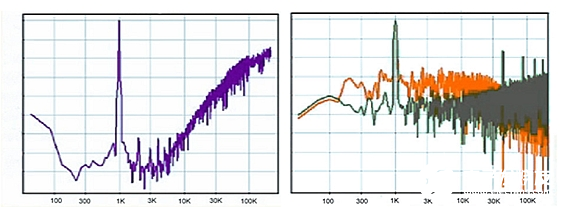
图 4:∑-Δ(左侧)与频域中普通/噪声整形数模转换器(右侧)的比较
在图4中,左侧远远超过右侧中两种噪声水平中的任何一个。只要此系统在左侧,它所表示的1 KHz信号都会比右侧其它两个的信号要好。
此系统是什么?
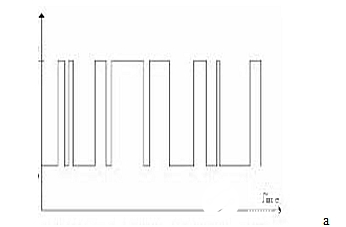
图 5:∑-Δ调制器的时域信号(a)和普通近似正弦波(b)
这里甚至不是数模转换器!它只是一个系统,提供在+/-全范围的信号,但在与它关联的信号频率附近,底噪仍会更低。我们如何把握它?
图5b是普通数模转换器的输出,我们至少可以视其为正弦波。但图5a呢?它如何才能更好地代表1KHz信号呢?
这里就是此∑-Δ转换器的魔幻性能。
增量调制基础知识中就包含了答案。那么增量调制是什么?
增量调制(DM或Δ-调制)是模数或数模信号转换技术,用于传输对质量要求不高的语音信息。DM是差分脉冲编码调制 (DPCM)最简单的形式,其中连续样本之间的差异被编码成n比特数据流。在DM中,将所传输的数据减少到1比特数据流。
它采用预测算法运行。以简单情况为例,它预计当前的采样与之前的采样相同。 然后比较这两次采样,如果输入较大,则发送a +Δ,如果输入较小,则发送a –Δ;在接收器端也类似,保持跟踪+/- Δ,这样系统能够很好地辨别信号值何时增加、何时降低,从而可重建信号。虽然有两个相关问题,即斜率过载和粒度,但我们不会深入钻研,从而能够更多地关注发送误差值而非实际值这一个重要方面,如果是正弦波,仍会重组输入信号。
以店主为例,如果他第一天收取9卢比,第二天收取9.5卢比,第三天收取8卢比,而第四天则收取11卢比,但是即使这样安排,10天后,您仍会为此商品支付9.9卢比,从而把您搞糊涂。随机误差只将噪声转换到更高频率,在目标带宽中产生良好的信噪比。
∑-Δ模数转换器:噪声整形 + 过采样
我们已经了解了噪声整形和过采样的基本概念。现在让我们了解∑-Δ调制器如何利用这些概念,提供比其他转换器更好的动态性能(高信噪比)。
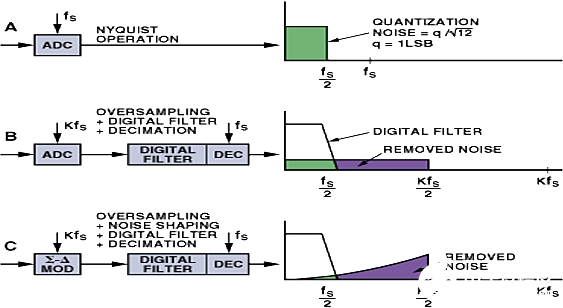
图 6:过采样和噪声整形(NYQUIST OPERATION: NYQUIST定理运算;QUANTIZATION NOISE: 量化噪声;OVERSAMPLING: 过采样;DIGITAL FILTER: 数字滤波器;DECIMATION: 抽取;REMOVED NOISE: 移除的噪声;NOISE SHAPING: 噪声整形)
图A:量化噪声均匀分布,最高达Fs/2
图B:让我们按K因子进行过采样,这会产生什么影响?相同的噪声分布,最高达KFs/2,导致噪声较低,最高达Fs/2。
图C:在此,我们所涉及的噪声整形会将噪声转换到更高频率,从而进一步降低相关频段内的噪声。
因此∑-Δ转换器采用上图6所示的噪声整形和过采样技术,从根本上降低了目标带宽中的噪声。
数字抽取滤波器
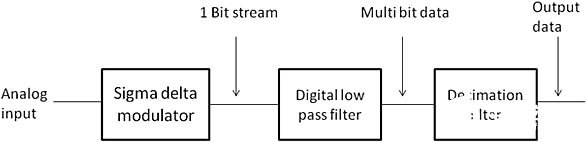
图 7:数字抽取滤波器(1 Bit stream:1比特流;Multi bit data: 多比特数据;Output data: 输出数据;Analog input: 模拟输入;Sigma delta modulator:∑-Δ调制器;Digital low pass filter: 数字低通滤波器;Decimation filter: 抽取滤波器)
∑-Δ调制器的单比特流输出到数字抽取滤波器,平均值降低,然后降低采样数,从而以目标采样率Fs生成N位采样。数字滤波器是求平均值的低通滤波器。它衰减量化噪声,并删除目标频段的别名。一般来说,Sinc传输函数可用作低通滤波器。
对输入信号进行过采样,以便降低量化噪声,因此可在引入失真的情况下消除冗余数据。抽取过程仅降低了输出采样率,同时保留必要的信息。带Sinc传输函数的FIR滤波器可通过抽取进行数字滤波。
一阶和二阶∑-Δ模数转换器
首先,让我们来看看一阶∑-Δ模数转换器的基本功能。
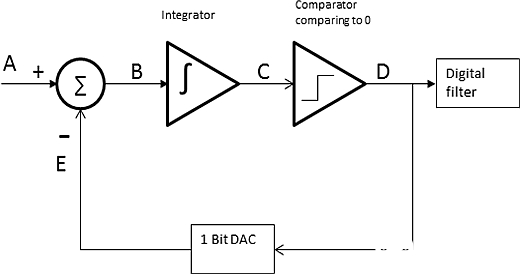
图 8:一阶∑-Δ模数转换器(Integrator: 积分器;Comparator comparing to 0: 比较器(与0进行比较);Digital filter: 数字滤波器;1 Bit DAC: 1位数模转换器)
在图9中,A表示固定输入3VDC。B、C、D和E为信号路径中的各点。数模转换器的基准电压为8V。
最初,B、C、D和E都为0。在每步中,积分器累积输入信号和反馈信号之间的误差,然后馈送到与0进行比较的比较器。在比较过程中,比较器在每步中都引入量化噪声。比较器的输出传输到将数字信号转换为模拟电压的1比特数模转换器。由于数模转换器的基准电压为8V,因此“1”表示8V,而“0”表示0V。数模转换器的输出再次与输入信号进行比较。
表2:一阶∑-Δ模数转换器

Less randomized error: 更少的随机误差
3 1‘s representation of 3V: 3个1表示3V
经过8个步骤之后,此模式重演。因此,我们可以看到,反馈机制强制反馈信号等于输入电压信号。在此环路中,积分器可作为噪声整形滤波器,而比较器/量化器可引入量化噪声。
从表3中我们可以看到,3个1在此表示3V信号。输入信号的值越高,1的数量就越多。
二阶∑-Δ模数转换器
二阶∑-Δ模数转换器与一阶的类似,只是增加了一个积分器。
让我们看看二阶∑-Δ调制器,了解一阶和二阶之间的基本区别。
从表3可以看出,二阶∑-Δ模数转换器的工作机制几乎与一阶的类似,但它有更多的随机误差。在这种情况下,6个1表示16个步骤中的3V,即每8个步骤中有3个1。
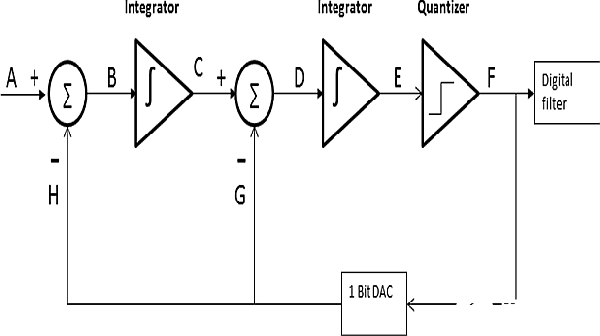
图 9:二阶∑-Δ模数转换器(Integrator: 积分器;Quantizer: 量化器;Digital filter: 数字滤波器;1 Bit DAC: 1比特数模转换器)
表3:二阶∑-Δ调制器
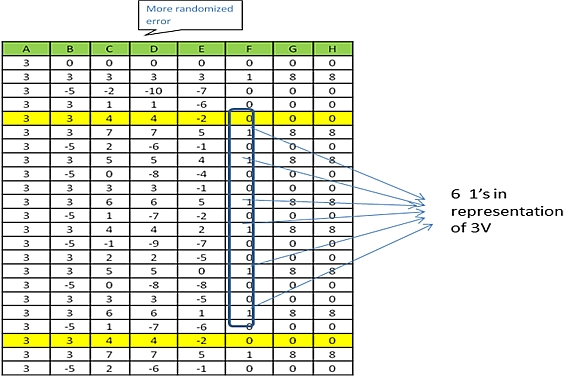
More randomized error: 更多的随机误差
6 1’s representation of 3V: 6个1表示3V
一阶和二阶有何差别?
从根本上说,由于随机误差更多,因此二阶系统将输出噪声转换为更高的频率,从而在目标带宽产生低噪声,但代价是需要更多硬件。
因此阶数越高,随机误差就越多,而目标带宽中噪声则越低,但所有这些都以增加硬件为代价。
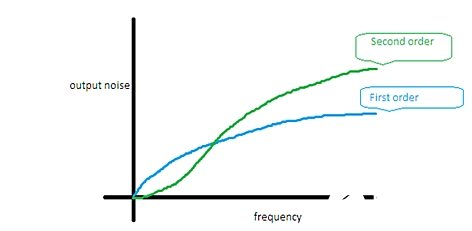
图 10:一阶和二阶∑-Δ模数转换器的输出噪声(Output noise: 输出噪声;Second order: 二阶;First order: 一阶;frequency: 频率)
小结
本文涵盖了∑-Δ模数转换器的基本原理。它特别专注于了解关键概念,如过采样、噪声整形、抽取等,不涉及数学问题,旨在更好地了解更高阶的∑-Δ模数转换器。
责任编辑:gt
 电子发烧友App
电子发烧友App




















评论