作者:ADI 公司 Mark Alexander、Derek F. Bowers
目前,电路仿真领域呈现采用全方位电路仿真方法的趋势。我们认为,在所有安装的电路仿真器中,有75%用于系统设计,而不是IC设计。几乎所有这些仿真器都是SPICE的变体。随着电子行业不断发展,系统工程师面对日益增多的集成电路,尤其是无处不在的运算放大器,也需要愈加精准的模型。但是,这些IC器件的速度和复杂性不断提高,给初期的SPICE开发人员带来了始料未及的问题。
由于典型的运算放大器中包含大量有源器件,仅使用晶体管级模型的电路仿真会消耗大量时间,特别是电路中包含多个运算放大器时。由于涉及多个非线性方程,即使是简单的半导体器件模型也会消耗大量计算时间。在某些情况下,完成整个仿真所需的时间可能超过构建工程原型所需的时间。显然,这种情况完全背离了使用SPICE的初衷。
幸运的是,我们可以通过使用尽可能准确地表示运算放大器的宏模型来缩短仿真时间,而无需使用大量晶体管或其他非线性器件。然而,无论出于何种意图和目的,要设计一个能完全模拟实际器件的宏模型是一个相当大的挑战。对于电路设计人员来说,运算放大器模型要切实起到作用,则不能只涵盖所有重要的DC参数,还要能够在远超单位增益交越频率的区域内合理地仿真近似AC特性。
现有的宏模型是不够的
许多运算放大器的宏模型已包含在多个可用软件仿真器的器件库中。这些模型大多数都是基于Graeme Boyle和他的同事(见参考文献1)所做的初期工作,他们在20世纪70年代中期开发了一些宏模型,以缓解当时已经超负荷的大型计算机的CPU时间紧张问题。Boyle几乎去除了宏模型中的所有晶体管,只保留了两个晶体管。保留的这两个器件构成了运算放大器的差分输入级;后续的所有级都采用线性控制源、无源元件和二极管来实现。输入级中保留的晶体管有助于仿真实际影响,例如偏置电流,以及输出dV/dt随差分输入电压的变化。
Boyle方法大大减少了所有非线性元件的数量,所以每个放大器所需的仿真时间也大幅缩短。相比完全采用晶体管的仿真,Boyle结构确实有明显改善,但该结构仍有一些不足之处,这也促进了新的宏模型的开发。该结构具有以下缺陷:
-Boyle模型只提供两个极(没有零)来显示整个放大器的频率响应——这种配置仅适用于较慢的运算放大器,完全不适合如今速度更快的器件。
-所有内部产生的节点电压都以地为基准,即使放大器相对于地“浮空”。这种配置不能体现运算放大器的真实运行状况——几乎所有可用的器件都不提供接地参考。
-输出端电流从连接到地的受控源流出,而不是像在实际放大器中那样从电源轨流出。此特性完全排除了基于放大器的输出电流(在电源轨之间正确分流)来仿真电路的情况。
理想元件可以降低复杂性
开发原始的Boyle模型(图1)的电路拓扑结构时,使用了两种基本的宏模型建模方法(称为简化法和构造法),这两种方法在开发新宏模型时也非常有用。
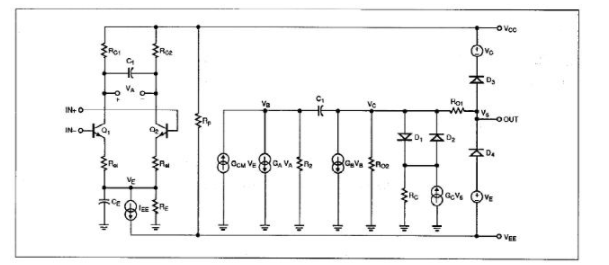
图1:Boyle运算放大器宏模型的一个重大缺陷是所有电压都以地为基准
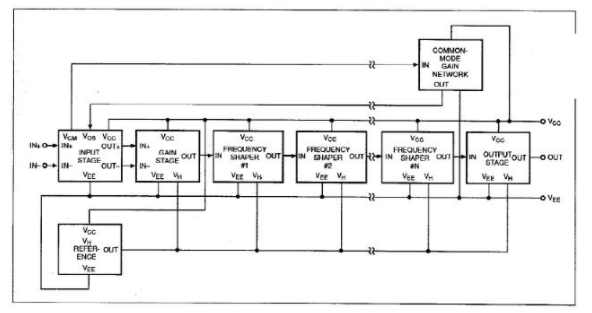
图2:新运算放大器宏模型本质上是模块化的。在运算放大器设计中,可以通过级联任何构建模块来获得任意数量的极和零点。
这种简化技术使用简单的理想元件来代替电路的实际部分,从而持续降低运算放大器主要内部级的复杂性。因此,可以通过利用此方法的功能模块来高度仿真实际电路。在图1中,输入级模型就是一个很好的简化示例。该模型保留了发射极耦合对的差分输入特性,但消除了所有有源负载;它用理想元件代替尾电流源;并承担产生第二放大器极的任务。增加一个电容(CE)即可使该模型在此级中提供一个极,而减少元件总数则能加快仿真运行速度。
另一方面,可以使用构造法构建一个完全由理想元件组成的电路模块,高度仿真器件实际部分的行为。遗憾的是,构造法常常会导致一些子部分与实际等效部分毫不相似。图1的输出级就是一个很好的示例:它提供了必要的输出电压限幅,具有正确的输出电阻,还提供了短路限流值;但与实际运算放大器原理图没有一点相似之处。
开发改进的宏模型
开发新的宏模型(图2)的目的是创建一个能够像实际运算放大器一样运行的模型;但它仍然必须足够简单,可以作为一个通用模型使用。图3、图4和图5显示该模型由处理输入信号的几个级联部分组成。

图3:新模型的输入级与Boyle模型的输入级相似,但之后所有级的结构都截然不同
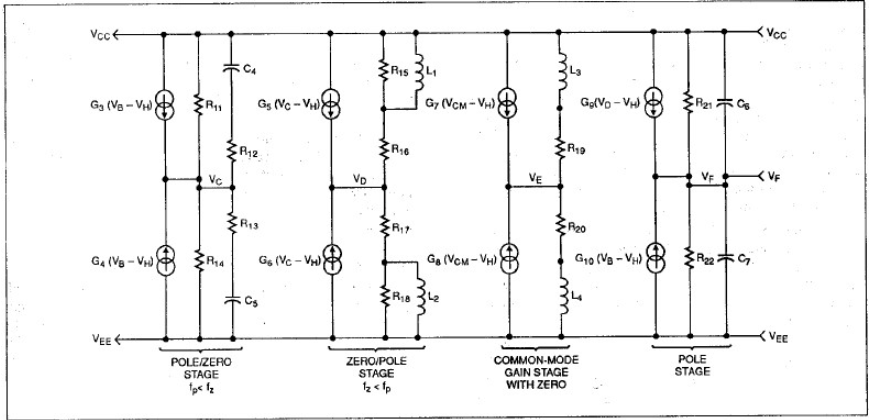
图4:除提供零点的共模增益级外,还提供三种类型的频率成形网络
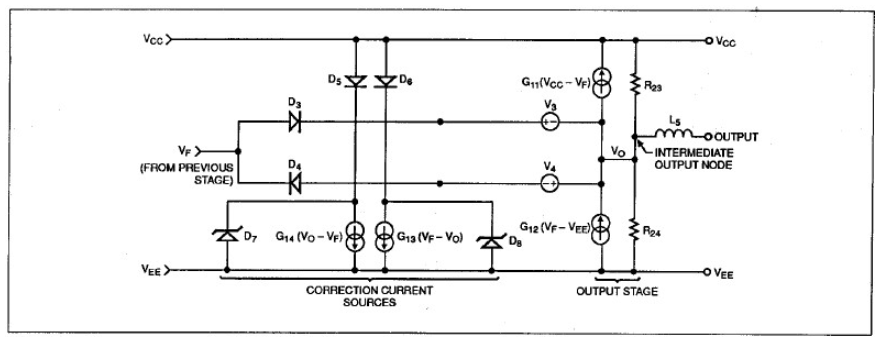
图5:新输出级还配有电流源,对供电轨之间的负载电流正确分流
由于该模型在构建时采用了简化技术,所以其输入级与Boyle模型非常相似。但是,由于生成新模型的剩余部分时采用了构造法,在输入级之后,这两个宏模型毫无任何相似之处。注意,在任何信号处理模块中都没有接地参考。相反,在实施差分至单端转换后,所有内部产生的节点电压都以供电轨之间的中点为基准。这个中点在模型中称为VH,由两个连接在供电轨之间的等值电阻产生。
在使用新宏模型对任何特定的运算放大器建模时,其最低要求基本上与Boyle拓扑的要求相同:一个差分输入级、一个增益级和一个输出级。这种配置可以产生基本的双极频率响应,且可以从仿真时间这个角度直接比较这两种宏模型。您可以在增益级和输出级之间添加单位增益极、极零点和零极点模块的任意组合,以获得所需的频率相关开环增益滚降。模块之间的区别在于:极零点模块产生的极点频率比零点低,而零极点产生的极点频率比零点高。
框图2“模型参数的计算”显示了基于图3、4和5所示的构建模块构建运算放大器所需完成的计算。只要给出所探讨的运算放大器的某些数据手册参数,结合必要的极零点位置,就可以使用计算器轻松完成这些计算。
图3中的输入级是一个简化双晶体管电路。新模型和旧模型的主要区别在于:在新模型中,输入级使用与实际运算放大器同类型的输入器件,即NPN或PNP双极性器件、P通道JFET(或者如果适用,使用N通道器件),或者MOSFET。Boyle模型只允许在输入级使用双极性器件,如果是对双极性输入运算放大器进行建模,这毫无问题。但是,如果使用Boyle技术对一个FET输入运算放大器建模,则必须大幅提高输入晶体管的电流增益,以获得所需的输入偏置电流。此外还必须通过发射极负反馈来降低其跨导。这些更改导致的结果是:无法在宽输入差分电压范围(一般是1至2V)内正确仿真FET输入放大器的输出dV/dt的常见变化。A降级之后的双极输入级具有线性化、双曲正切传递特性(见文献2),而FET输入级具有平方律传递特性(见文献3)。显然,这些特性并不对等。因此,由于FET输入级的参数计算并不比双极性级复杂,所以在模型中使用正确的输入器件是有意义的。
所有表现出非理想行为的输入级参数(如失调电压、失调电流和输入电容)都使用单独的理想元件进行建模。此外,在反相和同相输入端之间连接两个等值电阻,以产生共模输入电压。模型的后续部分会用到输入电压,先进行扩展和频率成形,之后反馈到输入级用于修正失调电压。
该模型假设输入晶体管是完全匹配的,且没有任何会改变整体频率响应的结电容。但是,通过为双极性级选择合适的电流增益,或为FET级选择合适的栅极漏电流,它也可以得出正确的输入偏置电流。通过使负载电阻值等于晶体管跨导的倒数,可以将差分对的电压增益设为单位增益。这个假设简化了确定压摆率限制元件的计算。为方便起见,将输入级的尾电流标称值设为1 mA;但是,这个值可以降低到100µA、10µA或1µA,具体取决于放大器的总静态电流。
增益级的特性
该模型的开环增益通常在一个单级(见图3)中实现,该级由两个电压控制电流源、两个电阻、两个电容和一个电压限制网络组成。在这个级中,也会发生差分至单端信号转换。电压限制网络由一对二极管组成,每个二极管都连接到自己的电压源。该网络防止增益级和模型的其他内部节点在输入过载驱动条件下出现超过电源轨电压的摆幅。在开环增益级必须限制电压;否则,后续节点可能会尝试仿真大信号(数百千伏)的产生。
两个电容(与电阻并联)决定放大器主极点和压摆率。目前,宏模型只能处理对称的正负压摆率,因为对称是最容易仿真的情况。但是,未来的增强宏模型可能允许仿真对称正负压摆率之间的一些变化。最后,该级在这两个电压控制电流源上各添加一个直流分量,构成放大器静态电源电流的主要部分。
对运算放大器频率响应的研究表明,在大多数情况下,精确仿真实际器件在高频率下的增益和相位变化需要两个以上的极点。此外,不同类型的运算放大器具有不同数量的极点和零点。为了让这些不同类型的电路都能轻松转换成兼容SPICE的子电路(而不必每次都从头开始),那么一个真正的通用模型必须是高度模块化的,并且具有任意数量(大量)的极点和零点。所以,最终架构使用了所有单个运算放大器模型都通用的一些基本构建模块。这些模块如图4所示。
所有频率成形模块在DC条件下具有单位增益,因为每个电压控制电流源(VCCS)的gm都等于从VCCS(电压控制电流源)的每个节点连接至电源轨的电阻的倒数。这种拓扑结构优势在于,在为一个特定放大器生成模型时,可以标注单独的极点或极零点对。因而可以查看它们各自对放大器的净频率响应的影响,这样极零点调整变得非常容易。因为所有频率成形模块在DC条件下都具有单位增益,所以这个过程不会改变模型的DC开环增益。
图4中的共模增益级由两个VCCS组成,它们驱动两个等值电阻,每个电阻与一个电感串联连接至其中一个电源轨。电感仿真大部分放大器随着输入频率增加而表现出的CMRR的典型衰减。输入共模电压(相对于Vh节点)控制电流源。每个控制电流源的gm都等于相关电阻值除以DC条件下放大器的CMRR的值的倒数。
所以,从输入共模网络到内部共模增益节点的增益等于放大器的CMRR的倒数。(“增益”一词用在这里并不恰当,因为共模增益的值要远小于单位增益)。
SPICE仿真器的发展
电路仿真器SPICE及其增强版本SPICE2最初是加州大学伯克利分校在上个世纪70年代开发出来的(见参考文献4)。最初是为了帮助设计工程师在晶体管级分析集成电路(所以这个首字母缩略词是表示:Simulation Program with integrated Circuit Emphasis,集成电路模拟的仿真程序)。相比在实验室由人力计算,SPICE支持使用计算机评估设计,其速度更快,也更彻底。SPICE迅速流行,很快传播到系统级设计社区,受到IC设计人员的青睐。
初版SPICE是一个公用程序,仅象征性收取少量费用;但是,许多软件供应商都意识到需要一个完全受支持、可以调整和不断改进的商用电路仿真器。这类程序的第一个基于大型机的版本包括Meta-Software的HSpice、NCSS分时软件的I-Spice和电子工程软件的precision。近来,大部分大型机版本经过调整可用于工作站,还有一些可用于IBM PC和兼容产品。
SPICE的首个PC版本是由MicroSim Corp推出的PSpice。之后陆续推出了其他版本,例如Intusoft推出的IS-Spice。其他公司,包括ADI公司(提供一种名为Saber的行为仿真软件包)已经选择脱离传统的SPICE格式,放弃使用“盒装”电路元件来构建模型。相反,Saber基于严格定义的用一种称为Mast的特定建模语言编写的方程来控制任何所需电路模型的行为。
电感器在共模增益上增加一个零点,这相当于在共模CMRR上增加一个极点。共模电压,在经过扩展和适当的频率成形之后,按照理论要求输送回输入级。这一步通过将输入级偏置电压源变成单位增益电压控制电压源来实现,其直流分量等于放大器的VOS。
图5中并未完全显示输出级的操作。在接收所有适当的频率成形之后,内部运算放大器输出信号显示为以输出级处理之前的最后一个节点的Vh为基准的电压。输出模块中的两个电压控制电流源驱动两个连接至供电轨的等值电阻,就像其他模块一样。但是,此时,两个电压控制电流源的gm的排列方式使它们能够作为有源电流发生器。所以,每个gm源产生的电流恰好足以通过并行电阻提供所需压降。
当输出端没有负载时,该模型不会从任一电源轨吸取电流。所以,它表现得比较像是理想的单位增益B类输出级,且无交越失真。因为两个电阻的值都等于开环输出电阻的两倍,所以输出级看起来就像是以Vh为基准的电压源,具有正确的DC输出电阻。仿真正确的输出电阻意味着DC开环增益会在放大器加载时适当降低。
模型参数计算
以下公式可用于构建改进的宏模型,以实现任何运算放大器仿真。它分别针对每个可用的构建模块进行计算,并讨论了一些电源考量因素。
输入级和增益级计算
a. 通用计算
参考图3来确定此处提到的元件和信号。首先,选择IEE,其值要略小于放大器的总静态电流。为方便起见,可以将IEE设置为1mA、100µA、10µA或1µA,

(两个二极管均适用)。
您可以将数据手册中的一些参数直接运用到模型中。这些参数包括:
EOS =输入失调电压(仅限直流分量);
IOS = 输入失调电流;CIN = 输入电容。
b. 双极性输入级计算
首先,必须评估以下公式,确定是否可以使用新宏模型对讨论的运算放大器进行建模:

其中VT = 0.02585V(27°C时)。
如果此方程成立,可以继续进行接下来的计算。如果不成立,则必须修改模型,使其与特定的运算放大器匹配。

其中βF为输入晶体管的正向电流增益,IBIAS为输入偏置电流。
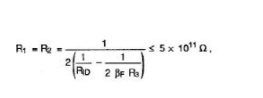
其中RID为差分输入电阻。如果RID不是指定的数据手册参数,则将R1和R2的值设为5 x 1011Ω。
c. JFET输入级计算
如果设计中包含JFET输入级,则使用栅极至源极截止电压VTO的默认值-2.000V。另外,将第一级电流源的名称改为ISS。主要计算是确定β,即JFET的增益系数:

其中RID为差分输入电阻(一般为1 x 1012Ω。
最后,可以将R5和R6的值设置为零,因为JFET输入放大器通常不需要降级。
频率成形级计算
要确认频率成形级的参数,请参见图4。在所有三类频率成形级中,为方便起见,将G3和G4设置为A/V的1 x 10-6倍。此外,fZ为零点频率,fp为极点频率。
然后,在极零点级,

其中,fCM为共模极。
输出级计算
要确认输出级的参数,请参见图5。二极管D7和D8的击穿电压标称值设置为50V。通过实验确定了电感L5的值。ROUT为开环输出阻抗;VT为0.02585V(27°C时);所有二极管的IS均为1 x 10-12A。所以:

其中,N为该模型中频率成形和共模增益级的总数;R一般为1 x 106Ω;此值以及频率成形级中G源的跨导,可以根据低功耗运算放大器适当调整;
IDC是增加至G1和G2源的直流偏移,以补偿模型的剩余部分消耗的电流和 的静态电流之间的差值
但是,这种简单的推挽式输出级存在一个微妙的问题。无论这个级是吸电流还是源电流,负载电流总是均匀分布在两个电源轨上,而实际输出级不会如此。所以,以源负载电流为例,净正电源电流的增加幅度只有流入负载中电流的一半。而负电源电流则是减少相同的量。为了补偿这种异常,会强制电流从正电源轨流向负电源轨,数量正好是负载电流的一半。这种校正电流必须始终沿着相同的方向流动——即使输出电流的极性相反。
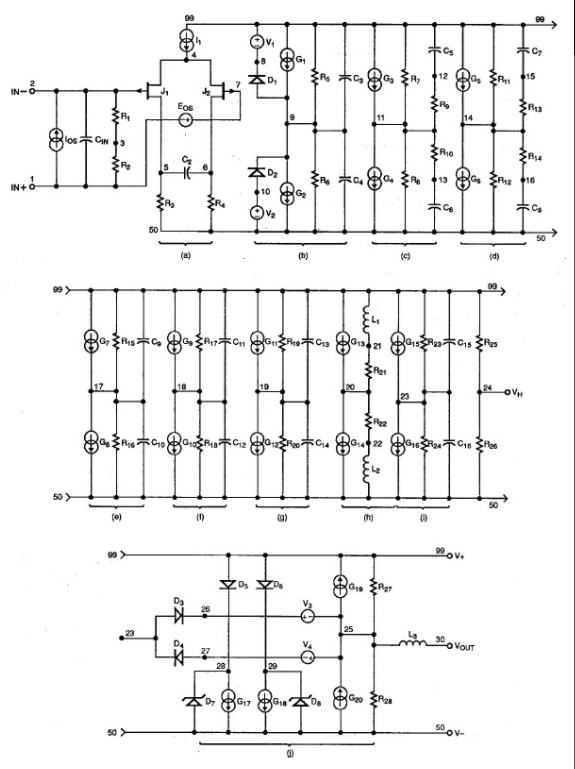
图6:OP-42宏模型远比Boyle模型复杂,需要更长的仿真时间,但其精度大幅提高
列表1:OP-42 SPICE宏模型网络列表
OP-42宏模型 © PMI 1990
SUBCKT OP-42 1 2 30 99 50
15.9 MHZ时的输入级和极点

53 MHZ时的极点

使用的模型
JX PJF模型(BETA=999.3E-6 VTO=-2.000 IS=8E-11)
DX模型 D(IS=1E-15)
DY模型 D(IS=1 E-15 BV=50)
ENDS OP-42
因此,图5中两个校正源的作用是在供电轨之间产生一个等于输出电流一半的单极性补偿电流。在SPICE中,因为难以实现绝对值VCCS,所以必须具有两个线性校正源——一个校正源对应半个输出电流周期。与每个源串联的二极管执行半波整流,
齐纳二极管确保当电流反向时,始终为每个源提供导电路径。所有这些附加元件最终形成了一个输出级模型,其直流行为非常接近实际电路的行为。
为了解决发射极跟随器输出级阻抗随频率升高的典型现象,宏模型内置一个输出电感,连接在中间输出节点和实际宏模型输出节点之间(参见图5)。可以通过在模型上使用容性负载来确定这个电感的值,经过不断试验和试错,直到过冲量与采用同样负载的实际运算放大器极为接近为止。
出色的运算放大器宏模型还必须具备短路电流限制特性,在图5中,通过使用二极管D3和D4以及电压源V3和V4,将前一个频率成形级的输出电压(VF)箝位到中间输出节点(V0)来实现限制。注意,在没有负载的情况下,前一级的信号始终等于理想的输出电压,并且输出级就像是具有有限输出阻抗的电压源。二极管和电压源的作用相当于箝位有效输出电阻上的压降。通过适当选择每个电压源,可以获得所需的输出限流。
由于新结构的主要目标是提高交流精度,因此该模型也必须正确表示共模行为。因此,建模团队选择PMI OP-42(JFET输入运算放大器)作为第一个实验对象,主要是因为Boyle模型无法正常仿真JFET输入级。虽然在测试整个模型之前,该团队必须计算出与JFET输入级有关的所有方程,但之后发现,从数学角度处理这个级相当容易,并不妨碍最终的宏模型结构开发。
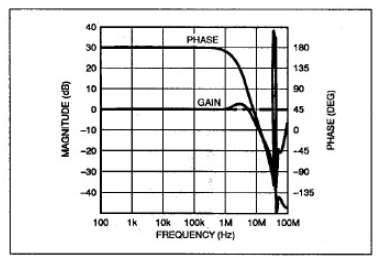
图7:以单位增益、反相配置连接OP-42时,增益响应在6MHz左右有一个小高峰;
2MHz之后,相位偏移急剧增加。
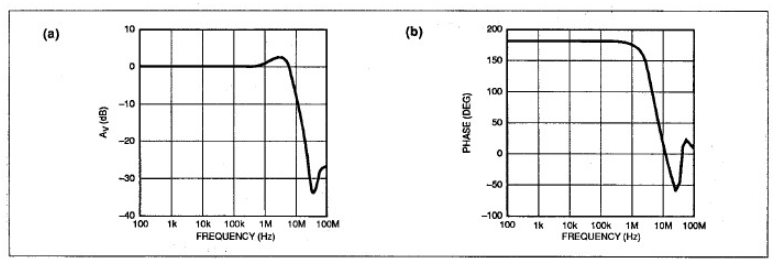
图8:采用新的宏模型,OP-42的仿真增益响应(a)与实际器件非常相似,在4MHz有一个小峰值。
相位响应(b)非常不错。这条曲线与实际器件的曲线非常接近。
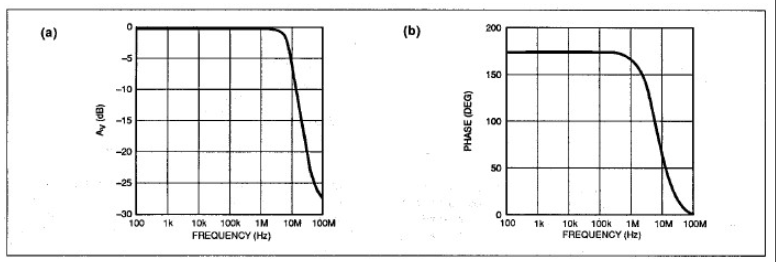
图9:OP-42的Boyle模型(a)在4MHz时,没有显示实际器件所具备的幅度峰值特性。
相位响应(b)也不是很准确,特别是在超过10MHz的区域。
图10:具有430pF电容负载的OP-42在500kHz、200mV峰值方波的驱动下显示过冲和欠冲
图6显示随之得出的结果。实际OP-42具有约10MHz的增益带宽乘积,以及50V/µs的对称压摆率。从该放大器的CMRR与频率关系曲线可以看出,该模型的共模增益级需要一个零点(约100kHz处)。
列表1所示为OP-42宏模型的网络列表,它有8个极点、2个零点,以及在共模增益级的100kHz处的一个零点。即使是一个相对稳定的放大器模型也需要这些极点和零点,以便准确地模拟实际器件在高频率下的增益和相位行为。
查看网络列表的输出级部分可知,开环输出电阻为45Ω。与输出端口串联的250nH电感可以补偿高频率下有效开环输出阻抗的上升。由二极管D3和D4以及电压源V3和V4组成的限流网络将最大输出电流箝位在约±30mA。
仿真精度比较
图7显示作为反相单位增益放大器连接的实际OP-42的增益和相位响应,该放大器具有1kΩ输入和反馈电阻,采用±15V电源供电。在闭环增益曲线上,可以看到一个小峰值(约2dB),在超过2MHz之后,相位偏移急剧增加。图8a和图8b显示在相同条件下,新OP-42宏模型的增益和相位响应。增益响应显示与实际电路具有相同的闭环峰值;相位响应与实际器件的相位响应几乎完全一样,至少达到10MHz。
图9a和9b显示采用Boyle模型时的输出曲线,从中可以明显看出Boyle模型在响应精度方面的缺陷。增益响应未出现2dB峰值,表明急剧滚降,在超过10MHz之后,结果非常不准确。Boyle模型的相位响应与实际电路的响应相去甚远。OP-42宏模型采用多个极零点补码,可以更准确地仿真实际电路的交流响应。

图11:采用新的宏模型仿真OP-42(采用430pF容性负载)的结果显示,该模型的输出级具有对称性
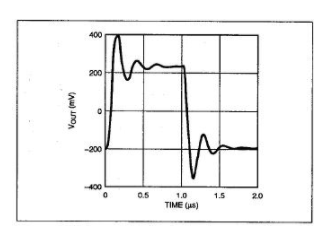
图12:采用Boyle模型仿真OP-42时,仿真了大约等量的过冲,但其振铃频率过低
图10显示在430pF容性负载下,测量的反相单位增益OP-42放大器的瞬态响应。对于400mVp-p输入信号,大约有75%的过冲和100%的欠冲。新的宏模型仿真结果(参见图11)显示大约115%的过冲和欠冲。这个仿真值与波形负半部的实际值相当接近,但与正半部的实际值不同。对于这种异常,给出的解释是:尽管新的宏模型的输出级完全对称,但所建模的运算放大器可能并非如此。OP-42实际上具有不对称、完全由NPN晶体管组成的输出级。所以,高频开环响应是可变的,具体取决于输出级是吸电流还是源电流。
Boyle配置也将运算放大器的输出级建模为完全对称的电压源,如图12所示,它在输出波形负半部的欠冲仿真并不正确。它在正半部的仿真与实际电路非常接近,但是振铃频率低于实际电路。
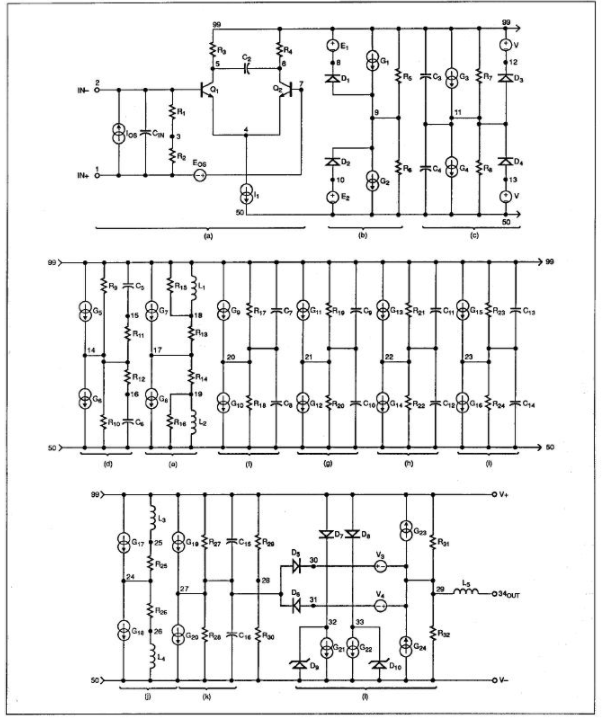
图13:除了多了一个增益级之外,OP-61的模型示意图与OP-42类似
列表2:OP-61 SPICE宏模型网络列表
OP-61宏模型 © PMI 1989
SUBCKT OP-61 1 2 34 99 50
300 MHZ时的输入级和极点
200MHZ时的极点

使用的模型
QX NPN模型(BF=1250)
DX模型 D(IS=1E-15)
DY模型 D(IS=1E-15 BV = 50)
ENDS OP-61
Boyle方法本身不支持对非对称输出级行为建模,很遗憾,这种新的宏模型也是如此。但是,这个缺陷是可以解决的。如果在生成模型的过程中发现过冲值与欠冲值不同,那么在输出电感相关计算中应使用两个值中较大的一个。然后,在容性负载下,该电感值将会产生最差情况下的过冲和欠冲结果。
执行时间比较
假设宏模型不存在收敛问题,那么SPICE进行操作点计算或生成直流转换曲线所需的时间很大程度上取决于网络列表中指定的电路元件数量。因此,新的OP-42宏模型的速度几乎比Boyle模型慢一半,需要进行2.27次迭代,才能得出最终的解决方案。对于交流分析案例,情况也是这样,新的宏模型的运行时间几乎是Boyle宏模型的两倍。但是,在仿真交流响应时,这两种模型需要的迭代次数基本是相同的。
由于所涉因素很多,很难评估瞬态分析需要多大的计算量。特别是,新的宏模型会展示比Boyle模型更多的细节。所以,仿真器必须使用更精细的时间步长,相应地执行更多的计算。但是,模型中大量的理想元件使得模型具有很好的收敛性能。所以,有时可以通过在单个时间步长内进行更多次迭代来加快分析速度,这样,仿真器可以保持粗略的时间步长,并减少回溯次数。
大多数SPICE仿真器将瞬变迭代次数默认为10。您可以在.OPTIONS部分将ITL4设置为一个更大的数值(比如40),以覆盖这个默认值。此外,将RELTOL放宽到0.01(默认值通常为0.001),通过略微降低准确性也可加快运行时间。这种降低是可行的,因为宏模型本身也只是一种近似法。但是,请注意,图11和图12是在RELTOL设置为0.001而不是0.01时生成的,所以曲线会更为准确。另一种加快瞬态分析速度的方法是使用GEAR积分,而不是梯形积分;但是,使用这种积分得出结果的振荡幅度要比实际结果低得多。
RELTOL使用0.01,ITL4和梯形积分使用40,OP-42宏模型的瞬变运行速度比Boyle慢3.64倍,且需要2.15倍迭代。仿真速度虽然大幅降低,但是可以接受,并且精度大大提高,足以抵消这种降低。
OP-61宏模型
OP-61是一种双极输入宽带精密运算放大器,典型的增益带宽积为200MHz(测试频率为1 MHz时),压摆率为40V/µs。图13所示的这种器件的模型比OP-42的模型稍微复杂一点。OP-61的共模抑制在比OP-42的CMRR低的频率下开始滚降,但在1MHz时,其值仍然非常可观,为80dB。网络列表(参见列表2)表明OP-61模型需要9个极点和2个零点来模拟开环频率响应,并且共模增益在40kHz时为零。
注意,这个模型在差分输入级和主增益级(参见图13c)之间有一个额外的增益级(图13中的级b),可以生成放大器主极点。这个特殊的模型需要额外的增益级,因为OP-61不能满足极限方程要求,该方程涉及双极性输入级的压摆率、开环增益和主极点频率(参见框1)。OP-61模型需要100dB开环增益和40V/µs压摆率,但其增益带宽积(以及由此得出的主极点频率)太高,无法由单个级生成所有开环电压增益。
所以,该模型使用两个增益级,共同提供所需的100dB增益。第一个增益级的增益为200;第二个为500。必须对第一个增益级箝位,以限制施加给第二个增益级中电压控制电流源的最大驱动电压。这个箝位操作会限制传递给补偿电容C5和C6的峰值电流,从而限制第二个增益级的最大dV/dt。
因为输入级的最大差分输出电压仅为51.6mV,所以第一个增益级必须提供较大增益。为了便于对电压源和二极管进行箝位,需要一个更大的电压。第一个增益级的200增益在摆动期间可以产生相对于Vh的±10.32V无阻尼电压,但是无论使用哪个供电轨,箝位电路都会将此值限制为约±5.0V。这种配置支持进行可靠箝位,即使电源电压低至±4.4V,这也导致所需压摆率为40V/µs。
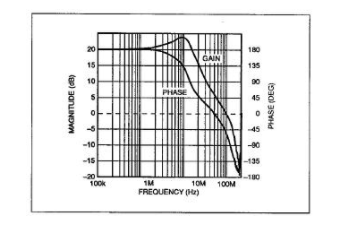
图14:将一个实际OP-61连接为反相放大器,增益为10时,增益响应在10MHz时显示达到3dB峰值。
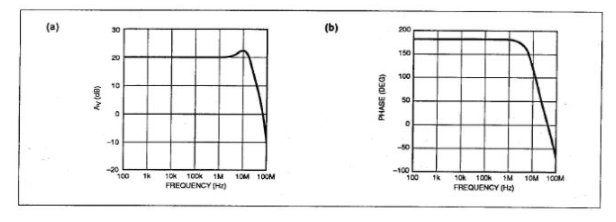
图15:OP-61宏模型的仿真增益(a)显示了在10MHz时的正确峰值。
此外,它在40MHz时的相位响应(b)与实际器件的响应仅偏差10°。

图16:实际OP-61连接为反相放大器,且增益为10,容性负载为207pF时,其瞬态响应不太对称。
输入信号为500kHz方波,峰值幅度为10mV。垂直标度为0.1 V/div,水平标度为0.2µs/div。
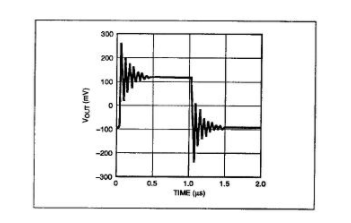
图17:OP-61宏模型仿真的瞬态响应非常接近实际器件的瞬态响应
仿真精度比较
图14显示了配置为反相放大器、增益为10的实际OP-61的增益和相位响应测量值。其中使用了一个1kΩ反馈电阻、一个100Ω输入电阻和±15V电源。在10MHz范围内,振幅响应出现约3dB的峰值,在10MHz以上,相位偏移急剧增加。对于这些响应,新的宏模型(参见图15a和15b)的测量值与OP-61非常一致。增益曲线显示,在稍高于10MHz的位置,出现了所需的增益峰值(稍微超出2dB)。相位响应精度也非常不错;在40MHz时,误差只有10°左右,可能在试验板由于寄生电容和其他物理效应导致的偏差范围内。因此,这个新的宏模型是一个可以预测OP-61性能的有用工具,甚至可以在评估试验板之前进行预测。
图16显示了OP-61的瞬态响应,看起来非常不稳定,但该器件正在驱动207pF容性负载。该波形显示过冲量和欠冲量之间存在一些不对称性(180%对比220%),但是OP-61和OP-42一样,并没有完全平衡的输出级结构。所选的输出电感(模型中的L5)在很大程度上决定了仿真的瞬态响应与实际响应之间的相似程度。事实上,图17所示的仿真产生了对称的过冲和欠冲(约150%),与图16相比稍低,但其振铃频率则稍高。这种差异对用户来说并不太重要。但是,如果这很重要,可以稍微增大输出电感的值,使仿真响应更接近实际器件响应。
通过与OP-42(没有OP-61的Boyle模型)比较,您可以大致了解新OP-61模型的性能。在计算直流偏置点时,OP-61宏模型比OP-42宏模型更快。但是,进行交流响应仿真时,OP-61宏模型则比OP-42宏模型慢1.18倍。
进行瞬态响应仿真时,OP-61宏模型所花的时间是OP-42宏模型的1.76倍,迭代次数是OP-42的1.56倍。在这方面,您应该记住,瞬态运行的仿真时间随着输出振荡的加剧而增加。所以,直接比较OP-42和OP-61的执行时间并不公平,因为OP-42的响应比OP-61更平缓。
仿真目标在不断改变
计算机模型用于对一些物理现象进行准确建模;现象越复杂,计算机执行必要计算所需的时间就越长。Boyle运算放大器模型的目标是减少需要仿真的非线性元件的数量,从而将运行时间缩短至可接受的水平。Boyle模型在建立时并未考虑到最终准确性,但它可以正确预测运算放大器的低频性能,对于当时的低性能器件来说,结果是令人满意的。
但是如今,对更高性能的需求日益增长,如果可以准确预测新器件的性能,则可以帮助避免设计错误,以免在生产阶段因纠正这些错误耗费大量成本。所以,准确的高频性能建模至关重要,在这一领域,Boyle模型无法满足需求。本文所描述的经过改进的运算放大器宏模型不仅能比Boyle模型更准确地仿真运算放大器的高频响应和瞬态行为,还不会耗费过多的CPU时间。如今,拥有了强大的桌面工作站,建模的重点是提高仿真精度,而不是缩短执行时间。所以,新的宏模型提供了良好的折衷方案。
这个新的宏模型的最大限制因素在于:为了保证SPICE的兼容性,该模型必须以包含实际电路元件的网络列表的形式编写。一些新仿真器(如ADI公司的Saber)允许您用专门的编程语言来定义模型,无需采用电路类型架构。Saber建模语言称为Mast,与C语言非常类似,可以有效管理内部变量。例如,允许完全用数学方法来描述新的宏模型的输出级。Saber模型不需要SPICE模型用来对输出级电流实施校正的所有二极管和额外源。输出级的定义方程会直接考虑从模型输出端获取的任何负载电流。在不久的将来,新的宏模型很可能会在Saber中实现。
参考文献
1. Boyle, Graeme R., et al, “Macromodeling of Integrated Circuit Operational Amplifiers,” IEEE Journal of Solid State Circuits, Vol. sc-9, no. 6, December, 1974.
2. Gray, Paul R. and Robert G. Meyer, Analysis and Design of Analog Integrated Circuits, John Wiley & Sons, 1977, pp 159-161.
3. ibid, pp 175-177.
4. Laurence W. Nagel,“SPICE2:A Computer Program to Simulate Semiconductor Circuits,“ U.C.Berkeley Memorandum No. M520, May, 1975.
 电子发烧友App
电子发烧友App




















评论