所有模数转换器(ADC)都有一定量的输入参考噪声,建模为与无噪声ADC输入串联的噪声源。不要将折合到输入端的噪声与量化噪声混淆,量化噪声仅在ADC处理时变信号时才有意义。在大多数情况下,输入噪声越少越好;然而,在某些情况下,输入噪声实际上有助于实现更高的分辨率。
折合到输入端的噪声(代码转换噪声)
实用型ADC在许多方面都与理想ADC不同。折合到输入端的噪声肯定与理想值有所不同,其对整个ADC传递函数的影响如图1所示。随着模拟输入电压的增加,“理想”ADC(如图1a所示)保持恒定的输出代码,直到到达转换区域,此时它会立即跳转到下一个值,一直保持在那里,直到到达下一个转换区域。理论上完美的ADC具有零代码转换噪声,转换区域宽度等于零。实际ADC具有一定数量的代码转换噪声,因此具有有限的转换区域宽度。图1b显示了代码转换噪声的宽度约为<>个最低有效位(LSB)峰峰值的情况。
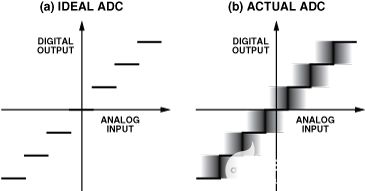
图1.代码转换噪声(折合到输入端的噪声)及其对ADC传递函数的影响。
在内部,所有ADC电路都会因电阻噪声和“kT/C”噪声而产生一定量的均方根噪声。这种噪声甚至对于直流输入信号也存在,它解释了代码转换噪声,现在通常称为折合到输入端的噪声。折合到输入端的噪声通常通过检查多个输出样本的直方图来表征,而ADC的输入则保持在直流值不变。大多数高速或高分辨率ADC的输出是代码分布,通常以直流输入的标称值为中心(见图2)。
为了测量折合到输入端的噪声量,ADC的输入要么接地,要么连接到高度去耦的电压源,并收集大量输出样本并绘制为直方图(如果输入标称值为零伏,则称为接地输入直方图)。由于噪声近似于高斯,因此可以计算的直方图σ的标准偏差对应于有效输入均方根噪声。有关如何根据直方图数据计算σ值的详细说明,请参阅进一步阅读 6。通常的做法是用LSBs均方根来表示这种均方根噪声,对应于以ADC满量程输入范围为基准的均方根电压。如果模拟输入范围表示为数字或计数,则输入值(如σ)可以表示为LSB数量的计数。
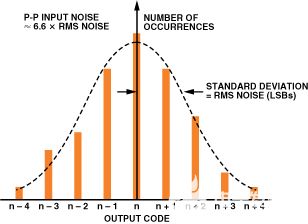
图2.折合到输入端的噪声对具有少量DNL的ADC的ADC接地输入直方图的影响。
虽然ADC固有的微分非线性(DNL)会导致与理想高斯分布的偏差(例如,图2中可以看到一些DNL),但它至少应该近似于高斯分布。如果存在显著的DNL,则应计算几种不同直流输入电压的σ值,并将结果取平均值。如果代码分布明显非高斯分布,例如大而明显的峰值和谷值,这可能表明ADC设计不佳,或者更有可能表明PCB布局不佳、接地技术不良或电源去耦不当(见图3)。另一个问题迹象是,当直流输入扫过ADC输入电压范围时,分布宽度发生剧烈变化。
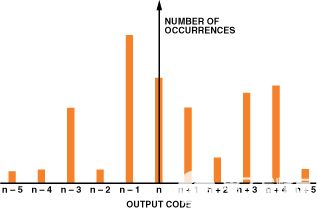
图3.接地输入直方图,用于设计不良的ADC和/或布局、接地或去耦不良的情况。
无噪声(无闪烁)代码分辨率
ADC的无噪声码分辨率是分辨率位数,超过该位数就不可能明确分辨单个代码。这种限制是由于与上述所有ADC相关的有效输入噪声(或折合到输入端的噪声)造成的,通常表示为LSBs均方根单位的均方根量。乘以系数6.6可将均方根噪声转换为峰峰值噪声的有用度量,即可以识别代码的实际不确定性,以LSB的峰峰值表示。由于N位ADC的总范围(或跨度)为2N因此,LSB,无噪声计数的总数等于:
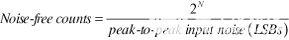 |
(1) |
通过计算以 2 为底的对数,可以将无噪声计数的数量转换为无噪声(二进制)代码分辨率,如下所示:
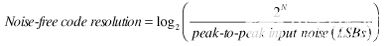 |
(2) |
无噪声码分辨率规范通常与高分辨率Σ-Δ测量ADC相关。它通常是采样速率、数字滤波器带宽和可编程增益放大器(PGA)增益(因此输入范围)的函数。图4所示为典型表格,取自AD7730 Σ-Δ型ADC的数据手册。
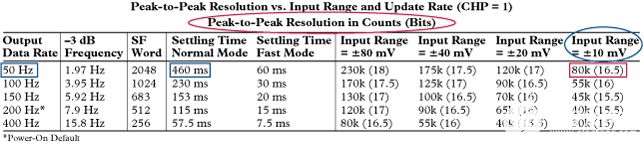
图4.AD7730 Σ-Δ型ADC的无噪声代码分辨率。
请注意,对于50 Hz的输出数据速率和±10 mV的输入范围,无噪声码分辨率为16.5位(80,000个无噪声计数)。这些条件下的建立时间为460 ms,使该ADC成为精密电子秤应用的理想选择。适用于精密测量应用的高分辨率Σ-Δ型ADC的大多数数据手册中都提供了此类数据。
满量程范围与均方根输入噪声(而不是峰峰值噪声)之比有时用于计算分辨率。在这种情况下,使用术语有效分辨率。请注意,在相同条件下,有效分辨率大于通过日志进行无噪声代码解析2(6.6),或大约 2.7 位。
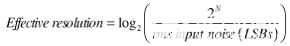 |
(3) | |
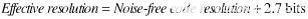 |
(4) |
一些制造商更喜欢指定有效分辨率而不是无噪声代码分辨率,因为这会产生更多的位数——用户应仔细检查数据手册,以确保实际指定了哪个。
数字平均可提高分辨率并降低噪声
折合到输入端的噪声的影响可以通过数字平均来降低。考虑一个16位ADC,它具有15个无噪声位,采样速率为100 kSPS。对每个输出样本的不变信号进行两次测量平均,可将有效采样速率降低到50 kSPS,并将SNR提高3 dB,无噪声位数提高到15.5。对每个输出样本进行四次测量的平均值可将采样速率降低至25 kSPS,并将SNR提高6 dB,无噪声位数提高至16 dB。
我们可以更进一步,平均每个输出 16 次测量;输出采样速率降低到6.25 kSPS,SNR又增加了6 dB,无噪声位数增加到17 dB。平均中的算术精度必须对更多的有效位进行,以获得额外的“分辨率”。
平均过程还有助于消除ADC传递函数中的DNL误差。对于ADC在量化级别k缺少代码的简单情况,可以说明这一点。即使由于 DNL 误差较大而缺少代码 k,两个相邻代码 k – 1 和 k + 1 的 平均值等于 k。
因此,该技术可以有效地用于增加ADC的动态范围,但代价是总输出采样速率和额外的数字硬件。还应注意的是,平均不会校正ADC固有的积分非线性。
现在,考虑一个ADC的情况,它具有极低的输入参考噪声,无论采集多少样本,直方图都会显示单个代码。数字平均对这款ADC有什么作用?这个答案很简单——它什么也做不了!无论平均多少样本,答案都是一样的。但是,一旦向输入信号添加了足够的噪声,使直方图中有多个代码,平均方法就会再次开始工作。因此,有趣的是,一些少量的噪声是好的(至少就平均方法而言);但是,输入端的噪声越多,实现相同分辨率所需的平均就越多。
不要将有效位数 (ENOB) 与有效分辨率或无噪声代码分辨率混淆
由于术语的相似性,有效位数和有效分辨率通常被假定为相等。事实并非如此。
有效位数(ENOB)来自ADC被满量程正弦波输入信号激励时对ADC输出的FFT分析。计算所有噪声和失真项的平方根和(RSS)值,并将信号与噪声和失真的比定义为SINAD或S/(N+D)。完美N位ADC的理论信噪比由下式给出:
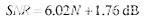 |
(5) |
ENOB的计算方法是将ADC计算的SINAD代入式中的SNR,并求解方程N。
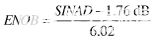 |
(6) |
用于计算SINAD和ENOB的噪声和失真不仅包括折合到输入端的噪声,还包括量化噪声和失真项。SINAD和ENOB用于测量ADC的动态性能,而有效分辨率和无噪声代码分辨率用于测量ADC在基本直流输入条件下的噪声,其中量化噪声不是问题。
使用噪声抖动来增加ADC的无杂散动态范围
无杂散动态范围(SFDR)是均方根信号幅度与峰值杂散频谱分量的均方根值之比。在高速ADC中最大化SFDR的两个基本限制是前端放大器和采样保持电路产生的失真;以及由ADC编码器部分传递函数中的非线性产生的。实现高SFDR的关键是最小化两个非线性源。
ADC外部无需采取任何措施,以显著降低其前端引起的固有失真。但是,ADC编码器传递函数中的差分非线性可以通过正确使用抖动(有意与模拟输入信号相加的外部噪声)来降低。
抖动可用于在某些条件下改善ADC的SFDR(参见延伸阅读2-5)。例如,即使在完美的ADC中,量化噪声和输入信号之间也存在一定的相关性。这种相关性会降低ADC的SFDR,特别是当输入信号是采样频率的精确子倍数时。将大约1/2 LSB rms的宽带噪声与输入信号相加,往往会使量化噪声随机化,并将这种影响降至最低(见图5a)。然而,在大多数系统中,已经位于信号顶部的噪声(包括ADC的输入参考噪声)消除了对额外抖动噪声的需求。将宽带均方根噪声水平提高到大约<>LSB以上将按比例降低SNR,并且不会带来额外的改善。
已经开发了其他方案,使用大量抖动噪声来随机化ADC的传递函数。图5b示出了包含驱动DAC的伪随机数发生器的抖动噪声源。该信号从ADC输入信号中减去,然后以数字方式添加到ADC输出中,因此不会显著降低SNR。然而,这种技术的固有缺点是,必须减小输入信号摆幅,以防止随着抖动信号幅度的增加而过驱ADC。请注意,虽然该方案改善了ADC编码器非线性产生的失真,但并未显著改善其前端产生的失真。
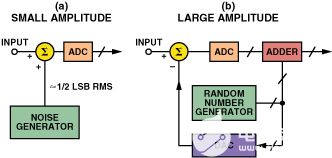
图5.使用抖动随机化ADC传递函数。
另一种更容易实现的方法(特别是在宽带接收器中)是在目标信号频带之外注入窄带抖动信号,如图6所示。通常,在直流附近的频率范围内没有信号分量,因此该低频区域通常用于这种抖动信号。抖动信号的另一个可能位置略低于fS/2.抖动信号相对于信号带宽仅占用很小的带宽(通常几百kHz的带宽就足够了),因此SNR不会发生明显的下降,就像抖动是宽带时一样。
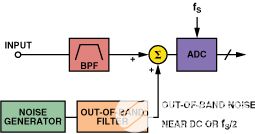
图6.注入带外抖动以改善ADC SFDR。
量程流水线ADC,例如6645位、14 MSPS ADC(见图105)AD7,在ADC范围内的特定代码转换点处发生非常小的差分非线性误差。AD6645内置一个5位ADC (ADC1),后接一个5位ADC2和一个6位ADC3。唯一显著的DNL误差发生在ADC1转换点,第二级和第三级DNL误差最小。有 2 个5= 32个与ADC1相关的决策点,每68.75 mV发生一次(29= 512 LSB),适用于 2.2V 满量程输入范围。图8显示了这些非线性的夸张表示。
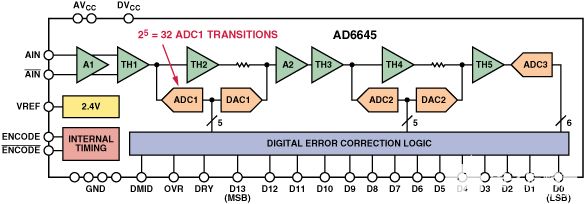
图7.AD6645 14位、105 MSPS ADC简化框图
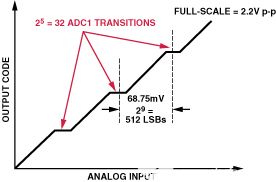
图8.AD6645子量程点DNL误差(夸大)。
当模拟输入高达约200 MHz时,与编码器产生的失真分量相比,AD6645前端产生的失真元件可以忽略不计。也就是说,AD6645传递函数的静态非线性是SFDR的主要限制。
目标是选择适当数量的带外抖动,以便这些小DNL误差的影响在整个ADC输入范围内随机化,从而降低平均DNL误差。实验确定,使峰峰值抖动噪声覆盖大约两个ADC1转换可以最好地改善DNL。随着噪声水平的提高,DNL没有显着改善。两个ADC1转换覆盖1024 LSB的峰峰值,或大约155 (= 1024/6.6) LSB rms。
图9所示的第一个图显示了输入信号范围一小部分的无抖动DNL,包括两个间隔为68.75 mV (512 LSB)的子量程点。第二张图显示了添加(后来滤除)155 LSB的均方根抖动后的DNL。此抖动量对应于大约 –20.6 dBm。请注意 DNL 的显著改进。
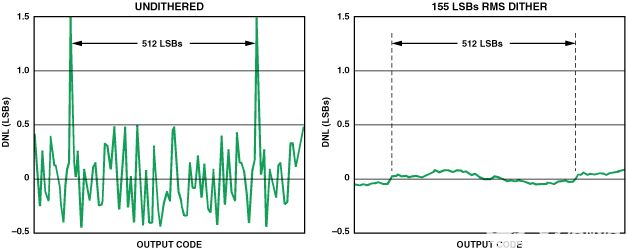
图9.AD6645 DNL图,无抖动和带抖动。
抖动噪声可以通过多种方式产生。例如,可以使用噪声二极管,但简单地放大宽带双极性运算放大器的输入电压噪声可提供更经济的解决方案。这种方法将在别处(延伸阅读3、4和5)中详细描述,本文将不讨论。
使用深(10,1,048点)FFT时,使用带外抖动可获得的SFDR显著改善,其中AD576以6645 MSPS采样–35 dBm、30.5 MHz信号。请注意,没有抖动的SFDR约为80 dBFS,而有抖动的SFDR约为92 dBFS,这是108 dB的实质性改进!
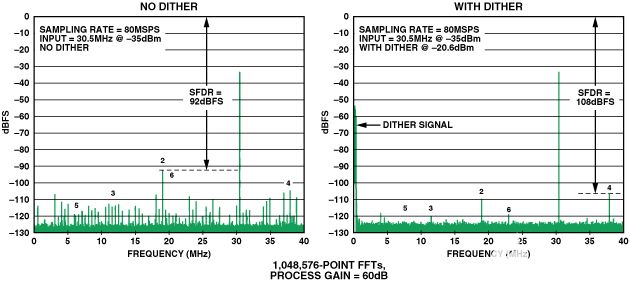
图 10.FFT图显示AD6645 SFDR,没有抖动,也没有使用抖动。
ADI公司于6645年推出的AD2000 ADC直到最近才代表了SFDR性能的极致。自推出以来的几年中,工艺技术和电路设计的改进使ADC的性能更加提高,例如AD9444(14位,80 MSPS)、AD9445(14位、105 MSPS和125 MSPS速度等级)和AD9446(16位、80 MSPS和100 MSPS速度等级)。 这些ADC具有非常高的SFDR(对于90 MHz满量程输入信号,通常大于70 dBc)和低DNL。尽管如此,添加适当的带外抖动信号可以改善某些输入信号条件下的SFDR。
图11对AD9444的FFT图进行了建模,有抖动和不带抖动。可以看出,在给定的输入条件下,增加抖动可使SFDR提高25 dB。数据是使用ADIsimADC获取的™程序和AD9444模型。
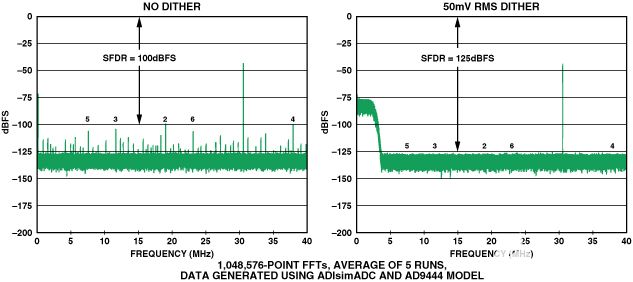
图 11.AD9444 14位、80MSPS ADC;fS= 80 兆字节, f在= 30.5 MHz,信号幅度 = –40 dBFS。
尽管图10和图11所示的结果相当引人注目,但不应假设增加带外噪声抖动总能改善ADC在所有条件下的SFDR。我们重申,抖动不会改善ADC前端电路的线性度。即使使用近乎理想的前端,抖动的影响也将高度依赖于输入信号的幅度和抖动信号本身的幅度。例如,当信号接近ADC的满量程输入范围时,传递函数的积分非线性可能成为决定SFDR的限制因素,抖动将无济于事。无论如何,都应仔细研究数据手册——在某些情况下,可能会显示抖动和未抖动数据,以及幅度和带宽建议。抖动可能是较新的中频采样ADC的内置功能。
总结
在本讨论中,我们考虑了所有ADC通用的折合到输入端的噪声。在精密、低频测量应用中,通过使用较低的采样速率和额外的硬件对ADC输出数据进行数字平均,可以降低这种噪声的影响。虽然这种平均过程实际上可以提高ADC的分辨率,但积分非线性误差并没有降低。只需少量的输入参考噪声即可通过平均技术提高分辨率;然而,使用增加的噪声需要在平均值中有更多的样本,因此达到了收益递减点。
在某些高速ADC应用中,增加适量的带外噪声抖动可以改善ADC的DNL并提高其SFDR。然而,抖动在改善SFDR方面的有效性在很大程度上取决于所考虑的ADC的特性。
审核编辑:郭婷
 电子发烧友App
电子发烧友App
























评论