滤波器设计的逼近方法 - Butterworth, Chebyshev, Elliptic
引言
在学习滤波器设计时,书本上往往直接甩出滤波器的传递函数公式,让人摸不着头脑,到底这些传递函数公式是如何得来的呢?一般文章中也绝口不提其原理是什么,难道这背后是否有什么玄机,是不是隐藏着什么神秘的东西!
带着疑问梳理了巴特沃斯(Butterworth)、切比雪夫(Chebyshev)、椭圆函数(Elliptic Function, Cauer)滤波器,终于对滤波器综合和设计内容有了比较系统的理解。如果大家有兴趣对这部分内容感兴趣可以阅读《威廉·卡尔(Wilhelm Cauer)的生活和工作》这篇文章,其中卡尔的网络综合纲领列出了滤波器综合的3个问题,即
- 1, 可实现性(realizability)
- 2, 近似(approximation)
- 3, 实现与等价(realization and equivalence)
实际上这三个问题中第一个可实现性问题在当时已经被解决了,即 正实函数(Positive-real function, PR, PRF) 可以被无源电路实现,随着时代发展,这部分内容已经被归入到信号与系统中。
现在滤波器设计类书籍中讨论最多的是第三个问题,即实现与等价,比如随着计算机发展,我们还是沿着模拟滤波器的设计思路在设计数字滤波器,并且在不同平台中实现,如何让资源最小,速度最快等等方向发展;另外往高频方向发展就引出了微波射频滤波器,如微带滤波器,腔体滤波器等等。现在工程中滤波器设计也主要集中在这一方面;有源器件发展的进步也丰富了滤波器设计。
现在关注最少的就是没有被提及的第二个问题,即近似(逼近,Approximation),滤波器近似可以说不是工程师的强项,因为这涉及到太多太复杂的数学知识,从滤波器名字可以看出,这里用到了多少数学知识:
| 滤波器类型 | 相关人物 | 国籍 | 头衔 |
|---|---|---|---|
| 巴特沃斯滤波器 | 巴特沃斯 | 英国 | 物理学家 |
| 切比雪夫滤波器 | 切比雪夫 | 俄罗斯 | 数学家 |
| 椭圆函数滤波器 | 雅可比 | 德国 | 数学家 |
| 卡尔 | 德国 | 数学家 | |
| 贝塞尔滤波器 | 贝塞尔 | 德国 | 数学家 |
| 勒让德滤波器 | 勒让德 | 法国 | 数学家 |
| 高斯滤波器 | 高斯 | 德国 | 数学家 |

可以看到一票的数学家,这方面发展现在主要集中在数学领域,比如逼近论就是数学的一个分支。
本文并不会严格的对数学公式进行推导,只是从工程师角度去直观理解滤波器设计所用的逼近方法,让人不再对滤波器设计存在盲区和疑惑。
另外下述讨论的滤波器设计逼近方法都是针对低通滤波器而言。
下图是对滤波器综合设计流程的梳理:
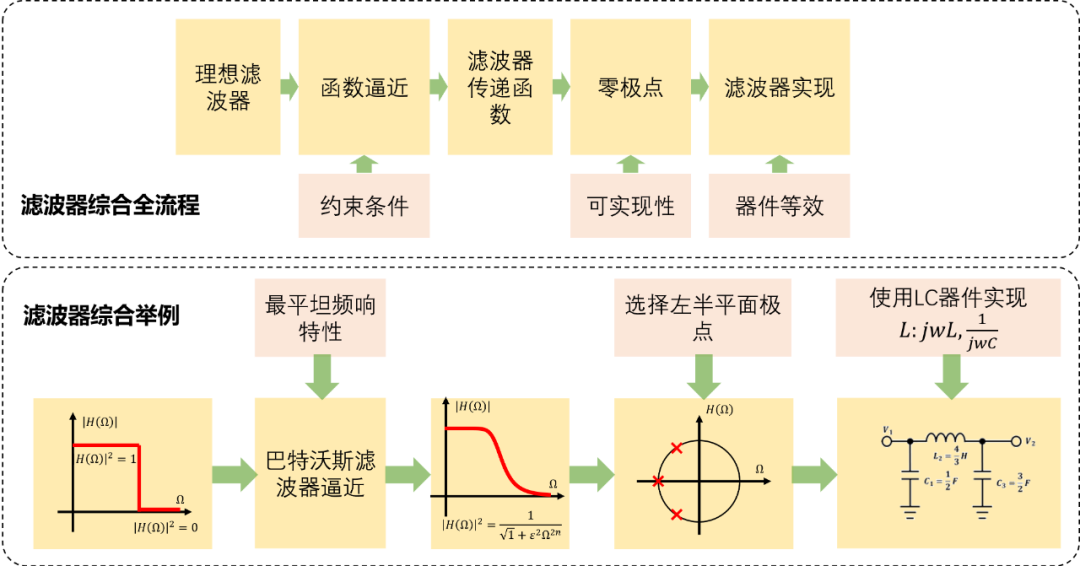
在滤波器逼近中最重要的是一步就是确定 约束条件 ,通俗一点讲就是提指标。下述滤波器逼近中单独将约束条件作为一个小结来说明。
特征函数(The Characteristic Function)
在电路中,历史上滤波器传递函数定义是:
由电压转到功率:
再由功率反射,得到反射系数,即反射到信号源的功率和输入总功率的比值:
联立(1),(2)得到:
令,得到
这里的就是 特征函数 。
特征函数有个好处是它只关注滤波器形状本身,并不关心滤波器的这个低频分量1,从而简化了计算,以下我们对滤波器函数的逼近最终都逼近到特征函数为止。
滤波器的衰减用如下公式计算,单位为dB:
现在滤波器设计中我们往往使用如下传递函数表示幅频响应:
注意它的dB形式和衰减的dB形式函数图像沿着横坐标镜像对称。
巴特沃斯滤波器逼近
巴特沃斯滤波器是具有最平坦频响特性的滤波器,如何理解这句话?在低通滤波器中,最平坦是指0频率处有最平坦特性,假设特征多项式为,其中为截止频率处的最大衰减量。
约束
由前面可知要实现一个可以综合的网络,首先我们要找到一个正实函数来逼近所需要的特性,要满足0频率处由最平坦特性,那么要求其:
- 1, 是一个阶多项式(可实现性)
- 2, (低通定义,在频率为0的位置无衰减)
- 3, (低通定义,截止频率在1)
- 4, 在0频率处各阶导数为0(在最低频率处具有最平坦特性)
函数逼近
由以上约束条件1,我们定义多项式为:
由约束条件2,得到:
由约束条件4,我们求其1阶导数:
并且让等于0,得到:
同理我们让其2阶导数为0,得到:
一直到第阶导数为0,得到:
这时不能再求导,因为再求导就会使得,那么就不是一个阶多项式了。 到这里特征多项式变为:
由约束条件3,得到:
最终得到巴特沃斯滤波器特征函数:
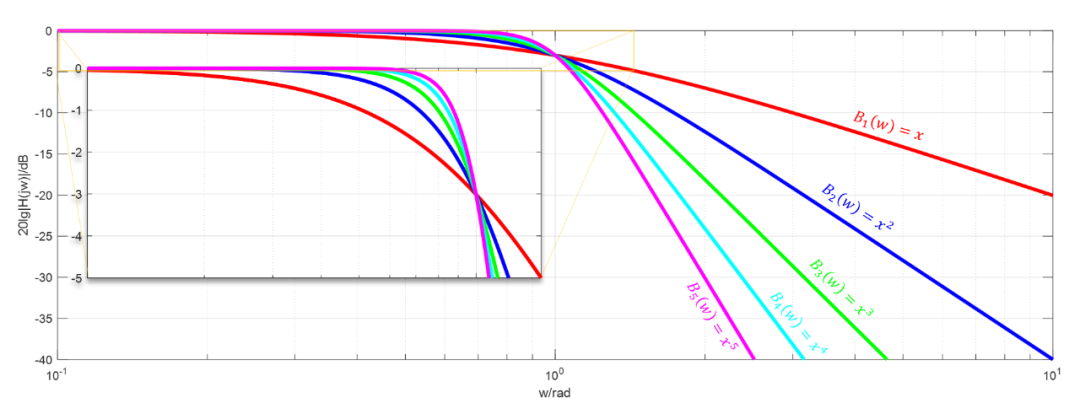
将巴特沃斯滤波器的幅频响应函数重写如下:
扩展
若我们想要得到处具有最平坦响应的低通滤波器,那么特征函数应该是什么样呢?
照例还是写下约束条件:
- 1, 是一个阶多项式(可实现性)
- 2, (低通定义,在频率为0的位置无衰减)
- 3, (低通定义,截止频率在1)
- 4, 在1/2频率处各阶导数为0(在最低频率处具有最平坦特性)
m阶导数等于0,且,且,得到个方程的方程组:
设,则有
解得:,最终得多项式为:
设,则有
解得:
最终得多项式为:
绘制5阶和7阶频响曲线如下:
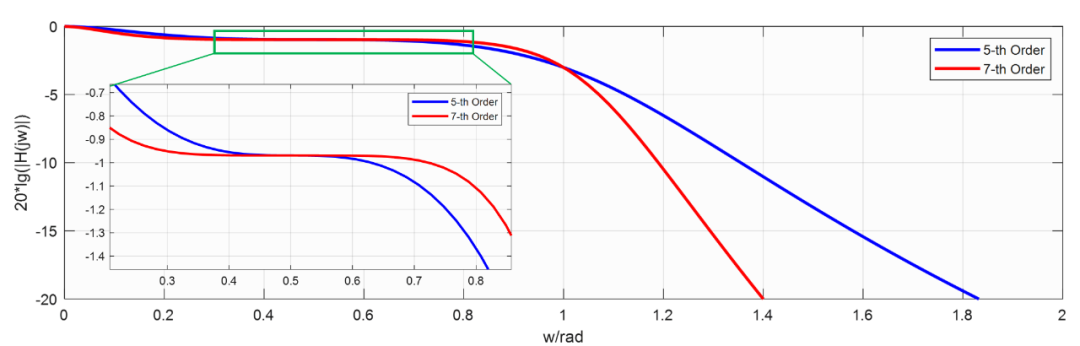
从频响曲线可以看出,在处有最大平坦特性,在这里我们综合出了一种特殊的滤波器!
比较这种B0p5(暂且叫做这个B0p5)滤波器和传统的巴特沃斯滤波器特性,有图有真相(图中比较位置将巴特沃斯滤波器频响往下移动并和B0p5重合,方便比较):
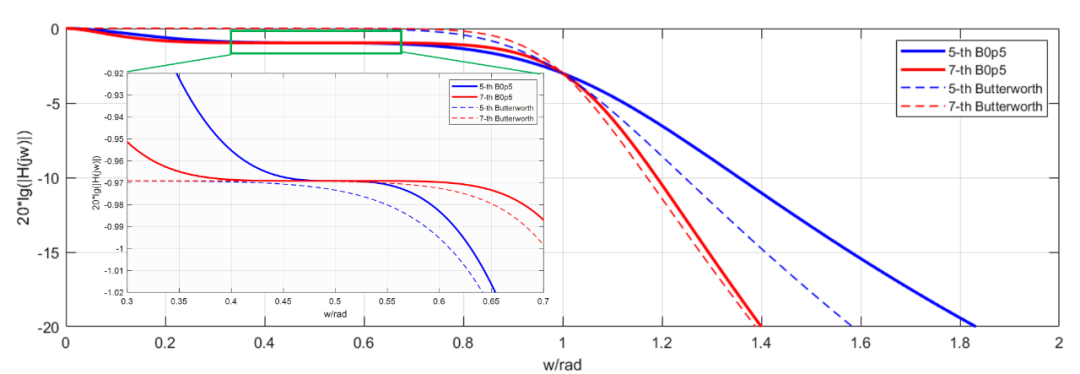
结果显示对于高阶,B0p5和普通巴特沃斯在高频抑制方面基本没有太大区别,区别在于快接近截止频率处B0p5要更为平坦,但是其代价就是牺牲了插损,差不多有1dB!有得必有失。
切比雪夫滤波器逼近
实际应用巴特沃斯滤波器的过程中,有没有发现一个问题,即巴特沃斯滤波器在截止频率附近的衰减都比较大,比如要滤除一个点频测试源的3次谐波,那么截止频率设计值要比实际有用信号频率值要高很多才不至于将我们关心的基波频率衰减很多。这也从侧面反应了巴特沃斯滤波器的一个缺点是为了保证0频率附近的平坦性,牺牲了其他频率的插损。尤其频率越高插损越大。
所以为了解决这个问题,人们改变了滤波器综合思路,不再去强调某一个点的特性,我们关注一个频段的特性,这也就是我们将要介绍的切比雪夫滤波器综合所要讨论的内容。
切比雪夫滤波器特性是通带范围内具有等纹波特性。假设特征多项式为,其中为通带纹波。
约束
由前面可知要实现一个可以综合的网络,首先我们要找到一个正实函数来逼近所需要的特性,要满足在通带内具有等纹波特性,那么要求其:
- 1, 是一个阶多项式(可实现性)
- 2, (低通定义,截止频率在1)
- 3, 在通带内摆动幅度在内(通带内等纹波特性)
- 4, 是奇函数如果为奇数; 是偶函数如果为偶数(可实现性,方便实现)
函数逼近
这里为了简单起见,只对进行讨论,其他阶数的任意阶滤波器都可以用类似的方法去推导。 首先我们由约束2,3和4绘出阶滤波器的的大致函数图像(阶函数具有个过0点):
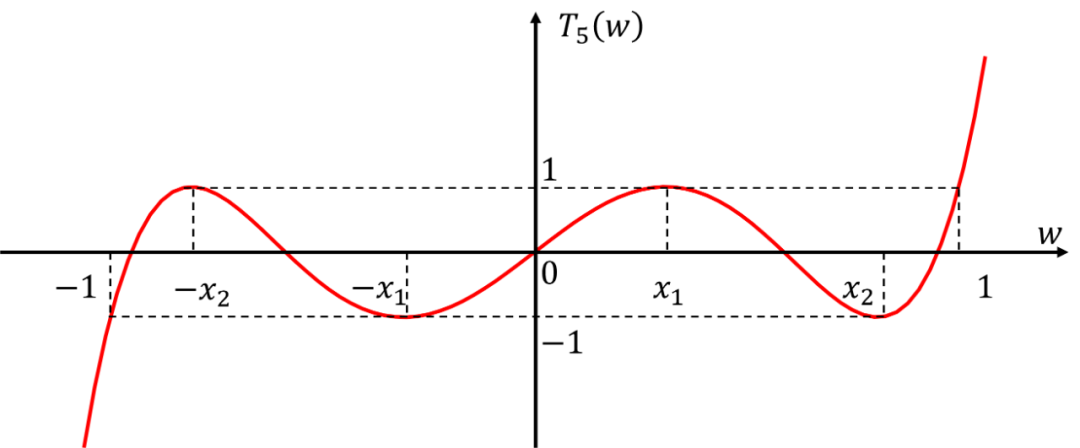
由约束1,令特征多项式为一个5次多项式:
若对这个方程求导,则得到一个4次方程,这个方程有4个根,由上述曲线极值点位置,可以得到这4个根,则列出第一个方程:
为了再和这些根扯上关系,绘出的函数图像
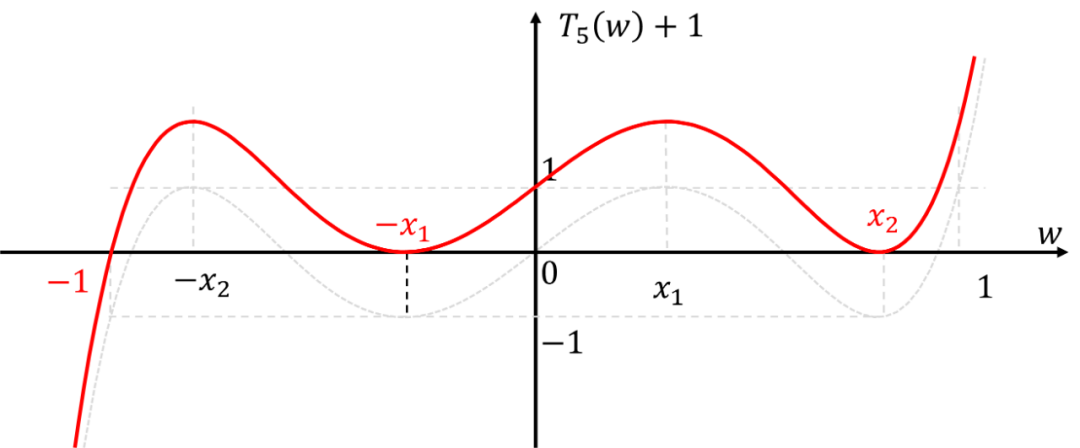
那么依据过0点位置,我们又可以得到一组方程:
这里要注意,由于曲线在拐弯的位置是有两个重根的,上式验算下方程的方次也可以推算出来。 同理,我们绘出的函数图像
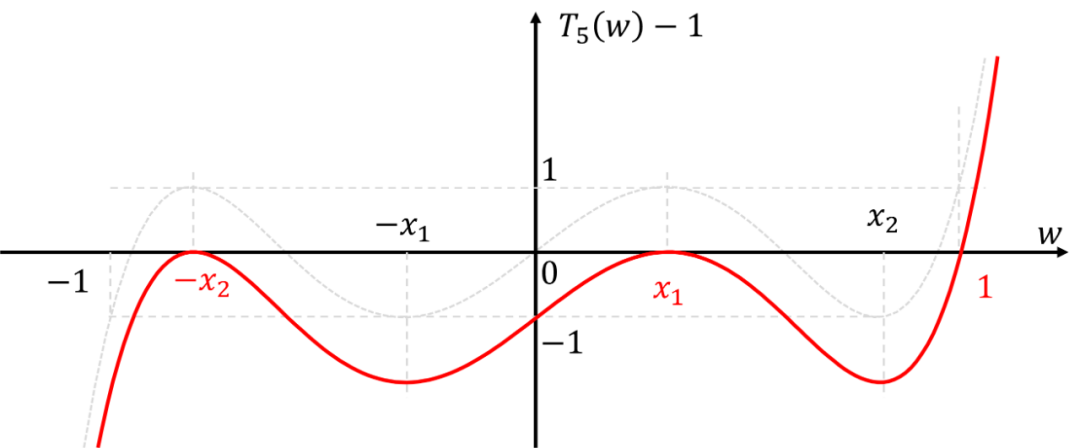
那么依据过0点位置,我们还可以得到一组方程:
将(8)和(9)左右相乘得到:
将(7)和(10)联立得到:
式(11)变形如下:
上式微分方程可以通过两边积分,得到:
于是得到时众所周知的切比雪夫函数:
对于其他阶数的切比雪夫滤波器,可以用同样的办法,最终得到阶切比雪夫函数为:
另外,对于这个公式比较严谨的推导见译文《切比雪夫逼近方法》。
扩展
假设我们不关心低通滤波器的低频第一个纹波,而是让低频到之间在之间等纹波,低频之间有最大值,那么应该如何进行函数逼近呢? 照例列出约束条件:
- 1, 是一个阶多项式(可实现性)
- 2, (低通定义,截止频率在1)
- 3, 在通带内摆动幅度在内(规定的通带内等纹波特性)
- 4, 是奇函数如果为奇数; 是偶函数如果为偶数(可实现性,方便实现)
PS. 这里暂时讨论偶数阶情况,具体的;奇数阶情况非常复杂,留着以后讨论。
则特征多项式为:
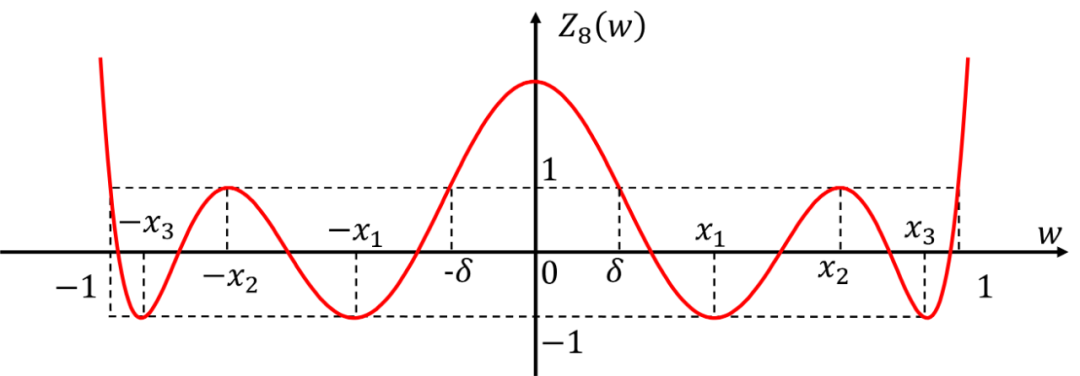
同样的对其进行求导得到:
然后计算,得到:
然后计算,得到:
同样将上式左右两边相乘:
将微分方程代入上式:
整理得到:
其中
所以最终结果为:
不同下绘图:
!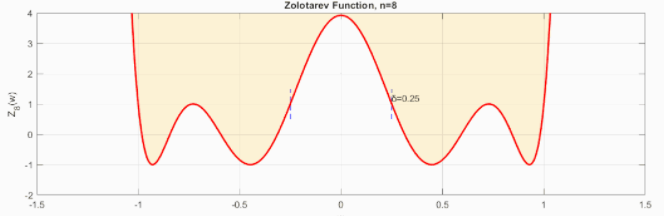
实际上这种滤波器名叫Achieser–Zolotarev滤波器或Zolotarev滤波器,在数字滤波器和微波滤波器中有应用。
椭圆函数滤波器逼近
由[模拟无源滤波器设计(六)-Chebyshev滤波器设计详解]可知逆切比雪夫滤波器"具有最平坦的通带频率响应,阻带具有等纹波特性",而同样具有最平坦通带响应的巴特沃斯滤波器,同样的阶数,那么为什么逆切比雪夫滤波器过渡带如此陡峭呢,究其原因就是因为逆切比雪夫滤波器的零点不在无穷远,它以牺牲无穷远处的衰减为代价换来了陡峭的过渡带。
那么沿着同样的思路,对于切比雪夫滤波器具有的无穷远处的极点,我们是否也可以将其移动到有限位置,从而让过渡带更加陡峭呢,答案是肯定的,这就是这一节所介绍的椭圆函数滤波器。
椭圆函数滤波器是通带和阻带都具有等纹波特性的滤波器。假设特征多项式为,其中为通带纹波。
约束
由前面可知要实现一个可以综合的网络,首先我们要找到一个正实函数来逼近所需要的特性,要满足在通带和阻带内都具有等纹波特性,那么要求其:
- 1, 是阶的两个有理数多项式之比(可实现性)
- 2, (自逆性,方便实现)
- 3, 是奇函数如果为奇数; 是偶函数如果为偶数(可实现性)
- 4, 的所有个零点都在频带内,所有个极点都在带外(等纹波特性)
- 5, 在通带范围摆动幅度在内(通带内等纹波特性)
- 6, (低通定义,截止频率在1)
- 7, 在阻带范围摆动幅度在内,其中和都在范围内(阻带内等纹波特性)
函数逼近
对于为偶数,由约束1, 2, 3, 4可得,有如下形式的多项式结构:
这种结构特点是零极点相互关系固定,当确定了零点位置那么极点位置也就确定了,并且通带和阻带零极点关于对称。
为简便直观起见,这里对进行函数逼近。
绘出得草图,得到:
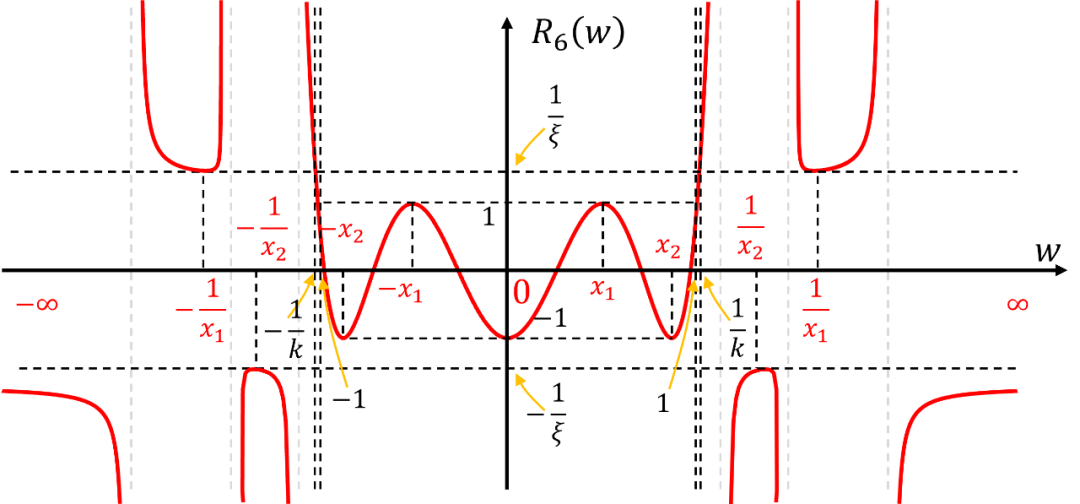
和之前切比雪夫逼近类似,首先建立微分关系,从图中可以观察到对于阶的函数,其通带内极值点在值为1处有个(图中的和),在通带内值为-1处的极值点有个(图中的, 和);在阻带值为处有个(图中的和),在阻带值为处有个(图中的, 和),在阻带的极值点可以通过约束4来推导,个数同通带内极值点。图中所有极值点都用红色字符标注,注意无穷只算一个极值点。对于阶函数,总的极值点有个。函数求导并平方后的极值点个数为。
所有极值点都位于函数值等于和处,另外再除掉频率为和的4个点(图中的和)。
所以最终函数求导后再平方结果如下:
上式为常数,化简得到:
整理得到:
令,再次整理得到最终标准微分方程:
对上式两边积分,得到第一类椭圆积分标准形式,具体求解过程见《滤波器设计中的椭圆函数讲解》,最终得到滤波器特征方程为:
是雅克比椭圆函数,类比于三角余弦函数,可以看到其方程形式和切比雪夫滤波器特征方程(15)一样。
滤波器频率响应:
式中, , 绘图得到:
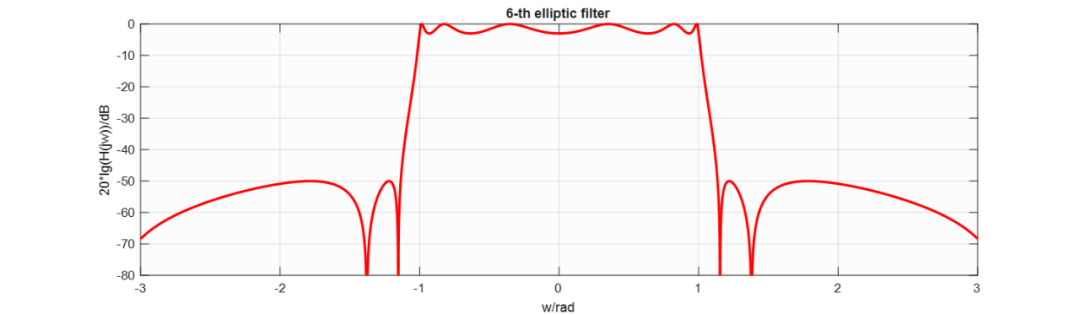
对于其他阶椭圆函数滤波器,令并且,其特征函数标准微分方程为:
上式是一个中间变量,便于分析和后续处理,最终特征函数为:
总结
本章节对巴特沃斯(Butterworth)、切比雪夫(Chebyshev)、椭圆函数(Elliptic Function/Cauer)滤波器综合中的逼近方法进行了讲解,并且做了一些抛砖引玉式的扩展,总体来说函数逼近论比较复杂,比如对切比雪夫滤波器得扩展就在奇数阶设计综合中遇到了困难,这里涉及到比较多的雅可比椭圆函数的知识。后续的其他滤波器综合类文章,都是按照滤波器综合流程来行文,这样更加系统和连贯。
 电子发烧友App
电子发烧友App





















评论