高精度温度测量为工业自动化应用提供基本数据,以确保产品质量和安全。有许多类型的温度传感器可供选择,每种传感器都有其优点和缺点。本应用笔记重点介绍电阻温度检测器(RTD),并阐述了优化测量精度的设计要点。
电阻温度检测器
RTD包含一个元件,其电阻随温度变化。大多数元素是铂、镍或铜。铂RTD提供最佳性能,因为铂在大温度范围内具有最线性和可重复的温度电阻关系。
通常,与热电偶和热敏电阻相比,RTD产生更稳定和可重复的输出。因此,RTD可实现更高的测量精度。
高精度 RTD 测量设计选项
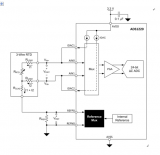
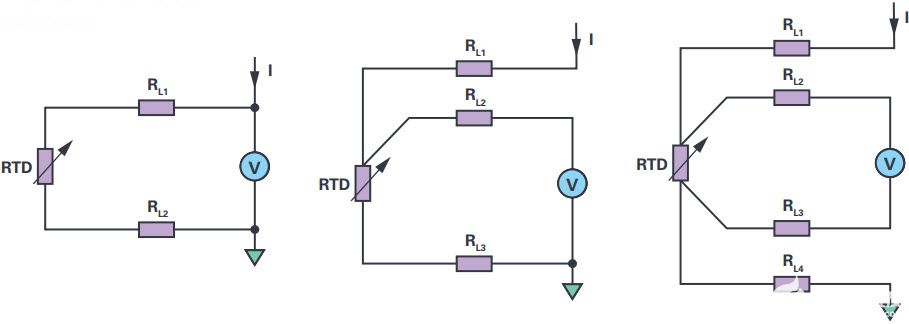
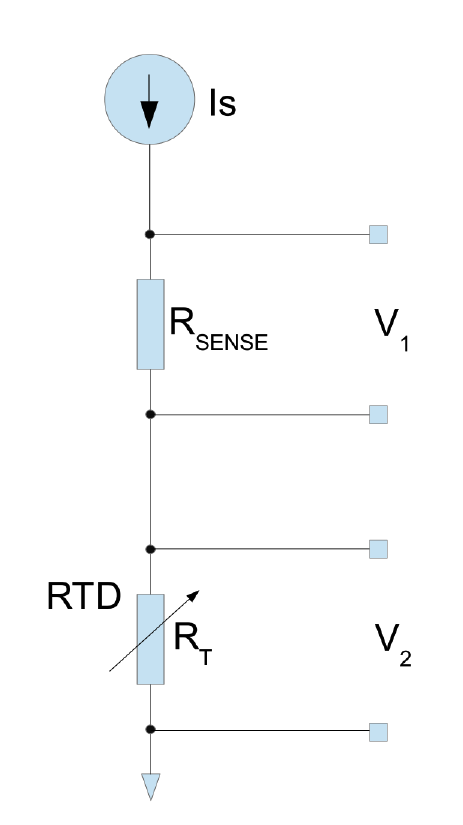
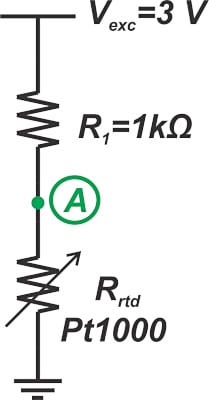
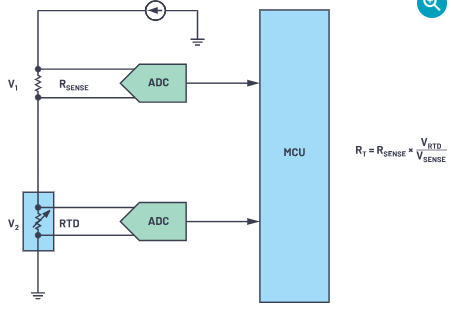
测量RTD的两种最常见方法是恒流激励(图1)和恒压激励(图2)。
目标是精确测量RTD电阻,并使用公式或查找表将其转换为温度。对于理想情况:
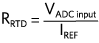
对于恒流励磁,或
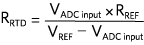
用于恒压励磁。
然而,在实践中,RTD的引线具有电阻。长引线极大地影响了测量精度。因此,图1和图2所示电路测得的实际电阻为:
RTD + (2 × RWIRE),
其中 R线是引线的电阻,假设两根导线具有相同的电阻。虽然理论上可以接受,但相同的 R线意味着两根电线的长度完全相同,并且由完全相同的材料制成。在关键温度检测应用中无法保证这样的假设。因此,RTD 具有 3 线和 4 线配置,有助于消除引线造成的测量误差。
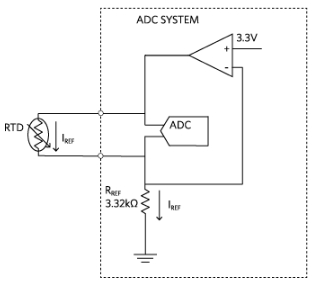
图1.2线恒流励磁配置。
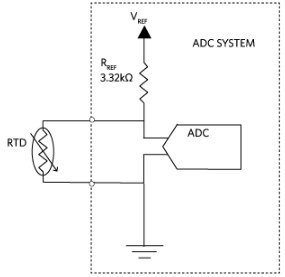
图2.2线恒压励磁配置。
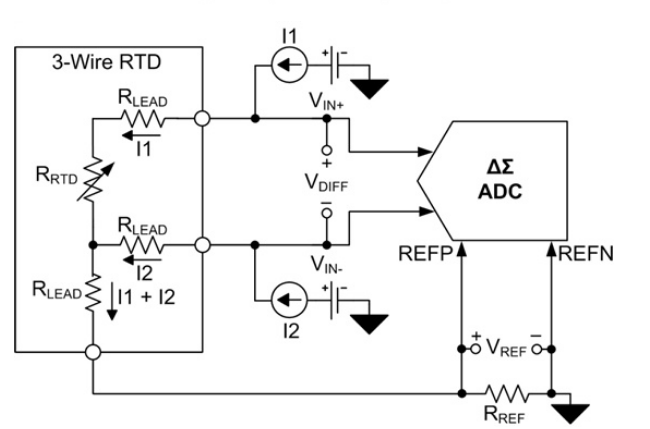
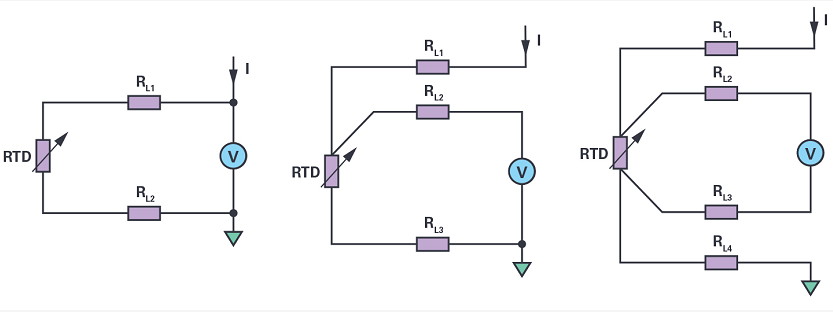
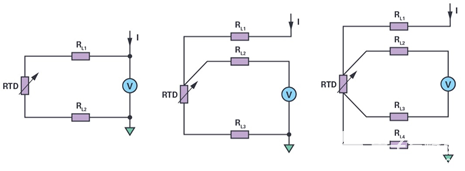
3线RTD配置
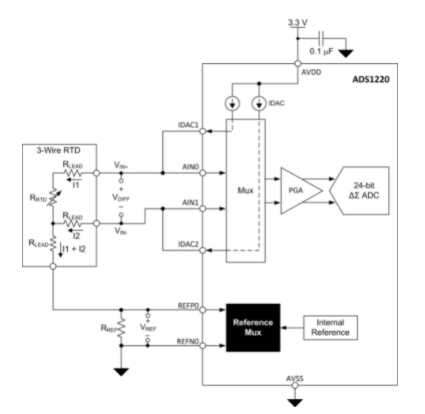
3线RTD的典型恒流和恒压激励电路分别如图3和图4所示。在这两种情况下,ADC都对RTD + R的电阻进行采样线3(其中 R线3是返回引线的电阻)。系统消除了 R线2,因为ADC输入通常是高阻抗的,几乎没有电流流过R线2. 因此,ADC仅测量RTD和R两端的电压线3. R线3 导致测量误差。然而,与2线配置相比,引线贡献的误差减少了约50%。
进一步提高测量精度的一种方法是在电路中添加一个模拟开关。然后,ADC测量电压(VX) 在激励信号的输出端,并得到 R 的值线1. 通过假设 R线1 与 R 大致相同线3、R线3可以减去。参考图3,在电流激励配置中,R线1 电阻等于:

这种提高测量精度的方法确实需要额外的硬件,并增加了软件的复杂性。

图3.3线恒流励磁配置。
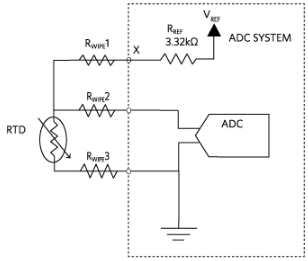
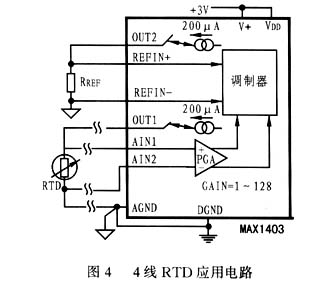
图4.3线恒压励磁配置。
4线RTD配置
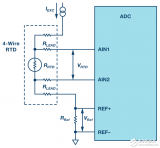
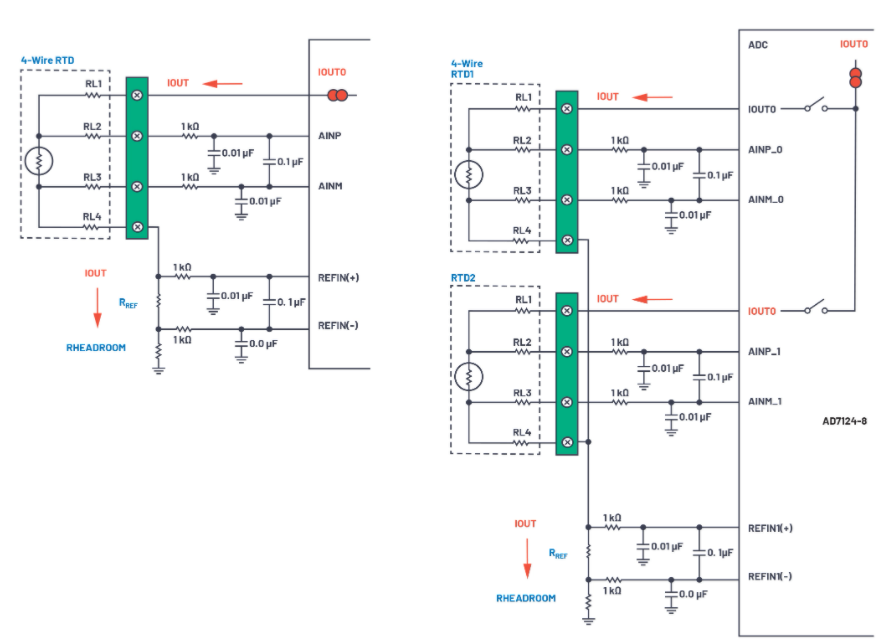
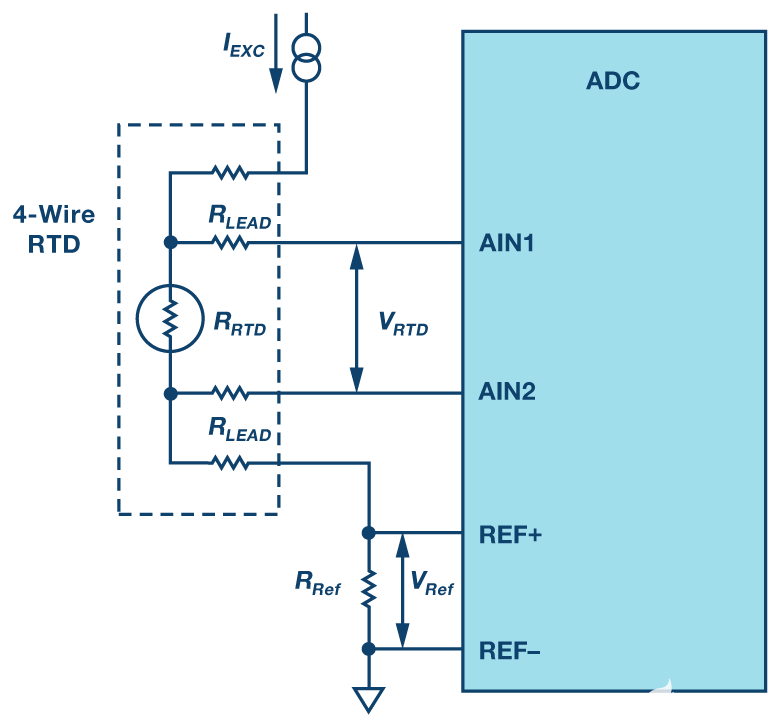
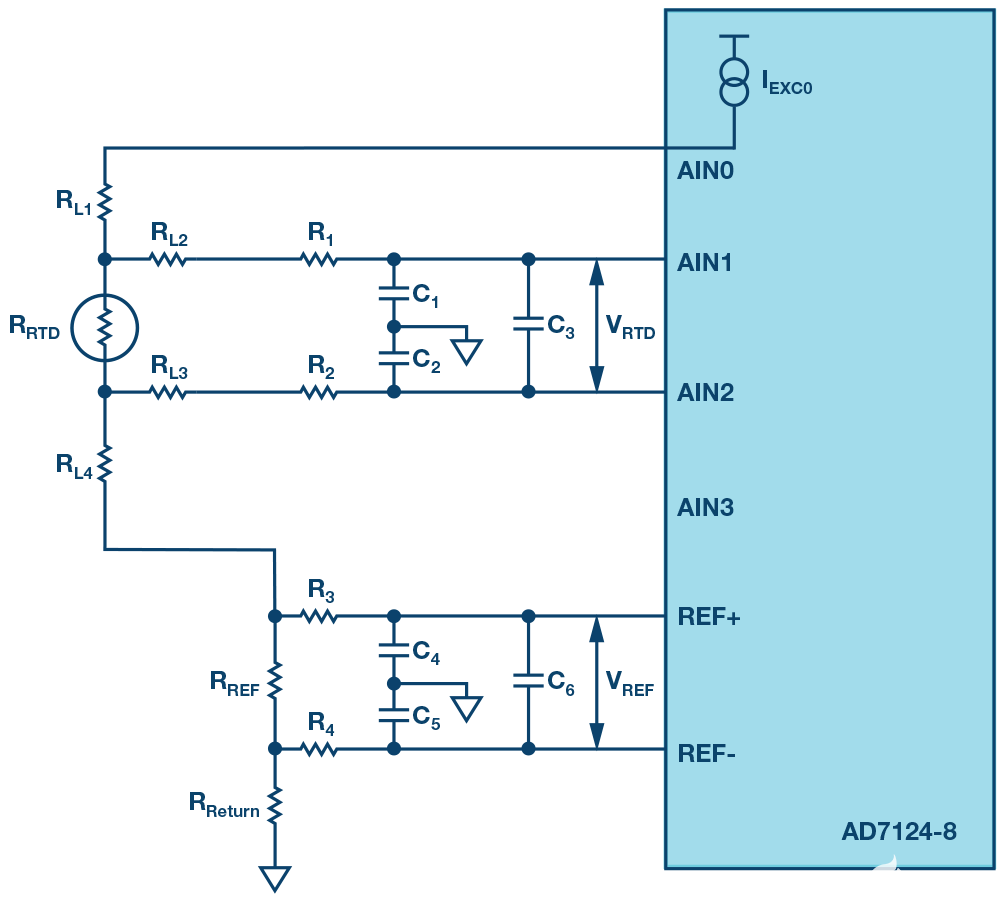
4线RTD配置提供最高的测量精度。图5和图6分别显示了4线RTD的恒流激励和恒压激励电路。对于电流激励配置,
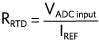
因为没有电流通过R线2 或 R线3.因此,电压过R端线2 + RTD + R线3与RTD两端的电压相同。不幸的是,当使用恒压励磁配置时,由于分压器效应,R线1 和 R线4仍然会在RTD测量中产生误差,除非ADC系统能够测量激励电压输出端的电压(VX).如果电压在 VX已知,则参考电流可以通过下式计算
信号链中的许多其他因素都会影响测量精度。这些因素包括ADC系统的输入阻抗、ADC的分辨率、通过RTD的电流量、基准电压源的稳定性以及激励信号的稳定性。
ADC系统的输入端必须具有高阻抗,以避免引线两端的压降(R线2 和 R线例如 3 线配置)。如果ADC没有高阻抗输入,则应在ADC输入前添加缓冲器。

图5.4线恒流励磁配置。
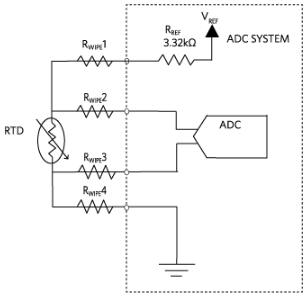
图6.4线恒压励磁配置。
加热误差
虽然RTD是一个传感器,但它也是一个电阻器。当电流通过电阻时,会出现功耗。耗散的功率使电阻升温。这种自热效应会在测量中产生误差。必须仔细选择激励电流,以确保产生的误差在误差预算范围内。计算自热误差的关键公式为
ΔT = (I2REF ×RRTD) × F
其中F是RTD的自热系数,以mW/°C表示。 例如,浸没在冰水中的PT-100铂RTD,自热系数为0.05°C/mW。当测量温度为0°C时,R即热处理等于100Ω。如果 I裁判设置为10mA,自发热误差变为
((0.01A)2× 100Ω) × 50°C/W = 0.5°C。
根据应用程序的不同,此错误可能是可接受的,也可能是不可接受的。对于高精度测量,较低的激励电流可降低自发热误差。例如,如果我裁判降至1mA,自热误差变为0.005°C。 这种程度的错误更容易容忍。虽然降低激励电流可降低自发热误差,但也减小了RTD两端的电压信号范围,因此需要放大RTD信号,以便ADC可以提取更多的离散信号电平。另一种方法是使用更高分辨率的ADC。
到目前为止,所有讨论的公式都涉及 I裁判或 V裁判.但是,如果这些激励信号不稳定怎么办?不稳定可能是由短期或长期漂移引起的。显然,如果激励信号变得不准确,则上述所有计算都有误差。因此,需要定期校准。当然,工程师可以使用具有超低温度漂移和长期漂移的超稳定基准电压源。但是,通常此类设备非常昂贵。或者,比例温度测量方法消除了由不准确的激励信号引起的误差。
比例温度测量
比率测量提供RTD电阻作为参考电阻之比的测量,而不是使用绝对电压测量电阻。换句话说,R即热处理将是 R 的函数裁判而不是 V裁判或我裁判.这使用相同的激励信号来产生RTD两端的电压和ADC的基准电压源。当激励信号发生变化时,该变化会反映在RTD两端的电压和ADC的基准输入上。图7和图8显示了电流激励和电压激励配置的比例测量电路。
一般ADC转换公式为:
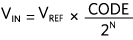
其中
VIN = ADC 输入电压
VREF = 参考电压 (REFP - REFN)
CODE = ADC 代码
N = ADC 的分辨率。
VIN等于RTD两端的电压。对于电流激励模式
VIN = IREF × RRTD 和 VREF = IREF × RREF。
将VIN和VREF代入ADC转换公式可得到,
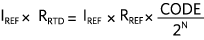
随后,
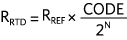
同样,对于电压激励,
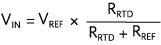
替换 V在进入ADC转换公式产生,
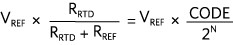
求解 R即热处理给
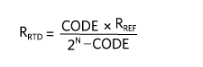
在这两种情况下,简化后,R即热处理成为 R 的函数裁判和 ADC 代码;因此,RTD测量的精度取决于R裁判.因此,在选择基准电阻时,工程师必须选择一个具有低温和长期漂移的基准电阻。
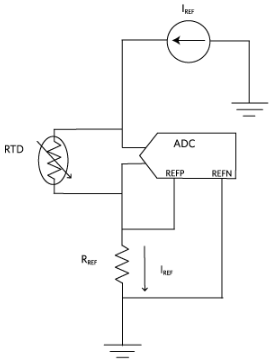
图7.用于比率测量的电流激励配置。
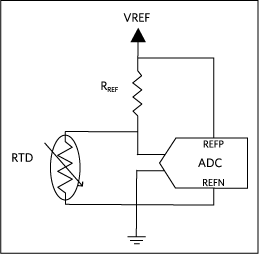
图8.用于比率测量的电压激励配置。
RTD 至温度转换
无论电路对RTD电阻的测量效果如何,如果工程师没有将RTD电阻精确转换为温度的好方法,那么所有的努力都将付诸东流。一种常见的方法是使用查找表。但是,如果分辨率要求高且测量温度范围较宽,则查找表将变得笨拙,并且该方法效果较差。另一种方法是计算温度。
对于铂RTD,Callendar-Van Dusen方程将电阻和温度之间的关系描述为:
R(t) = R0 × (1 + A × t +B × t2+ (t - 100) × C × t3),
其中
R(t) = RTD 电阻
t = 温度
R0 = RTD 在 0°C 时的电阻
A = 3.908 × 10-3
B = -5.775 × 10-7
C = -4.183 × 10-12 当 t < 0°C 时
t > 0°C 时 C = 0
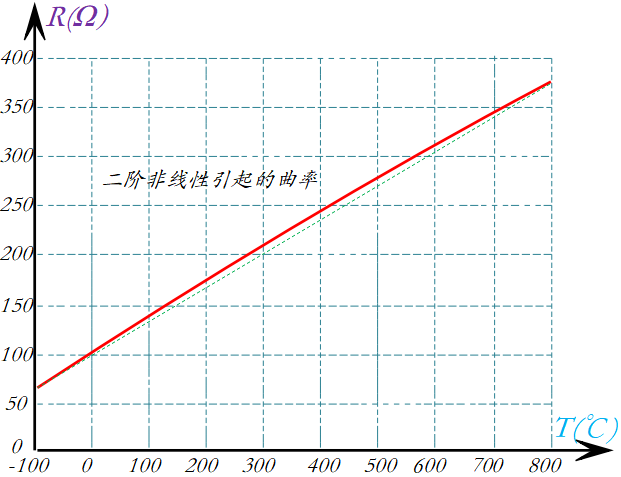
该公式提供了给定已知温度的预期RTD电阻。如果感兴趣的温度范围高于 0°C,则常数 C 变为 0,方程变为二次公式。求解二次方程很简单。但是,如果温度低于0°C并且C常数变为非零,则方程将变为困难的4阶多项式。在这种情况下,多项式插值近似是一个非常有用的工具。这是一个微软Excel解决方案:
在电子表格上,创建两列数据。一列列出温度。第二列列出了根据Callendar-Van Dusen方程计算得出的相应RTD电阻。
创建 X-Y 散点图。
为绘图添加多项式趋势线。多项式的阶数越高,给出的近似值越准确。
在“格式化趋势线”菜单中选择“在图表上显示方程式”。
得到的 PT100 在 t < 0°C 时的多项式方程为:
t = -1.6030e -13 × r6+ 2.0936e -10 × r5-3.6239e -8 × r4-4.2504e -6 × r3+ 2.5646e -3 × r2+ 2.2233 × r -2.4204e2
增加多项式系数的小数位可减少误差。如上式所示,小数点后四位,温度近似误差小于0.005°C,大多数应用都可以容忍。
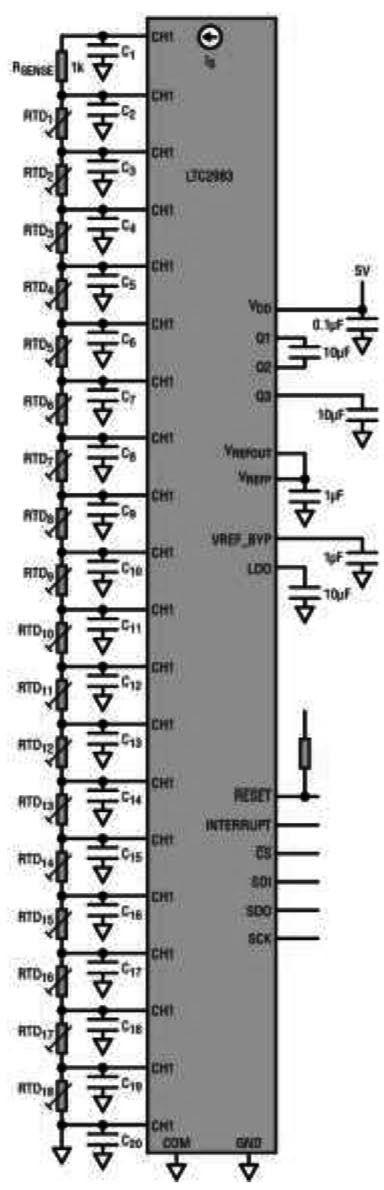
Maxim参考设计解决方案
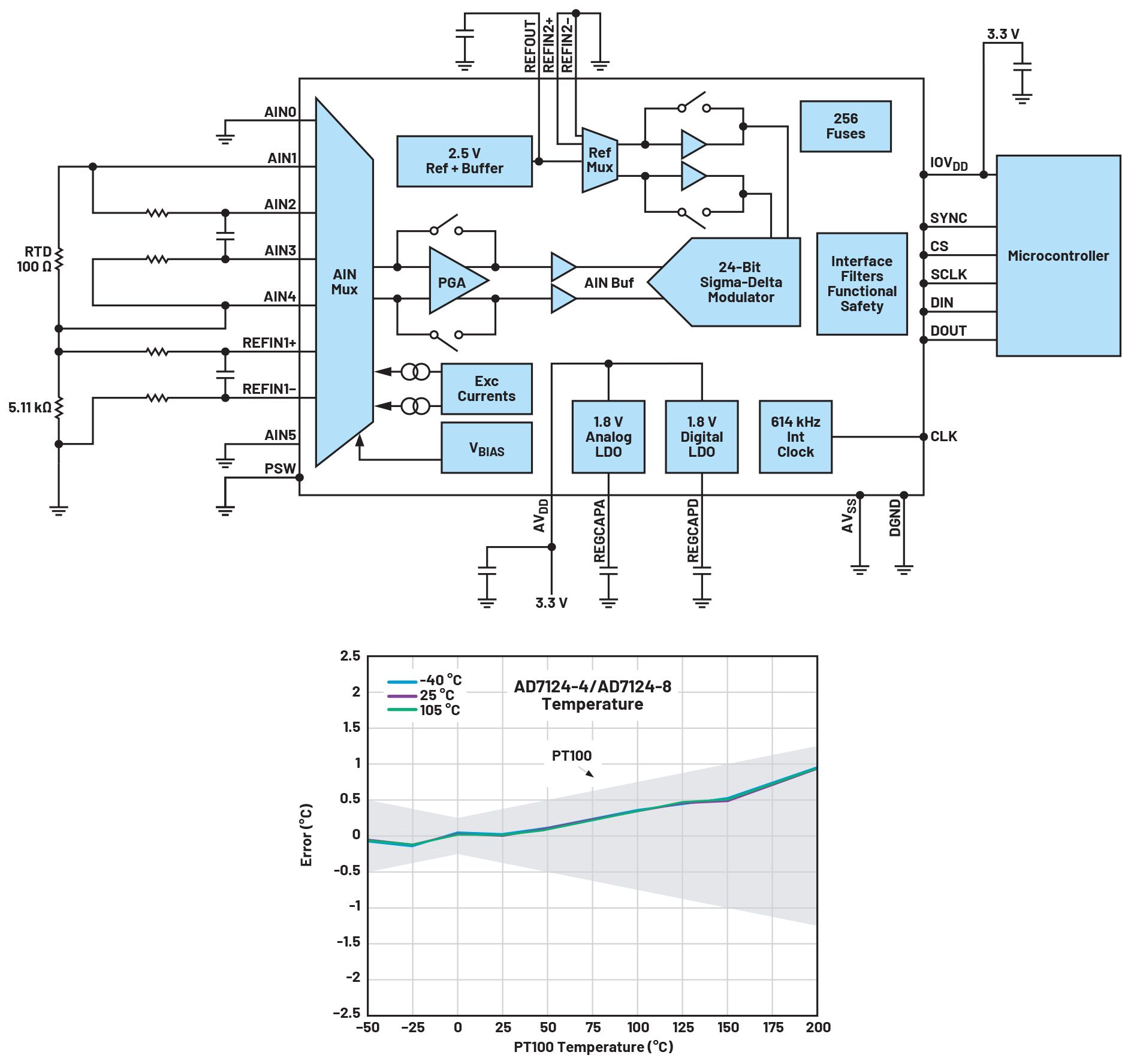
如上所述,MAXREFDES67# 参考设计实现了 4 线比率配置和多项式近似。此外,设计文件和固件可用于后续修改和实施。此外,该参考设计是适用于工业应用的完整通用模拟输入。除了RTD测量外,这种独特的24位前端还接受双极性电压和电流以及热电偶(TC)输入。MAXREFDES67#采用Maxim Integrated的超小型微型PLC外形,在-22°C至3°C范围内具有高达0.1位的有效分辨率,温度误差低至±40.150%。 参考分别是 Omega HH41 温度计、ETI 参考温度计和福禄克 724 温度校准器。将 MAXREFDES67# 连接的 RTD 探头(Omega P-M-1/10-1/4-6-0-G-3)放置在福禄克 7341 校准槽中,并在 20°C 下进行校准。
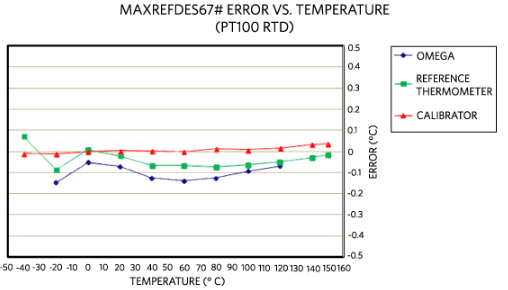
图 12.MAXREFDES67# 误差与温度的关系,使用 Omega P-M-1/10-1/4-6-0-G-3,4 线 RTD,在 20°C 下校准。
结论
温度是测量最多的工业参数。虽然使用比率法和多项式近似等技术的精密系统设计可以制造出非常精确的测量系统,但借助Maxim的参考设计系统,设计人员现在可以比以往更快地开发高精度RTD温度测量或热电偶测量系统。MAXREFDES67#允许修改和实现,是工业应用的完整通用模拟输入。除RTD测量外,它还接受双极性电压、电流和热电偶输入,具有有效的分辨率和低测量误差,使其比其他选项更有效。
审核编辑:郭婷
 电子发烧友App
电子发烧友App











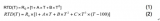

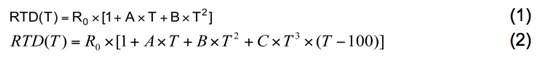
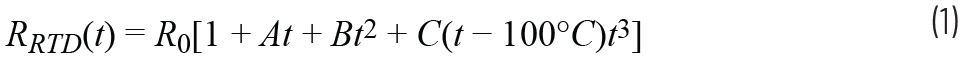

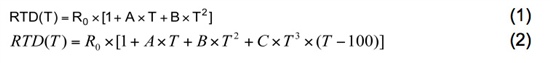
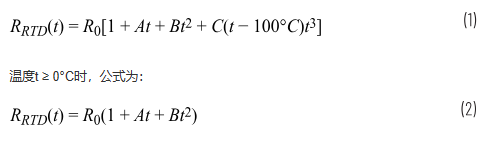











评论