应用推挽式功率放大电路的匹配电路设计

介绍了一种分析同轴线变换器的新方法，建立了理想与通用模型，降低了分析难度和简化了分析过程。通过研究分析，提出了一种同轴变换器与集总元件相结合的匹配电路设计方法，通过优化同轴线和集总元件的参数，实现放大器的最佳性能。利用该方法设计了一款应用于推挽式功率放大电路的匹配电路，仿真结果表明，匹配效率高达99.93%。

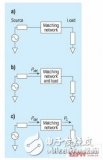
阻抗变换器和阻抗匹配网络已经成为射频电路以及最大功率传输系统中的基本部件。为了使宽带射频功率放大器的输入、输出达到最佳的功率匹配，匹配电路的设计成为射频功率放大器的重要任务。要实现宽带内的最大功率传输，匹配电路设计非常困难。本文设计的同轴变换器电路就能实现高效率的电路匹配。同轴变换器具有功率容量大、频带宽和屏蔽好的特性，广泛应用于VHF/UHF波段。常见的同轴变换器有1:4和1:9阻抗变换，如图1所示。但是实际应用中，线阻抗与负载不匹配时，它们的阻抗变换不再简单看作1:4或1:9.本文通过建立模型，提出一种简化分析方法。

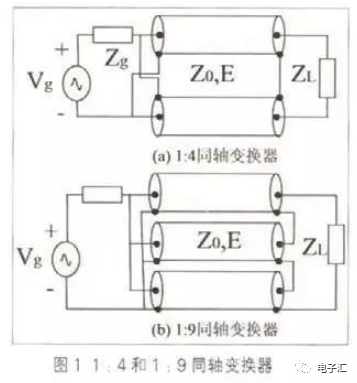
1 同轴变换器模型

同轴变换器有三个重要参数：阻抗变换比、特征阻抗和电长度。这里用电长度是为了分析方便。当同轴线的介质和长度一定时，电长度就是频率的函数，可以不必考虑频率。

1.1理想模型

理想的1:4变换器的输入、输出阻抗都匹配，每根同轴线的输入、输出阻抗等于其特征阻抗Z0,其等效模型如图2所示。

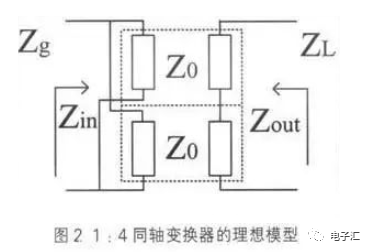
其源阻抗Zg与ZL负载阻抗变换比为：

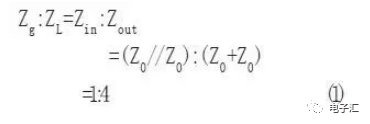
图2和公式（1）表明：变换器的阻抗变换比等于输入阻抗与输出阻抗之比。

同轴变换器的输入阻抗等于同轴线的输入阻抗并联，输出阻抗等于同轴线的输出阻抗串联。

1.2通用模型

由于特征阻抗是实数，而源阻抗与负载阻抗一般都是复数，所以，就不能简单的用变换比来计算。阻抗匹配就是输入阻抗等于源阻抗的共轭，实现功率的最大传输。特征阻抗为Z0,电长度为E的无耗同轴线接复阻抗的电路如图3所示。

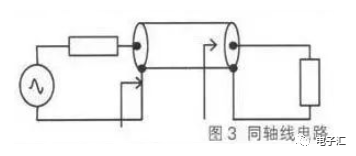
由于源阻抗与同轴线特征不匹配，电路的反射系数就不是负载反射系数。

由于同轴线是无耗的，进入同轴线的功率就等于负载消耗的功率。那就可以把电路简化只有一个负载Zin,又因为Zg与Zin都是复数且串联，就可以把Zg中的虚部等效到Zin中，最后得到反射系数为：
 

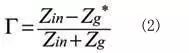
其中：

当反射系数为零时，功率可以无反射的传输，这时阻抗实现完全匹配。

由公式（2），反射系数为零可以等效为分子为零，即：

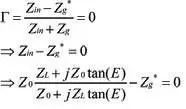
其中：
 

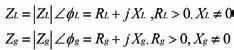
当E为90o时，可得：

由于特征阻抗为实数，ZLZg*为实数时，方程才有解或才能完全匹配。当ZL和Zg为实数时，就是常用的λ/4阻抗变换。

当E不等于900,利用实部与虚部都等于零得方程组：

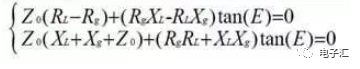
整理化简得：

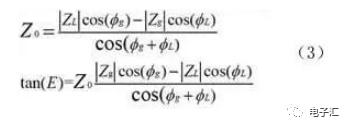
公式（3）说明，不是任意两个复阻抗都可以完全匹配，必须满足特征阻抗为正实数；可以并联或串联电抗元件，使两个不可能完全匹配的复阻抗完全匹配。

通用模型是结合理想模型和同轴线分析建立，如图4所示。把1:N同轴变换器等效一根同轴线，利用同轴线的分析结果，更容易获得特征阻抗和电长度参数。

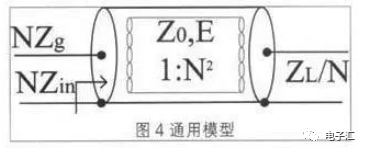
特别对于利用同轴变换器设计的匹配电路，可以简化设计步骤，减少工作量。

2 宽带匹配电路的设计

通过对同轴变换器的分析，可以通过调谐特征阻抗和电长度完成阻抗匹配。

但是实际同轴线的特征阻抗是有一定规格的，不是任意的，而且电长度又是随频率变化的，所以采用同轴变换器和集总元件联合实现宽带匹配的方式。

2.1.集总元件匹配电路

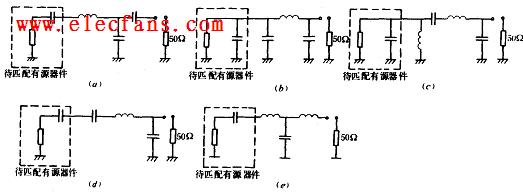
复阻抗可以用电阻与电抗串联表示，也可以用电阻与电抗并联表示，这两种表示的等效电路如图5所示。

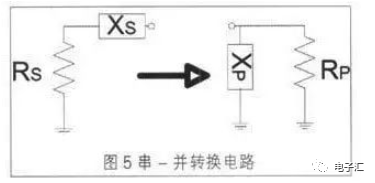
它们都是指同一个复数，其转换关系为：

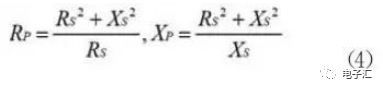
公式4表明，电阻并联电抗可以减小其复阻抗的实部，再串联电抗抵消其虚部，就可以实现Rp到RS阻抗匹配。所需的电抗值可以通过表达式4计算，且Xp与XS取不同性质的元件，如果Xp用电容，XS就用电感。

集总元件实现阻抗匹配原理：电阻并联电抗减小其实部，再串联电抗抵消其虚部，达到两个纯电路的匹配；当匹配的不是纯电阻时，可以采用抵消和吸纳虚部的方法实现复阻抗的匹配。

2.2联合匹配电路

以Freescale公司MRF6VP2600推挽式MOSFET管的匹配电路设计为例，首先确定匹配电路的基本结构和同轴变换器的阻抗变换，然后再确定特征阻抗、电长度和集总参数。由于输入匹配电路设计与输出匹配电路类似，下面详细研究输出匹配电路设计。MRF6VP2600的DATASHEET给的源极-源极的输出阻抗如图6所示。

图6 MRF6VP2600的输入-输出阻抗

输出匹配电路中，由于功率管采用推挽式工作，所以在输出端加入1:1巴伦实现不平衡-平衡变换。利用通用模型，下面的工作就简化为同轴线与集总参数的匹配电路设计。同轴线的特征阻抗和电长度计算公式为：

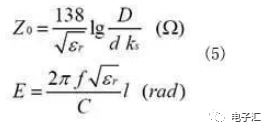
式中，Er为内部填充介质的相对介电常数；D为外导体内径；d是内导体外径；为内导体系数，单股内导体时为1;C为空气中光的速度；f为工作频率，L为同轴线的长度。

公式5表明，电长度与频率呈线性关系，且其长度越短，电长度受频率的影响越小。

2.3仿真验证

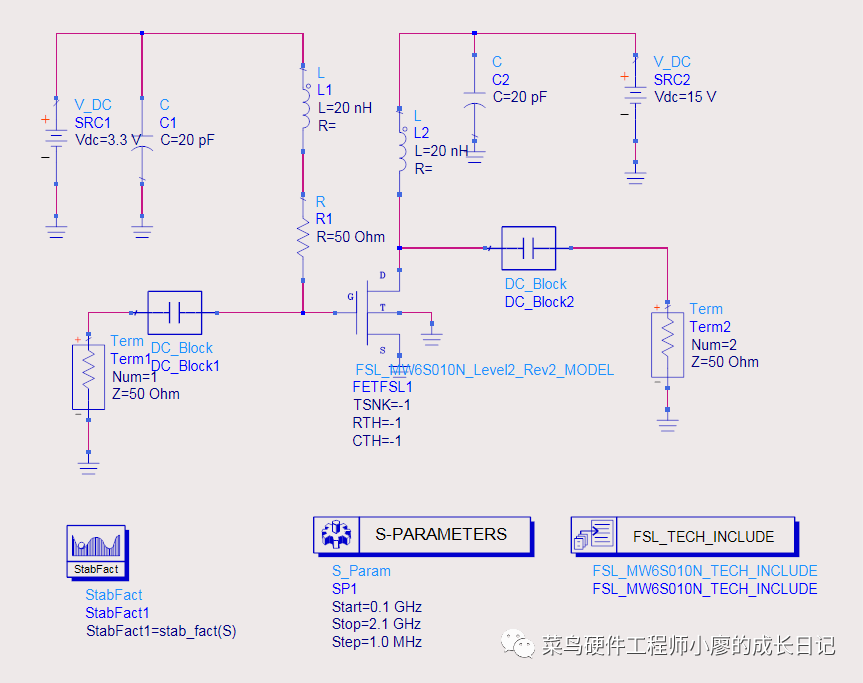
利用安捷伦公司的ADS工具进行输出匹配电路设计与仿真，一般可采用大信号S参数仿真和谐波仿真，由于本文设计用于推挽式工作的匹配电路，所以选用更直观的谐波平衡仿真。利用同轴线和巴伦的模型进行仿真的电路如图7所示。

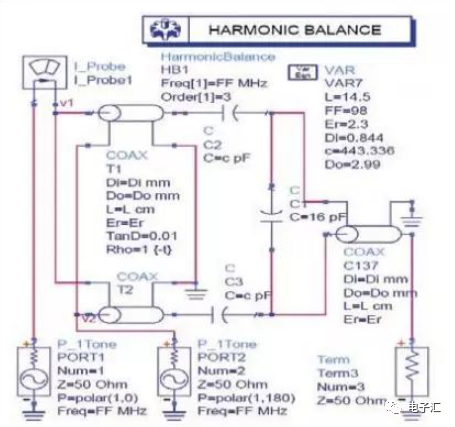
图7 仿真原理图

由于图7的负载阻抗的实部是随频率增减而减少，所以在同轴变换器的两端并联电容。可以很容易对电路进行手动调谐和自动优化，最后的仿真结果如图8所示。

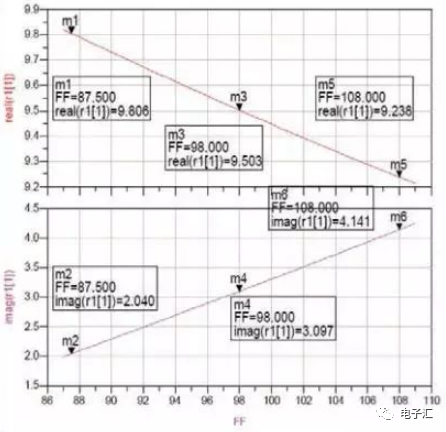
图8 （87.5-108）Mhz匹配阻抗

由图6,图8可以得到各频点的反射系数；再根据反射系数与频率的关系，可以求得匹配电路在工作频带的反射系数；最后根据匹配效率与反射系数的关系，求得匹配电路的匹配效率。具体结果见表1。

表1 反射系数与匹配效率的计算结果

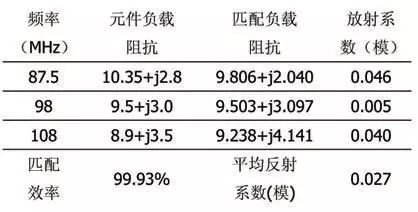
从表1可以得到，匹配电路的在工作频段内匹配效率达99.93%,实现了较好的匹配。

3总结

本文建立同轴变换器的理想模型和通用模型，提出一种新颖的和简单的分析方法。通过分析，同轴线的特征阻抗和电长度对匹配电路的性能有很大影响。设计了一款推挽式MOSFET管的输出匹配电路，仿真结果表明：匹配效率达99.93%.

编辑：黄飞