作为模拟工程师,环路稳定性是一个绕不开的话题,很多运算放大器的书籍也或多或少对运算放大器的稳定性都有介绍,但看下来都不够完整,或者部分知识点有些陈旧,基于此,搬运工重新梳理并整理成本文运算放大器的稳定性。本文比较长,为了更有目的性的阅读,大家可以带着以下几个问题点去详细阅读本文,并在阅读完之后再回头来看看这些问题是否都得到了很好的答案。
1. 运算放大器的开环增益、环路增益、闭环增益的区别?
2. 运算放大器环路不稳定的判定条件以及原因?
3. 运算放大器环路稳定性的判定依据?
4. 什么是相位裕度和增益裕度?
5. 如何理解波特图中的幅度改变率、相位改变率、极点、零点?
5. 如何理解运算放大器规格书中Gain/Phase频率曲线中Phase有正有负?
6. 如何根据规格书中开环Gain/Phase频率曲线快速判定环路稳定性?
7. 如何理解相位频率曲线的非单调性以及其对群延时的影响?
8. 如何理解环路增益AOLβ中开环增益AOL和反馈系数β随频率变化的特性?
一、运算放大器的负反馈
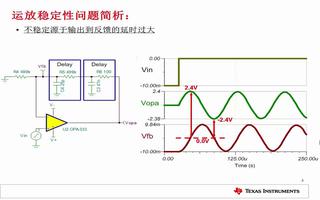
负反馈电路在运算放大器的应用中起着非常重要的作用,它可以改善运放的许多特性,比如稳定增益,减小失真,扩展频带,阻抗变换等。但负反馈的引入也有可能会使得运算放大器电路不稳定,轻则带来时域上的过冲,重则会引起自激振荡。运算放大器的自激震荡
二、运算放大器的稳定性
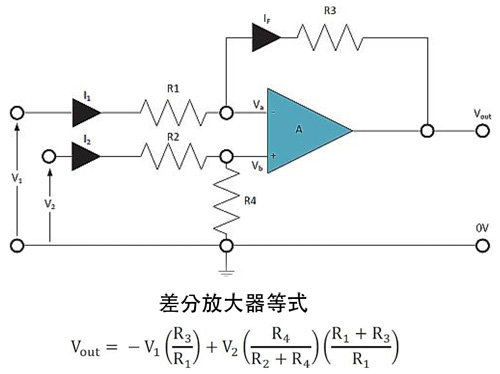
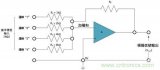
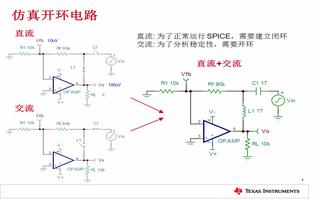
为了简化分析,下面以同相放大器为例,来从零开始解析运算放大器的稳定性,如下图所示,是同相放大器的环路系统框图以及对于同相比例放大器的实际电路示意(标注出对应的反馈系数-β网络)。
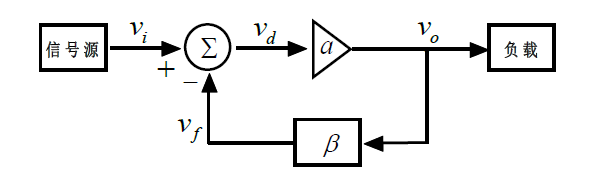
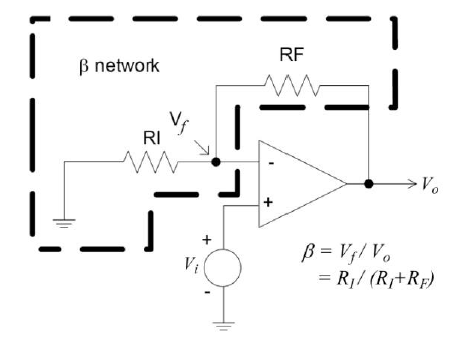
从上图反馈环路系统框图中,得知对于一个负反馈电路,主要包含:
增益模块:增益为a,接受输入差分信号vd,输出vo,即vo=a×vd,这里对于同相比例放大电路,其增益模块即是运算放大器本身,a则是其开环增益AOL。
反馈网络:反馈信号网络,vf=β×vo,β则是该反馈网络的增益,也是常说的反馈系数。
叠加模块:vd=vi-vf,这里可以看到所谓负反馈,是在输入信号源上减去反馈的信号后得到差分信号,如果是vd=vi+vf,则是正反馈系统。 基于以上的简单推导,可以得到同相比例放大电路的闭环增益(Acl)表达式如下:
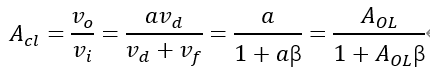
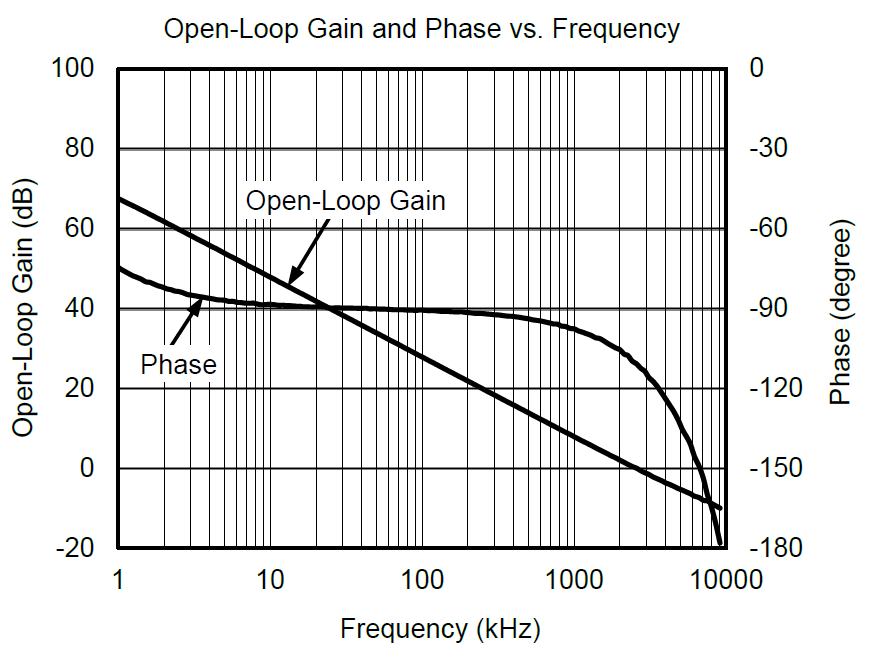
AOLβ,这是一个非常重要的表达式,称之为环路增益,从上述闭环增益的表达式可以看出,一个负反馈系统的稳定性程度主要取决于其环路增益AOLβ,这里β对于同相比例放大电路,因为反馈网络只有电阻元件,其值跟频率没有关系,β=vf/vo=RI/(RF+RI),而AOL则是一个随频率变化的曲线(如上图OPA规格书中给出的开环增益和相位与频率的曲线图,其幅度和相角都会随频率变化而变化 ),所以从数学上理解,AOL是一个复数,会对应有幅度和相角度,所以这里对于环路增益AOLβ又可以表达成如下形式(其中f是代表频率,θ代表相角):
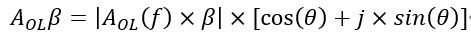
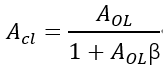
所以当AOLβ=-1的时候,1+AOLβ为无穷大,闭环增益趋于无穷大,这个时候输入端任何轻微的扰动都会在输出引起剧烈的反应,此时负反馈系统变成了正反馈,进而导致运算放大器的自激震荡的产生。从AOLβ的复数表达式来看(这里是以往所有讲运算放大器稳定性都没有提到的一个概念),对于|AOLβ|=1,当θ=-180°时,cos(θ)=-1,sin(θ)=0,则有AOLβ=-1,所以对于不稳定的条件是|AOLβ|=1以及θ=-180°。所以判定稳定性时,需要保证远离以上两个进入不稳定的条件,下面分开从这两个不稳定条件来看:
1. 当AOLβ的相角θ=-180°时(信号过系统之后的相移为-180°,负反馈变成正反馈):|AOLβ|<1:0<1+ AOLβ<1,正反馈信号逐渐衰减,会产生过冲但不会震荡。|AOLβ|≥1:AOLβ=-|AOLβ|≤-1,即1+ AOLβ≤0,如果1+ AOLβ<0,则Acl<0,但因为运算放大器本身的限制,对于同相比例放大无法产生负的闭环增益,从而最终只能工作在1+ AOLβ=0的状态,导致运算放大器工作在不稳定条件下而发生震荡。因此在|AOLβ|≥1的任何时候都需要避免反馈环路的相移达到或超过180°。
2. 当|AOLβ|=1时:θ<-180°,这里主要看相位余量的大小,会有过冲,但不会震荡,通常所说的相位裕度,就是指在|AOLβ|=1(环路增益20lg(1)=0dB)时候的相移距离-180°差值,一般AOLβ至少有45°的相位余量才能让负反馈系统足够稳定。θ≥-180°,会震荡。这里先不展开分析,为了更形象的说明上面两个判定环路稳定性的依据,我们有必要先引入一个分析环路稳定性的必备工具,波特图。
三、环路稳定性少不了的工具-波特图
这里先简单回顾下波特图的几个基本概念:
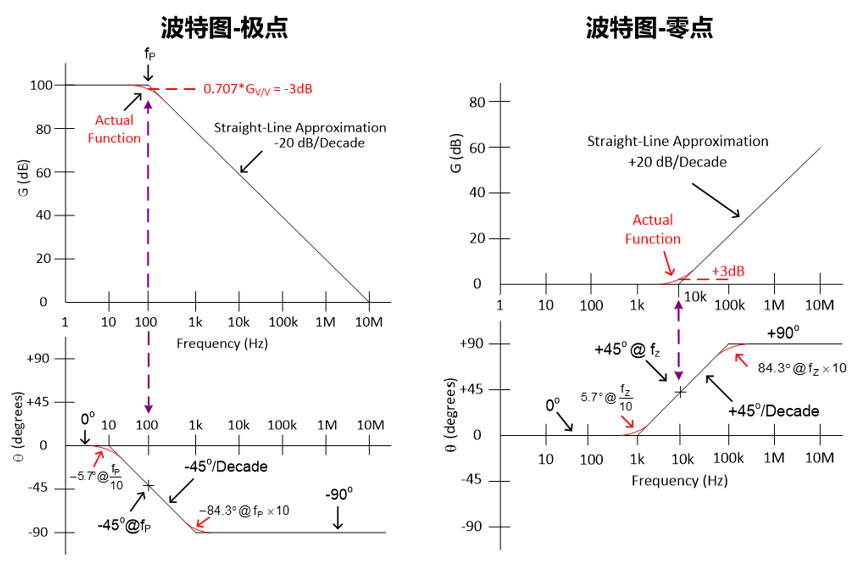
1. 幅度改变率(Roll off Rate):幅度曲线中幅度改变的速率,一般用 dB/decade为单位。为正(+)值时表示上升,为负(一)时表示下降。
2. 相位改变率:相位曲线中相位改变的速率,一般用°/decade 为单位。为正(+)值时表示上升,为负(一)时表示下降。
3. Decade: 十倍频,频率按 ×10 的速度增加,如 10KHz 到 100KHz 为一个 Decade。常与其他单位配合用来表示某个量在 10 倍频程中改变的大小。
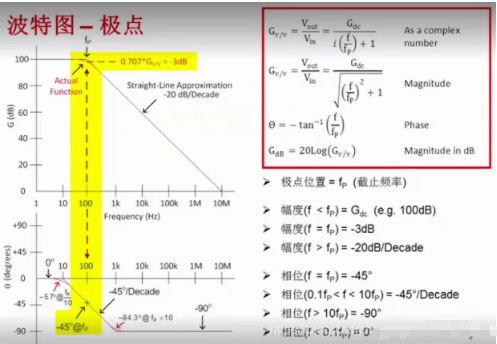
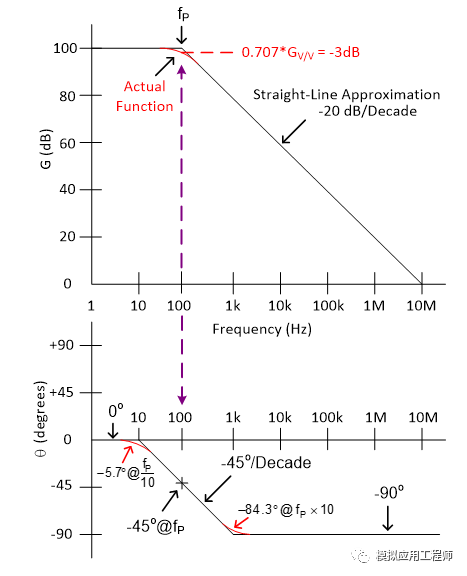
4. 极点:传递函数分母上的转折点称为极点。以上图为例,单个极点响应在波特图(幅度或增益曲线)上具有按 一20dB/decade 斜率下降的特点。与图中的理想曲线不一样的是,在现实中,极点位置在增益等干直流增益减去 3dB 的地方,该外对应的频率即为转折频率。在相位曲线上,极点在转折频率上具有-45°的相移。相位在转折频率的两边以-45°/decade 的斜率变化为 0°和-90°。请注意极点是如何影响直到高于和低于极点频率 10倍频程处的相移的。单极点电路可以用简单的 RC 低通滤波器表示。
5. 零点:和极点对应,传递函数分子上的转折点称为零点。以上图右图为例,单个零点响应在波特图(幅度或增益曲线)上具有按 +20dB/decade斜率上升的特点。与图中的理想曲线不一样的是,在现实中,零点位置在增益等于直流增益加上3dB的地方,该处对应的频率即为转折频率。在相位曲线上,极点在转折频率上具有-45°的相移,相位在转折频率的两边以 +45°/decade 的斜率变化为 0°和 +90°。请注意零点是如何影响直到高于和低于零点频率 10 倍频程处的相移的。单零点电路可以用简单的 RC 高通滤波器表示。到这里为止,回顾了波特图中的几个重要概念,下面我们来看看如何用波特图来帮助我们分析运算放大器的稳定性。
四、利用波特图分析运算放大器环路稳定性
相位裕度定义:在运放开环增益和开环相移图中,当运放的开环增益下降到1(0dB)时,开环相移值减去-180°得到的数值。
增益裕度定义:在运放开环增益和开环相移图中,当运放的开环相移下降到-180°时,增益dB值取负,或者是增益值的倒数。
从相位裕度和增益裕度的定义(上述定义摘录《你好,放大器》2.14),可以简单的认为相位裕度和增益裕度越大,说明放大器越容易稳定,但显然仅仅用相位裕度和增益裕度这两个指标来判定环路稳定性是不够的,上面我们有讲过判定运算放大器环路稳定性的两个依据(从工程经验上来看,第二个判定依据实际应用中更好去衡量):
1. 当AOLβ的相角θ=-180°时|AOLβ|<1:会产生过冲但不会震荡。|AOLβ|≥1:会震荡。
2. 当|AOLβ|=1时:θ<-180°,会有过冲,但不会震荡,相位余量45°以上环路更稳定。θ≥-180°,会震荡。
可以看到,对于运算放大器的环路稳定性的判定,本质上都是对环路增益AOLβ的判定,所以严格来讲,上述对相位裕度和增益裕度的定义并不准确,应该增加一个条件,即对于单位增益的时候,β=1,这个时候环路增益AOLβ就是运算放大器的开环增益。因为相位裕度和增益裕度是用来衡量运算放大器稳定性比较量化的指标,所以我们修正下这两个定义如下:
相位裕度定义:在环路增益和相移频率曲线中,当环路增益下降到1(0dB)时,相移值减去-180°得到的数值。
增益裕度定义:在环路增益和相移图中,当环路相移下降到-180°时,增益dB值取负,或者是增益值的倒数。
基于此,我们来参考TI的OPA2991规格书中关于相位裕度(Phase Margin)这个指标的标注,可以看到,实际对于器件来说,相位裕度都是对于给定闭环增益(G=+1)条件下的一个指标,即β=1,AOLβ=AOL。

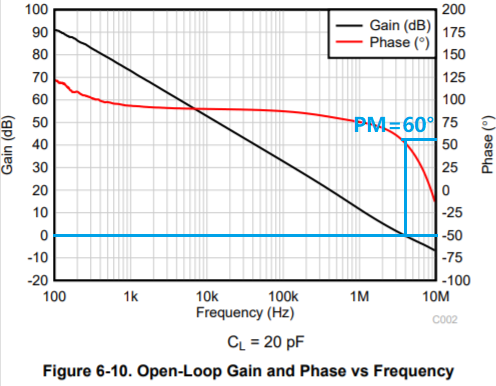
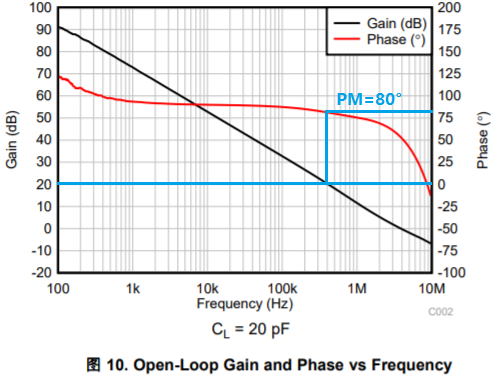
上图是OPA2991规格书中Open-Loop Gain and Phase频率响应曲线,基于这个曲线,对于G=+1(β=1)的时候,从图中读出在0dB处,其相位裕度为60°,可以判定OPA2991在单位增益(跟随器)时环路是稳定的。
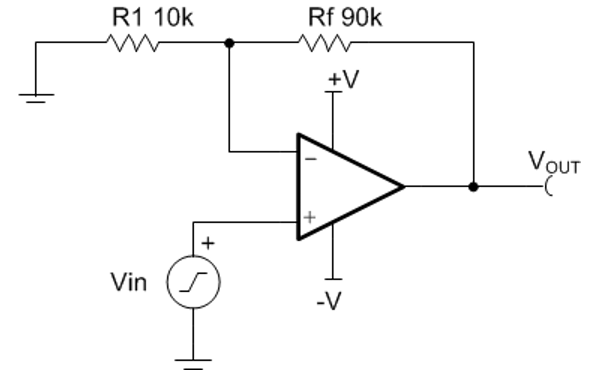
上面讨论的都是单位增益,如下图所示,是一个典型的同相10倍放大电路,该电路的反馈系数β=R1/(R1+Rf)=1/10,1/β=20log(10)=20dB。
对于环路增益AOLβ取对数计算,可以得到如下:
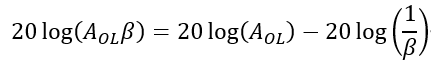
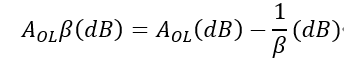
所以对于环路增益AOLβ=0dB处的相位裕度,即可以在OPA2991开环增益曲线上先画出1/β(20dB)的线,然后AOL和1/β曲线交叉处即是环路增益AOLβ=0dB处,同时其对应的Phase就是AOLβ=0dB处的相位裕度80°(这里主要是因为对于纯电阻的反馈网络β是不会引起额外的相频曲线的变化),所以对于OPA2991在G=+10的条件下,根据其环路增益的相位裕度为80°,判定环路稳定的。
五、环路稳定性分析中常见的几个疑惑
1. 运算放大器规格书中开环增益曲线中的Phase有正有负。

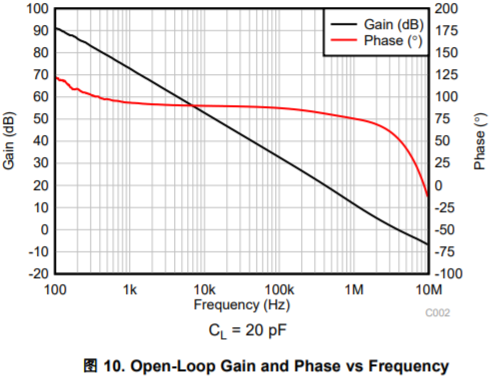
有细心的同学可能已经注意到,本文上述提到过的两个开环增益/相位频率曲线中Phase的数值不太一样,上图(左)的Phase都是负值,上图(右)的Phase则是从正到负。这里我们要先明确一点,对于信号经过运算放大器,其相位肯定是滞后的,即相角是负的。
对于上图(左)中标注的Phase就是我们正常理解的相移,对于这种图示,其相位裕度是读出来的Phase-(-180°)。
对于上图(右)中标注的Phase,其实是Phase Margin,即Phase+180°的值。
2. 为什么有些运放规格书中相位频率曲线不单调?不单调会带来什么影响?一般运算放大器规格书中都会标注G=+1时候的相位裕度,通常对于单极点运算放大器来说,其相位随频率变化是单调的,单位增益处的相位裕度是最小的,只要保证了单位增益处的相位裕度满足稳定性判定依据即可,上述提到的两种开环增益/相位频率曲线均符合。但这并不是绝对的,如下是国内运算放大器厂商思瑞浦TPA5562数据手册中的开环增益/相位频率曲线。
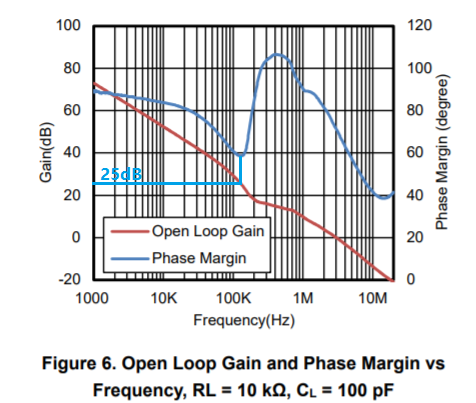
从上图可以看到,TPA5562在单位增益(0dB)处的相位裕度是70°,但在25dB处的相位裕度是60°(25dB处的相位裕度比0dB处要小),其整个相位频率曲线是非单调的,可以明显看出,在120kHz频率处,TPA5562内部做了零点补偿,从而使得相位以+45°/decade的速率上升。单纯的从环路稳定性来看,TPA5562在1/β>0dB以上的环路增益对应的相位裕度都可以满足PM>60°,即保证了环路稳定性,但这种相频曲线对实际应用会产生什么影响呢?这里引入群延时(Group Delay)的概念,输出正弦波和输入正弦波之间,会存在相移,也就相应的存在延时,当输入波形为复合波形,包含多个不同频率的正弦波,且它们的相移没有特殊的规律,就可能出现不同的延时,这会引起输出波形与输入波形形态不同,造成线性失真。所以对于TPA5562这种相频曲线,对于输入信号是包含100kHz~400kHz之间的多个不同频率正弦波的复合波形,则输出虽然环路稳定,但会造成严重的线性失真。(本文主要讲环路稳定性,这里简单借助群延时的概念说明下这种相频曲线的实际应用影响,后续可以单独详细讨论群延时。)
3. 反馈系数β会随频率变化么?
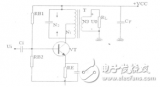
上面讨论的都是基于反馈网络是纯电阻,即反馈系数β是不随频率变化的值,然后对于实际应用中很多时候反馈网络包含了电容,对于包含电容的反馈网络的反馈系数β的表达式就是一个随频率变化的函数。
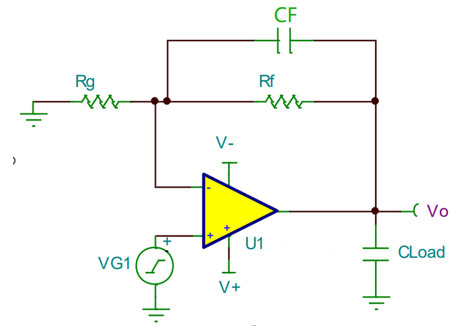
如上图所示,是一个典型的在比例放大电路上增加了反馈电容的电路,这个时候其β的表达式如下,其是一个随频率变化的值,这个时候分析环路稳定性需要考虑1/β引入的额外的零极点(这部分后续会单独写文章讨论关于同相比例放大电路的CF补偿电容的计算)。
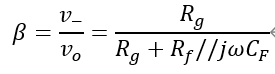
 电子发烧友App
电子发烧友App













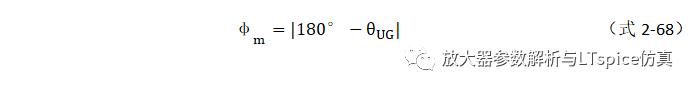










评论