为确保系统满足所需的精度规范,透彻了解不同的误差源非常重要。决定信号链精度的最关键要素之一是A/D 转换器 (ADC),这是本文的重点。请记住,ADC 的精度可以用绝对精度、相对精度和总未调整误差 (TUE)来表征。
一个偶尔让年轻工程师感到困惑的常见问题是:精度与分辨率有何关系?例如,我的 12 位 ADC 是否也是 12 位精度的?
ADC 设计参数——分辨率
分辨率指定了 ADC 特性曲线中的步数(step)。对于具有统一步长的理想 ADC,分辨率决定了模拟输入电压的最小变化,使输出变化一个计数。例如,具有 12 位分辨率的 ADC 可以解析 2^12中的 1 部分(part)(4096 中的 1 部分)。换句话说,12 位 ADC 可以检测小至满量程值的 0.0244% 的电压。然而,这并不意味着转换误差(ADC 输出的输入和模拟等效值之间的差异)小于 0.0244%。
分辨率主要是一个设计参数,而不是性能规格。它没有指定实际由非理想效应(如 ADC 非线性、偏移和增益误差)决定的转换误差。
ADC 精度:当精度低于分辨率时
在数据转换器中,通常用位数来表示精度。例如,我们可以说这个 ADC 是 12 位精度的。这意味着转换误差小于满量程值除以 2^12。换句话说,转换误差小于一个 LSB(最低有效位)。
考虑到这一点,这可能不是表达性能准确性的准确方法,因为不清楚该特征中实际包含哪些误差源。然而,它似乎通常指的是偏移、增益和积分非线性 (INL) 误差的综合影响。转换器的精度可能远低于其分辨率。
例如,考虑下面图 1 中所示的 12 位 ADC。
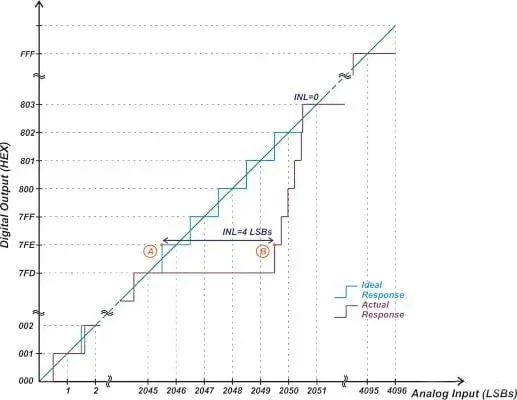
(12 位 ADC 示例)
图中,蓝色和紫色曲线分别是理想特性曲线和实际特性曲线。在这个特定的例子中,偏移和增益误差被校准掉了。代码 7FD 的宽度为 5 个 LSB,这导致代码 7FE 处出现 4 个 LSB 的 INL 错误。此代码中的错误由以下原因给出:

由于转换误差等于满量程值除以 2^10,我们称其精度为 10 位。上图应该可以帮助您更好地理解这一点。首先,请注意,对于给定的满量程值,10 位系统的步进比 12 位系统的步进宽 4 倍。在 12 位系统中,A 点和 B 点之间的差异为 4 LSB,而在 10 位系统中仅为 1 LSB。因此,公式 1 和 2 告诉我们,INL 为 4 LSB 的 12 位系统引入的误差等于 INL 只有 1 LSB 的 10 位系统产生的误差。
从 INL 误差的角度来看,这两个系统具有相同的性能。但是,这并不意味着这两个系统完全相同。例如,12位系统的最大量化误差 比10位系统小四倍(或者说12位系统的量化噪声功率小16倍)。
为了更容易地计算精度,我们可以使用以下等式:

这可以简化为:

由于转换误差等于满量程值除以 2^6,我们可以说其精度为 6 位。具有 6 位精度的三位 ADC 意味着什么?这意味着我们的 3 位 ADC 产生的误差与 INL 为 1 LSB 的 6 位 ADC 产生的误差相同。也就是说,我们ADC的步进是精确控制的(优于ADC的位数)。因此,ADC 仅引入了超出其量化误差的少量误差。
同样,我们可以使用公式 3 计算 ADC 精度并得到:
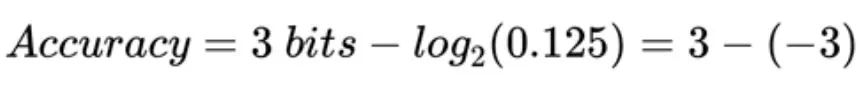
分段和两步 ADC 简介
让我们从稍微不同的角度来研究上述 3 位 ADC,以更好地理解为什么可能需要比分辨率更高的精度。
假设我们有一个理想的三位数模转换器 (DAC)。我们可以使用此 DAC 将 ADC 输出转换回模拟信号。从原始模拟输入中减去 DAC 输出,我们可以找到 3 位量化器的量化误差(或“残留”信号)。这在图 3 中进行了说明。
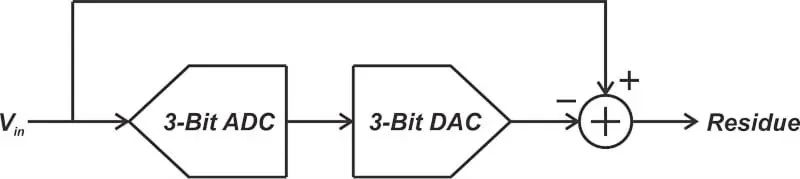
(显示从 ADC 输入减去 DAC 输出的“残留”信号的示例图)
虽然 ADC 的分辨率只有 3 位,并引入了较大的量化误差,但其线性误差相对较低。由于量化误差是主要的误差来源,因此可以通过第二个 ADC 进一步处理残留信号,以产生高于 3 位的整体分辨率。这是可能的,因为 3 位 ADC 的线性误差不会破坏我们的信号。我们只需要将 3 位 ADC 的大量化误差再数字化一次,即可获得更精细分辨率的整体 ADC。这实际上是分段和两步 ADC 的工作原理。图 4 显示了这些 ADC 的更详细框图。
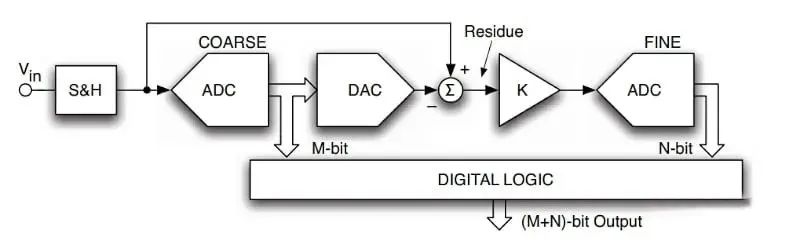
(分段和两步 ADC 的示例框图)
第一个 ADC 执行粗略转换并确定最终输出中最高有效位 (MSB) 的 M 位。然后残留信号由第二个 N 位 ADC 处理。第二级执行精细转换并生成输出的 N 位 LSB。这种结构允许我们用转换速度换取功耗和硅片面积。例如,两步架构需要的比较器数量明显少于全闪存转换器。
对于两步架构,粗略 ADC 的精度需要比其分辨率好得多。除了粗ADC,DAC和减法器对残差信号的精度也起着关键作用。这就是为什么要仔细确定每个模块的最大允许误差,以实现一定的整体精度性能。
现在我们已经确定了分辨率和精度之间的差异,让我们看一个简单的例子,看看我们如何计算具有非零偏移和增益误差的 ADC 的精度。
使用 TUE 评估精度—非零偏移和增益误差
根据设计目标,可以使用绝对精度或相对精度定义来计算公式 3 中的“误差”项。实践中常用的更好选择是 TUE 规范。可以使用增益、偏移和 INL 误差的最大值的和方根 (RSS) 来计算最大 TUE。这可以在下面的等式中看到:
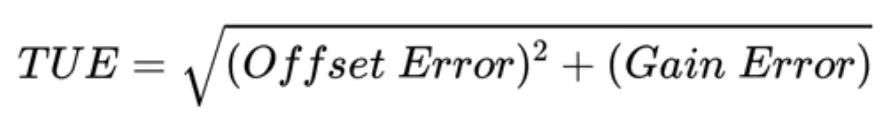
RSS方法基于误差项不相关的假设,因此所有误差项同时处于最大值的概率很小。例如,使用这种方法,我们可以假设对于 12 位 ADC,我们有:
1.INL = 3 LSBs
2.Offset error = 2.5 LSBs
3.Gain error = 3 LSBs
假设应用于 ADC 的模拟输入可以在 ADC 的整个输入范围内取值,我们可以将总误差估算为:

现在,应用等式 3,我们得到:
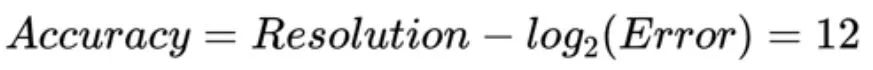
我们有时将公式 3 得到的精度称为“精度的有效位数”。如果我们应用校准来抵消偏移和增益误差,我们将只剩下 INL 误差。请注意,为了使用 TUE 方程,所有误差项都应以相同的单位(上例中的 LSB)表示。
实际上,ADC 只是误差源之一。其他几个组件(例如输入驱动器、电压基准等)可能会增加额外的误差,因此必须予以考虑。
审核编辑:汤梓红
 电子发烧友App
电子发烧友App





















评论