友情提示,运放电路的噪声分析还是比较复杂的,不论是基础理论还是对应的推导过程,都不是特别容易。考虑到兄弟们的基础参差不齐,所以我还是尽量说清楚点,这样导致看起来就有点罗里吧嗦,也会看起来超级复杂,希望不会劝退。
1、关于噪声我想过的几个问题
我一般是带着一些问题去学一些东西,找答案,个人感觉这样主动式的要比被动式的理解更为透彻。说下我之前想过的一些问题吧,这些问题也会在后面得到解答。
问题1:白噪声是随机的,并且是全带宽的,如果某个时刻,正好是各个频率噪声的波峰叠在一起,那噪声电压不是无穷大?概率虽然低,可能性是存在的吧,但是我们好像不会在电路设计中考虑这个问题。
问题2:一般运放手册给出的噪声参数有两种,分别是电压噪声频谱密度和电流噪声频谱密度,单位分别是伏特除以根号赫兹,和安培除以根号赫兹。这个是什么意思,如何转化为我们常规理解的电压信号呢?

问题3:运放的噪声跟构成的电路增益有关吗?会不会被放大?
问题4:对于一个具体的运算放大器放大电路,如何评估输出端的电压噪声大小?
我们就带着上面的问题来学习下。
2、噪声参数与分析基本原理
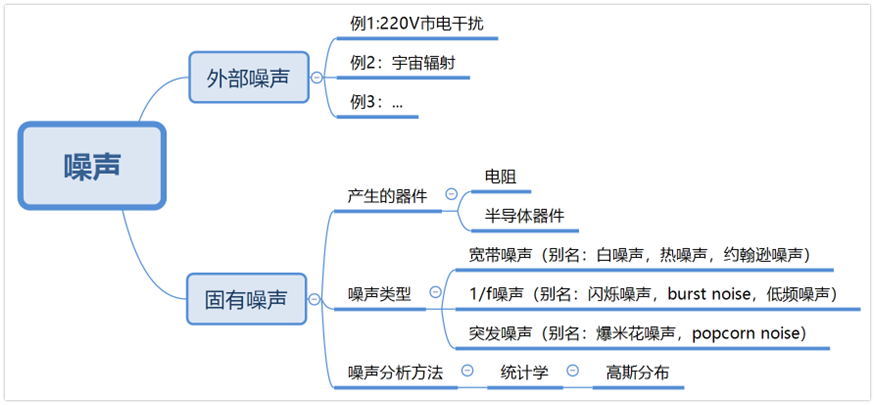
a、噪声类型
噪声可以分为两类:外部噪声和固有噪声,我们本节主要评估运放的固有噪声。
外部噪声:外部电路或自然因素导致的噪声,比如220V的市电干扰,宇宙辐射都是外部噪声。外部噪声很难估计。
固有噪声:固有噪声是由电路的元器件引起的,比如电阻和半导体器件都可以产生噪声。固有噪声可以估计。
b、噪声波形特点
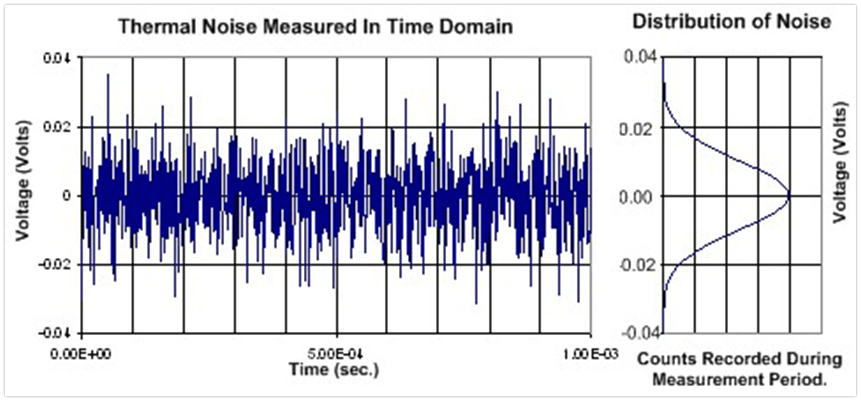
宽带噪声波形(高斯分布):
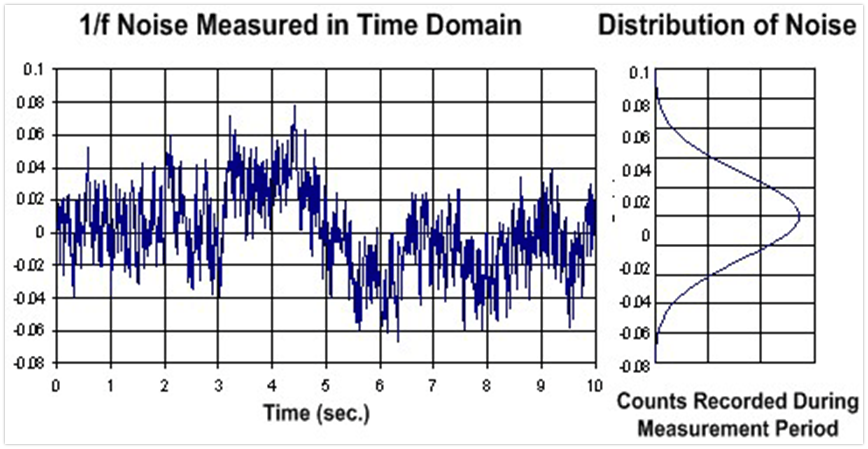
1/f噪声波形(高斯分布):
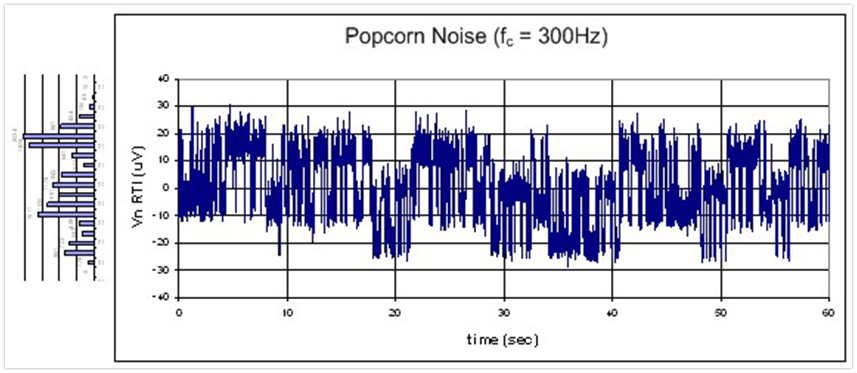
爆米花噪声波形(几个高斯分布叠加):
可能看这个图一下子有点蒙,噪声的波形倒是很直观,但是右边那个旋转90°的正态分布是个什么啥意思?这就不得不说噪声的分析方法。
c、噪声的分析方法
我们在电路中通常需要评估电路噪声在时域的峰峰值。但是噪声又是一个随机的过程,幅度随时间变化而变化,我们没办法预估一个噪声信号在某一个时刻的瞬间值,所以我们是在统计学的基础上对噪声进行分析的。
啥叫在统计学的基础上分析呢?就比如我们丢硬币,正面和反面是随机的,没法预先知道我们下一次丢硬币到底是正面还是反面,但是我们知道各自的概率是50%,如果实验次数足够多,那么最终正面和反面的次数各占总次数的50%。
现在我们评估的噪声也是随机的,我们也没办法知道下一刻噪声信号具体长什么样子,但是我们可以评估,如果我们拿示波器去采样这个信号的话,会知道它落在某一个电压范围的概率是多少,根据这个概率信息,我们可以推断出我们的噪声的峰峰值是多大。
在电路分析中,使用概率分布函数将均方根噪声转化为峰峰值噪声。如下图,左边为噪声的时域波形,右边为高斯分布,高斯分布也叫正态分布。
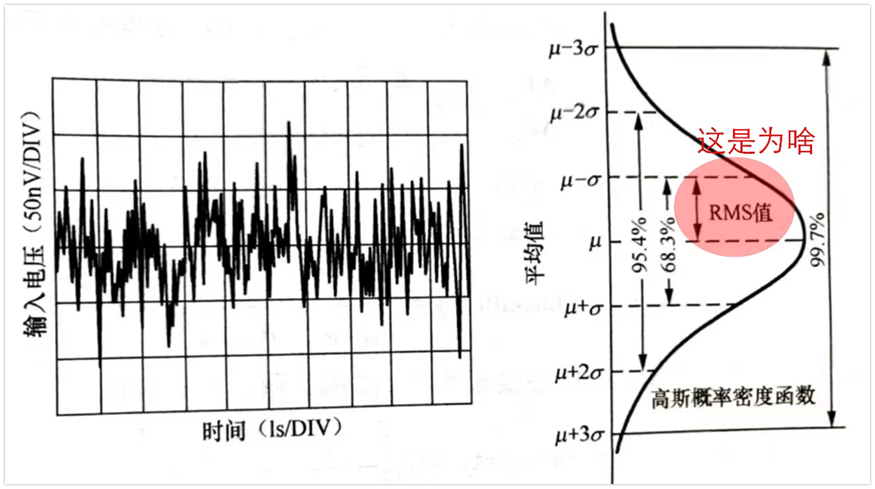
正态分布有两个参数,一个叫期望值μ(也叫平均值),另外一个参数叫标准差σ,图中有一个非常重要的地方,那就是RMS值等于标准差σ(μ=0)。
d、为啥噪声的有效值Vrms等于其正态分布的标准差σ呢?
这可以从有效值的这个词的意义里面推导出来。
有效值:如果某个交流电,与某个电压的直流电热效应相等,那么就可以认为该直流电的电压就是这个交流电电压的有效值。
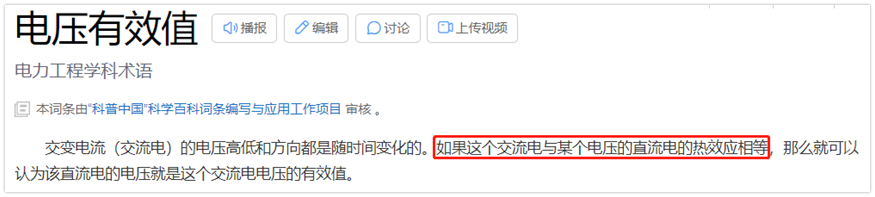
从有效值的定义看,有效值是热效应的等效,也就是针对做功来说的。
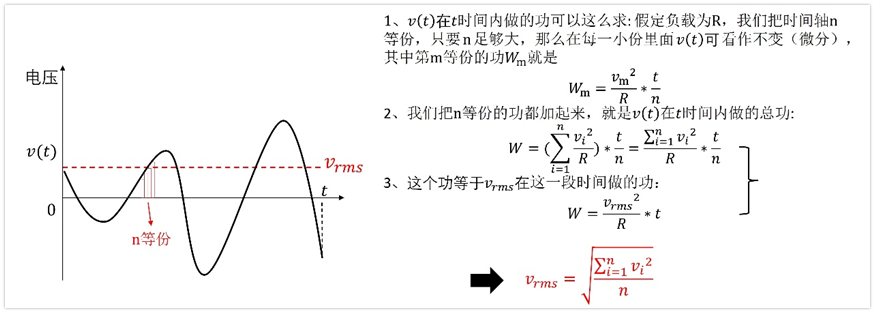
我们再看标准差的公式:
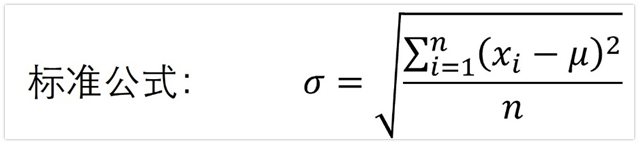
前面说了,噪声电压符合高斯分布,用统计学的方法来看,有下面的推导过程:

以上过程只是为了理解一句话:噪声的有效值Vrms等于其正态分布的标准差σ。
上面推导过程看着有点费劲,看不明白记住也行,这也不是本节内容的重点。
总之,我们就是知道了:噪声电压的有效值等于其正态分布的标准差σ,那这有什么用呢?
回到我们的目标——我们要知道噪声的峰峰值有多大。
我们通常可以计算出噪声的有效值有多大,但这不是我们的最终目的,我们的最终目的是要知道噪声的峰峰值有多大,这是我们设计电路时更关心的。在我们知道了有效值,那么也就知道了噪声电压对应正态分布的标准差,最终我们就能知道某个时刻噪声电压在某个范围内的概率有多大。
还记得大学教材《概率论与数理统计》最后面附表里面的“标准正态数据分布表”吗?我在网上找了一个更为精确的正态分布表,精确到了小数点15位,如下图:
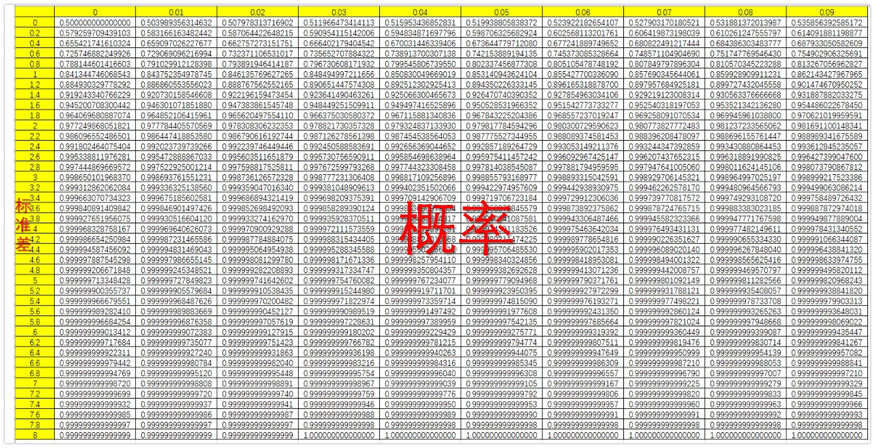
我们可以从中得到峰峰值电压小于某一个值的概率,如下表所示:
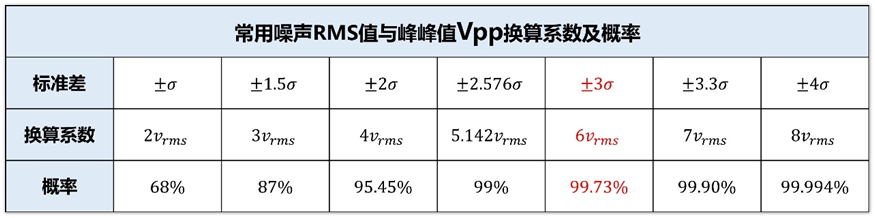
可能还是不太明白这个表是啥意思?简单说就是,我们对有效值为Vrms的噪声进行采样,其采样值落在-σ到+σ之间的概率是68%,落在-2σ和+2σ之间的概率是95.45%,落在-3σ和+3σ之间的概率是99.73%。这意味着幅值很大的电压值出现的概率很小,比如落在-4σ和+4σ的概率是99.994%,即电压超过±4σ的电压出现的概率是0.006%,这个概率是很低的。如果我们拿示波器去测量这个电压,在示波器界面可能是看不到超过±4σ的电压信号的,毕竟示波器采样的数据量有限,除非说我们观察非常久的时间,可能捕捉到一个更高的电压信号,但通常我们也不会这么干。
从前面的正态分布表也可以知道,采样值落在8σ内的概率已经是99.9999999999999%,也就是说电压值超出±8σ的概率是0.0000000000001%。
基于上面的概率问题,一般评估噪声的峰峰值电压是±3σ对应的换算系数,也就是认为噪声的峰峰值为6*vrms,如果对噪声容忍程度非常低,可以用±4σ或更高的换算系数。
以上就是使用统计学评估噪声的基本原理,到这里已经可以回答前面的问题1:
问题1:白噪声是随机的,并且是全带宽的,如果某个时刻,正好是各个频率的波峰叠在一起,那噪声电压不是无穷大?概率虽然低,但可能性是在的吧,但是我们好像不会考虑这个问题。
答:如果用统计学的方法看,因为正态分布两边是无限延伸的,这种情况也是存在的。但可以想象,出现这种概率是有多么多么的小,毕竟噪声电压在±4σ外的概率已经低到了0.006%。从前面15位精度的正态分布表看,到了±8σ的概率已经低到了0.0000000000001%,至于问题里面无穷大电压的场景,应该只具有数学上的可能性,现实中是不会出现的了。
为了避免没抓到重点,这里先小结一下:
电压噪声服从高斯分布(正态分布),并且其有效值Vrms就对应高斯分布的标准差σ。再结合高斯分布的特性,我们一般可以认为电压不超过±3σ,即电压不超过6*Vrms,即评估噪声的时候,可以按照噪声电压峰峰值为6*Vrms。
到这里,那么剩下的问题就是如何计算噪声的有效值Vrms了。
器件一般以频谱密度的方式给出,比如下面是ti的芯片tlv9061给出的噪声参数:

可以看到,噪声的大小是跟频率有关系的,不同频率段的噪声大小不同。除此之外,除了0.1Hz~10Hz是直接以峰峰值给出的,单位是uVpp,这个理解起来完全没问题。另外两个,一个是电压噪声密度,单位是nv/(根号Hz),另外也是fA/(根号Hz),理解起来就相对困难,我就想厂家为什么这么给参数呢?直接像0.1Hz~10Hz这样给出峰峰值大小不香吗?这是故意要提高使用门槛吗?
e、噪声参数为什么以根号hz的方式给出?
可以看到,上面是芯片tlv9061规格书中表格的数据,其规格书也给出了噪声参数的曲线,我们来看一下。
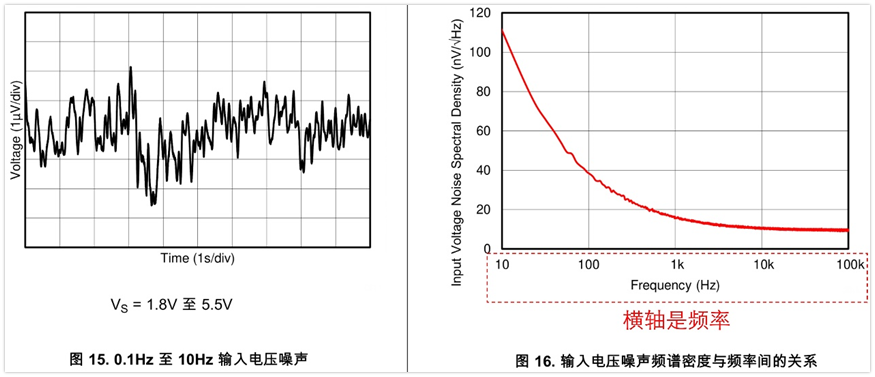
看右边的图,横轴是频率,纵轴是电压噪声频谱密度,下面来看下其物理意义吧。

以上解释了为什么噪声电压密度的单位为什么是V/根号Hz,如果要用简短的话概括,那就是:电压有效值是针对做功来说的,而做功相关的参数就是功率谱密度,单位是V^2/Hz或A^2/Hz,功率谱密度开方就是电压/电流幅度谱密度(假定负载是1Ω),单位是:V/根号Hz和A/根号Hz。
需要注意,上面的推导非常的不严谨。要想真正严谨的理解,需要去看大学教材《信号与系统》的第6章节。
值得一提的是,第1步到第2步用到了帕斯瓦尔定理:
现在我们已经知道了上图中的电压噪声频谱密度的物理意义,那么如何将这个转化为Vrms值呢?
f、如何将电压噪声频谱密度转化为Vrms
其实这个转化在上面图片中第3步已经写明了,就是这个式子:

需要注意,上面的积分范围0~∞,是全带宽积分,实际应用中要根据实际的频率范围。看着这个公式不是很直观,下面就以运放为例子来画一个示意图吧。
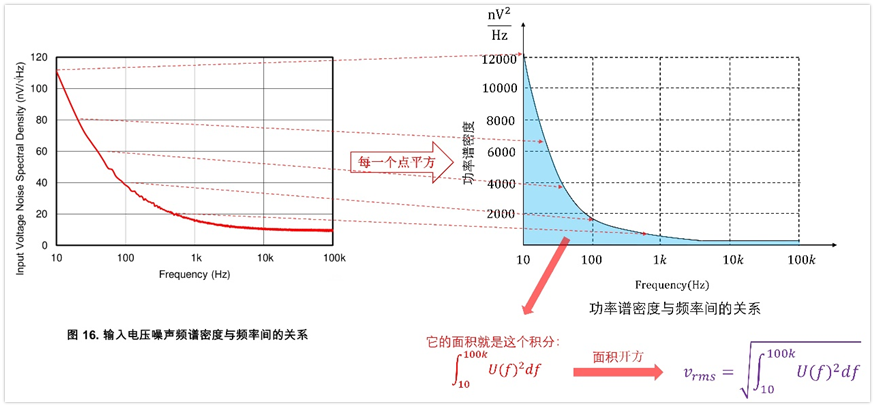
根据运放手册提供的电压噪声频谱密度,我们将每一个点进行平方,就可以得到右边的功率谱密度,然后在频率上进行积分,这个积分过程就等效为求图中阴影部分的面积,然后我们将求得的面积进行开方,就能得到噪声电压的有效值了,图中计算了从10hz~100Khz带宽内的噪声电压有效值。
实际应用中,我们通常不会求全带宽的,因为实际电路也不是全带宽的,我们实际通常求的是一段带宽范围内的,因此,常用的是下面这个:

上面的过程看着很复杂,只是为了说明最基本的原理,实际评估运放噪声会有一些近似的办法的,这个后面会讲。
总之,将电压噪声频谱密度转化为有效值的原理就是:将电压噪声频谱密度进行平方,转为功率谱密度,然后在带宽范围内积分(求面积),再开方,就能求得有效值电压了。
g、如何将电流噪声频谱密度转化为Irms
电流噪声频谱密度转为电流有效值Irms,其实原理和电压噪声频谱密度的转换一样,因为功率P=U^2/R,也等于P=I^2*R,如果按照前面的过程推一遍,电阻R也是可以消掉的,最终可以求得电流有效值为:

3、两种噪声源
说完了如何将噪声电压频谱密度转化为有效值电压Vrms,以及如何将电流噪声频谱密度转化为有效值电流Irms的原理及公式。
还有个问题,那就是运放电路到底有哪些噪声需要评估呢?只有运放的噪声需要评估吗?
噪声我们一般要评估两种,一种是运放的噪声,一种是电阻的噪声。
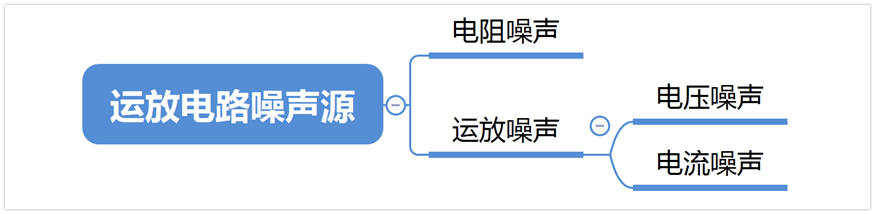
下面来继续具体说下如何将它们转化为Vrms和Irms。
4、运放本身的噪声Vrms,Irms计算
运放的噪声有电压噪声和电流噪声,如下图是ti的运放芯片tlv9061给出的噪声参数,给出的是电压噪声频谱密度和电流噪声频谱密度。

也给出了对应的电压噪声密度曲线:
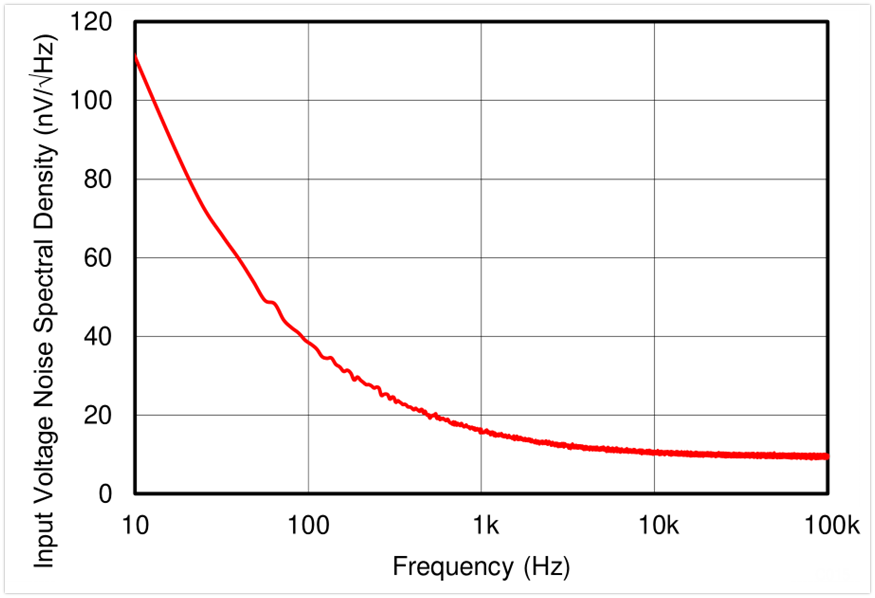
前面我们已经知道了求运放噪声的基本原理:将噪声电压频谱密度进行平方,转为功率谱密度,然后在带宽范围内积分(求面积),再开方,就能求得有效值电压了。
问题是这个求面积可操作性实在是太差了,这个面积很不好求,那么有什么办法呢?
办法自然是有,那就是将上面的曲线分成两部分,分别是1/f噪声和宽带噪声,如下图所示。
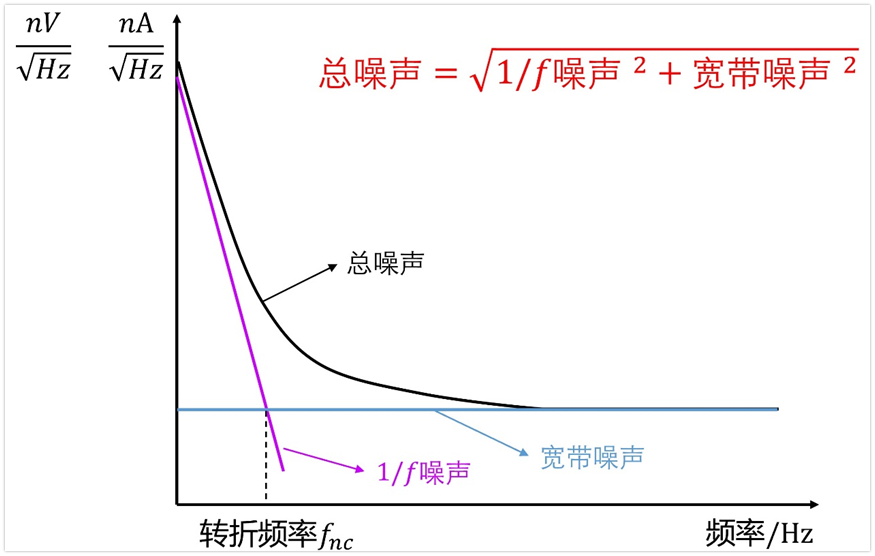
我们在手册中看到的电压噪声频谱密度曲线可以看作是1/f噪声和宽带噪声的叠加(平方后相加再开根号),叠加起来之后的曲线看起来不规则,导致我们难以计算。所以真正计算噪声的时候,我们又需要将这个噪声分解为1/f噪声和宽带噪声两部分。
a、宽带噪声Vrms_bw的计算
因为宽带噪声曲线是平的,很好计算,就先看宽带噪声的计算方法吧。
既然宽带噪声密度曲线是平的,也就是说其是一个常量,用字母B来表示吧,那么其在频率fa~fb频带内的噪声可以用下面公式计算:

举个例子:求tlv9061在0.1Hz~100Khz频带内的宽带噪声电压有效值?
首先从曲线上看出,在10Khz以后,噪声电压频谱密度为10nV/根号赫兹,这个就是宽带噪声电压频谱密度,即对应上面公式的B=10nV/根号赫兹。
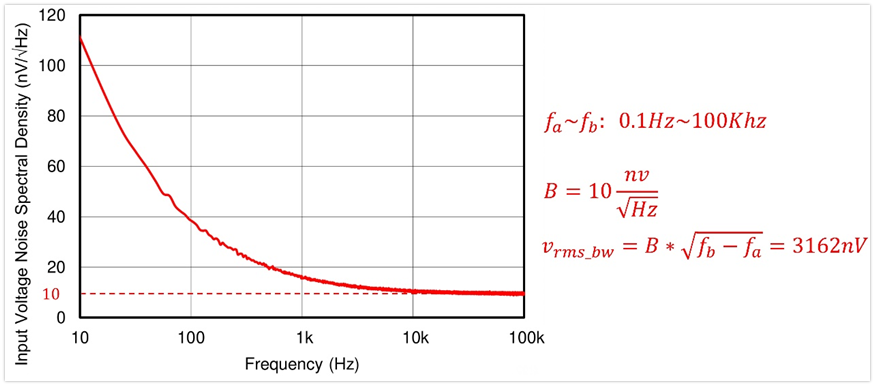
套用上面的公式,最终可求得在0.1hz~100Khz带宽内的宽带电压噪声有效值为3162nV。
b、1/f噪声Vrms_1/f的计算
再看看啥叫1/f噪声。
顾名思义,1/f噪声,说的就是功率谱密度曲线与频率之间满足1/f的规律,注意,这里是功率谱密度,不是电压频谱密度。如果是电压频谱密度,那么就是满足1/(根号f)的规律。
如果在频率1Hz处的1/f电压噪声频谱密度是A,那么根据1/f的规律,频率f处的1/f电压噪声频谱密度值有如下关系式:
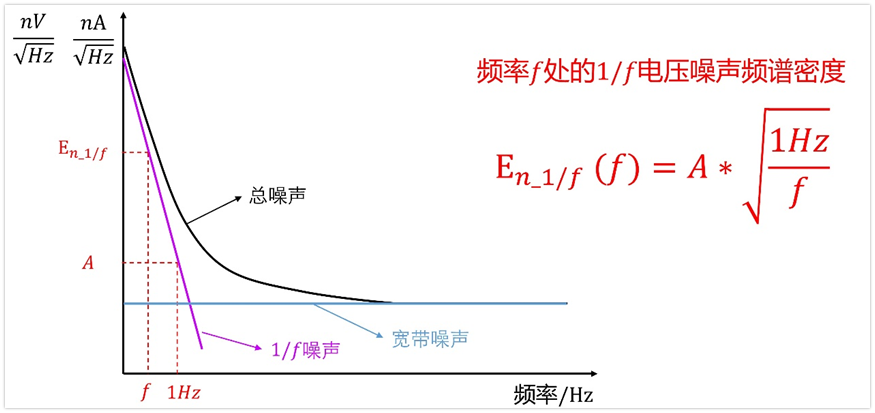
根据上面这个式子,我们就可以得到一定频率范围内1/f电压噪声的有效值,计算方法如下:

还是以tlv9061举例子:求tlv9061在0.1Hz~100Khz内的1/f电压噪声有效值?
规格书中只给了10Hz~100Hz的电压噪声频谱密度曲线,因此,无法直接从图中得到1Hz的电压噪声频谱密度A,规格书的数据表格也没有提供这个参数,那怎么办呢?
其实我们可以从1/f噪声的定义推测出来,我们可以先求得10Hz处的1/f噪声,然后根据前面的1/f噪声频谱密度公式推算出来A的大小。
具体过程如下:
首先从曲线上面可以得到10Hz处的总的电压噪声频谱密度为:E10hz(总)=110nV/根号hz,然后我们又知道10Hz出的宽带电压噪声频谱密度为:10nV/根号hz。再根据叠加关系,就可以得到10Hz处的1/f噪声。
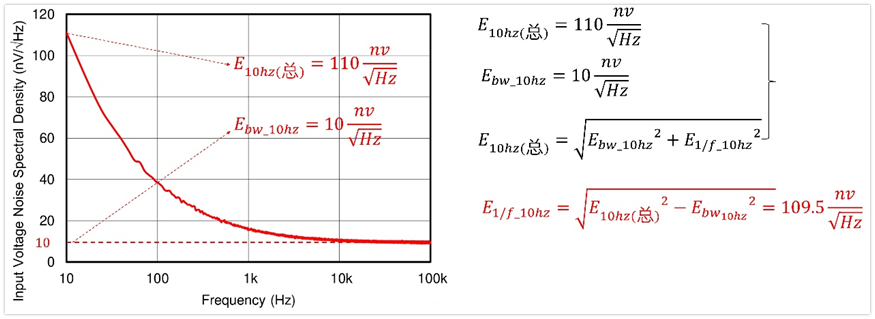
然后根据前面的1/f电压噪声频谱密度公式可求得A的值,再利用Vrms_1/f公式求得最终的噪声电压有效值为1286nV。

c、总电压噪声Vrms计算
前面我们将噪声分解为1/f噪声Vrms_1/f和宽带噪声Vrms_bw,现在已经知道怎么求各自的有效值了,现在还需要将它们合并,求最终的噪声电压有效值。
也很简单,只需要将它们平方之后相加再开根号就可以了,注意,不要直接将两个电压值相加。

为什么不是直接相加?
其实也可以从电压做功的角度考虑,因为做功电压是要平方的,如果直接相加,那么分别计算做的功相加,和电压先相加再计算做的功必然不相等。比如如果二者都是1V,那么分别在R上做的功为:1V*1V*R+1V*1V*R=2R;电压相加做的功:(1V+1V)*(1V+1V)*R=4R,两者是不相等的。
所以按照前面的例子,1/f电压噪声有效值是1286nV,宽带电压噪声是3162nV,那么最终的总电压噪声有效值就是他们俩和的平方根,即3413nV。

e、总电流噪声Irms计算
上面举的例子都是电压噪声Vrms计算,其实电流噪声Irms也是一样的,也是分别计算1/f电流噪声和宽带电流噪声,然后将两者计算平方和根即可。

不过因为前面举例子的芯片tlv9061没有给全电流噪声参数,只有一个1Khz的电流噪声密度值,也没有对应的曲线,所以没办法具体计算。

至于厂家为什么没有标出来,那是因为这个放大器CMOS型放大器,电流非常小,电流噪声就更小了。从上表可以看出,这颗放大器的电压噪声是nV级,而电流噪声是fA级,中间还隔着pA级,也就是说,电流噪声远小于电压噪声,因此电流噪声可以忽略掉。
为了说明电流噪声Irms如何计算,还是举个例子吧。
因为手册中只给出了1Khz时的电流噪声频谱密度为23fA/根号赫兹,从噪声频谱密度曲线形状上我们知道,在低频时噪声密度值随频率升高而下降,高频时噪声密度随频率基本不变,其约等于宽带噪声。由此我们知道这个放大器的宽带噪声密度肯定是小于23fA/根号赫兹的,我们暂且就用23fA/根号赫兹这个参数计算宽带噪声,知道这个计算出来的值要比实际情况大就好。
最终计算0.1Hz~100Khz的宽带电流噪声有效值Irms_bw为7.3nA,计算过程如下

d、带宽确定
到这里已经说明了如何求得fa~fb频带内的噪声有效值,那问题来了,为什么不求0~∞带宽的噪声有效值呢?而只求一部分?
下限频率fa
为什么下限频率fa不能是0呢?
这是因为,我们是从统计学的方法分析的噪声,如果最低频率为0,那么意味值时间为无穷大,这显然不符合常理。另外一方面,如果fa=0,那么其电压噪声频谱密度为无穷大,这也是没法计算的。
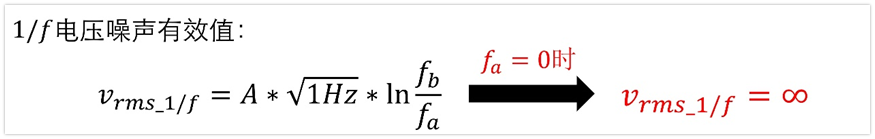
工程上认为,当噪声频率低于0.1Hz,即10s以上发作一次的事件,一般可以被认为是人为、环境因素带来的扰动,这可能与运放电路本身无关。因此,绝大多数情况下,计算1/f噪声,下限取值为0.1Hz。
上限频率fb
上限频率fb为什么不能是无穷大呢?
首先,如果上限是fb,那么不论是1/f噪声,还是宽带噪声,最终的结果都会是无穷大,这也是不符合常理的。
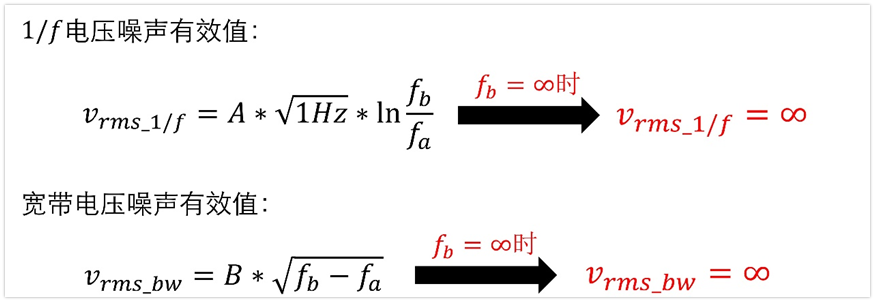
另外一方面,我们的运放电路本身都是有上限截止频率的,类似于一个低通滤波器,还记得运放有一个参数增益带宽积GBW吗?频率到一定程度,运放都放大不了信号的。
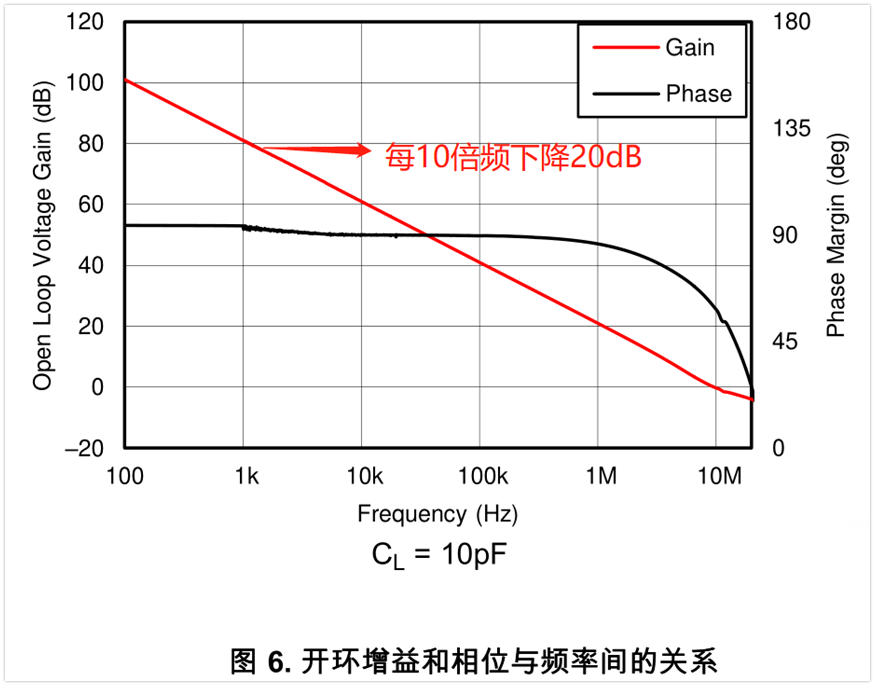
如下图是tlv9061的开环曲线,频率超过100Hz之后, 每10倍频下降20dB,这个特性跟一阶低通滤波器是一样的。
当然,运放一般不是在开环的时候用,我们再看看闭环电路的增益情况。下图是tlv9061手册中的闭环增益曲线,可以看到,闭环增益为10倍时,在1Mhz以后,也是每10倍频下降20db,其曲线像是一个截止频率为1Mhz的低通滤波器。
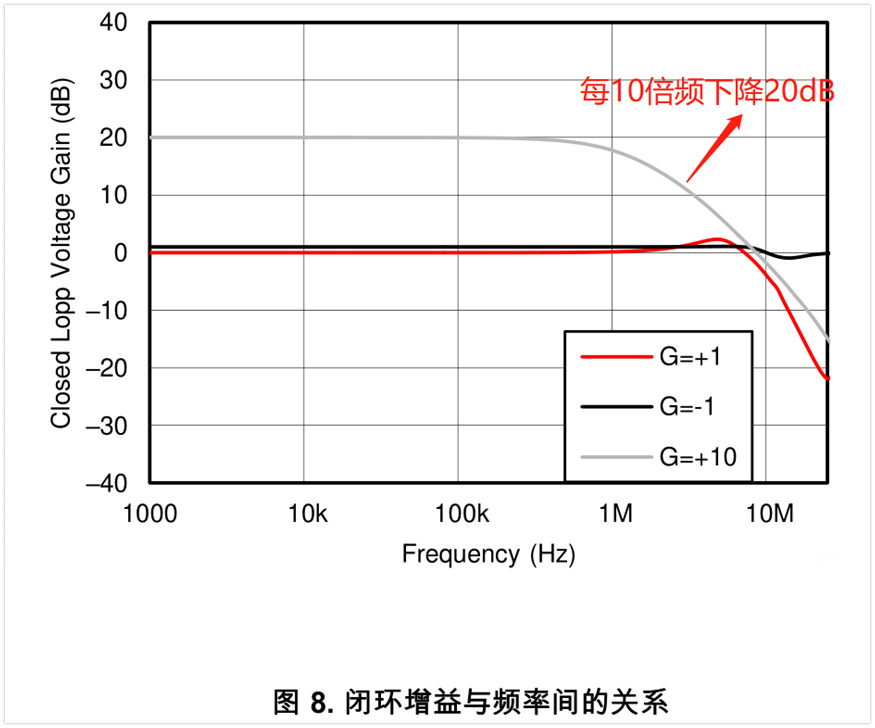
总之,我们在使用运放的时候,其最终的幅频特性就类似一个低通滤波器,其截止频率就是闭环的带宽。这个滤波器也会滤掉高频的噪声,所以说评估噪声的时候,不能认为噪声上限是无穷的,我们要确定好上限频率fb。
那问题来了,上限频率是等效滤波器的截止频率吗?
答案是否定的,因为滤波器的截止频率一般说的是3db的,3db往后噪声只是被衰减了,并不是没有了。
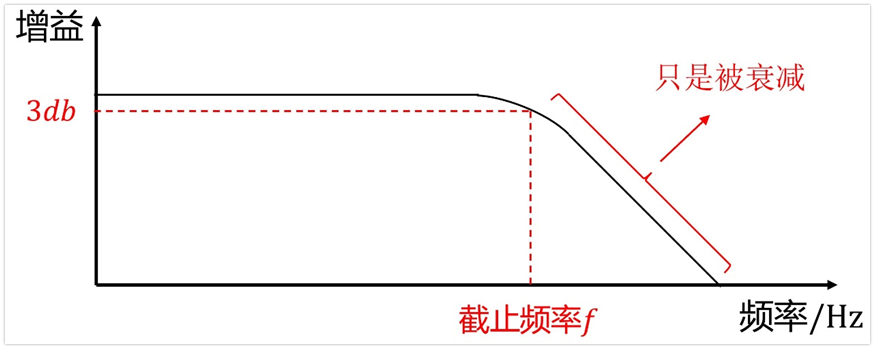
如果说高于截止频率之后,增益立马变为0,那么上限频率等于截止频率没问题,但问题是现在这个滤波器并非砖墙滤波器(频带内完全不衰减,频带外完全衰减为0),所以,如果我们直接草率的让上限频率fb等于截止频率,那么是不符合实际的。
可能会有同学认为,截止频率之后看着幅度衰减很快,忽略也不要紧吧?其实不然,因为这是个对数坐标轴,也就是说频率增大10倍才下降20db,从截止频率下降20db的频率范围其实很宽,因此不能忽略。
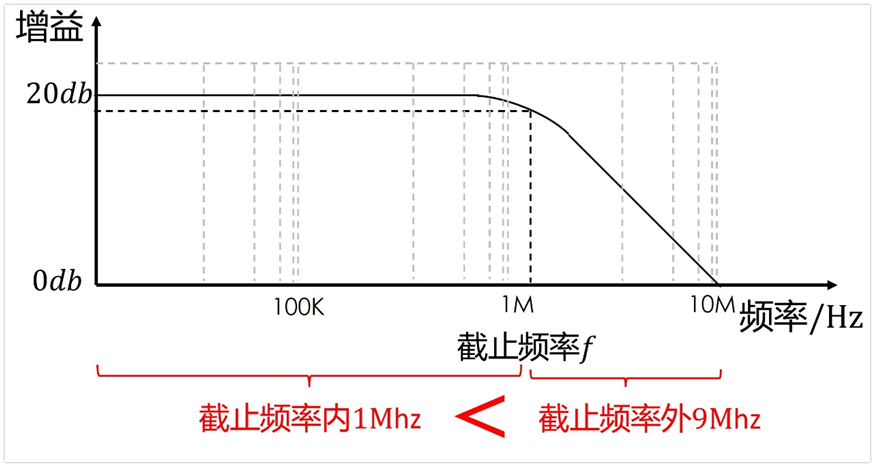
既然问题不能忽略,那又尬住了,这个上限频率fb咋办?
可以用等效的方法,原理如下:假设有一个砖墙滤波器,其截止频率为fh,如果其带宽内的噪声电压有效值等于这个滤波器的噪声电压有效值,那么我们就可以把这个fh看作是我们要的上限频率fb。
结合前面铺垫的基础,只需要让下面两部分的面积相等,就能求得fh和f截止的关系,进而就能求得上限频率fb=fh了(注意,下图的纵轴是电压频谱密度的平方,并不是增益曲线,其形状应该是增益平方后对应的形状)。
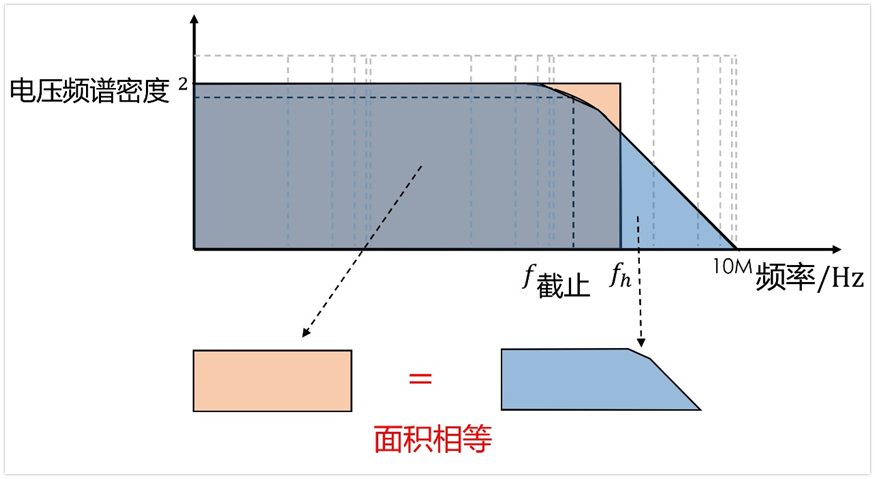
后面的等效计算完全就是个数学问题,这里就不推导了,直接拿结论来用吧,fh=1.57*f截止,即上限频率是滤波器截止频率的1.57倍。
注意,这里的数学计算是将噪声看成是宽带噪声来算的,忽略了1/f噪声,因为在高频段,1/f噪声的贡献本身非常小,所以忽略是没问题的。
其次需要注意,如果我们的电路本身就是滤波器电路,并且阶数不是一阶,那么这个系数也需要对于的变化。这应该比较容易明白,如果是高阶滤波器,那么曲线更陡峭,更加接近于砖墙滤波器,其系数应该更小。
下面是各种滤波器的系数:

举个例子:现用tlv9061设计了一个放大5倍的放大器,电路本身并非是滤波器电路,请问其评估噪声的时候带宽是多少?
答:如前面的分析,频率下限按照fa=0.1Hz;查看手册,TLV9061的增益带宽积是10Mhz,放大倍数为5倍,所以其闭环增益带宽为:10Mhz/5=2Mhz,这个电路本身并非滤波器,因此等效为一阶滤波器,截止频率为2Mhz,再乘以一阶滤波器的系数1.57,可求得频率上限fb=1.57*2Mhz=3.14Mhz。
总之,我们在评估带宽的时候,下限可以按照0.1Hz来评估。上限要看电路本身是否是滤波器,如果不是滤波器,可以先求得对应的闭环带宽,然后乘以对应的系数,就能得出上限频率了;如果是低通滤波器,则直接用滤波器的截止频率乘以对应的系数,也能得到上限频率。
5、电阻的噪声Vrms_r的计算
关于运放的噪声已经说明白了,那么电阻噪声呢?
电阻噪声一般说的是热噪声,也是白噪声,其特点是各个频率的噪声能量相同,即噪声密度是一条平坦的曲线。它的RMS值与带宽的平方根成正比,随着带宽的增加,电阻的噪声会成为电路噪声的主要因素。
电阻的电压噪声有效值计算相对简单,只跟电阻阻值的大小,温度,带宽三者有关,可以用下面公式计算:

我们也可以根据上面的公式,反推得到电阻的电压噪声频谱密度公式,下图即是电阻的电压噪声密度公式,以及常见电阻在25℃下的电压噪声频谱密度。
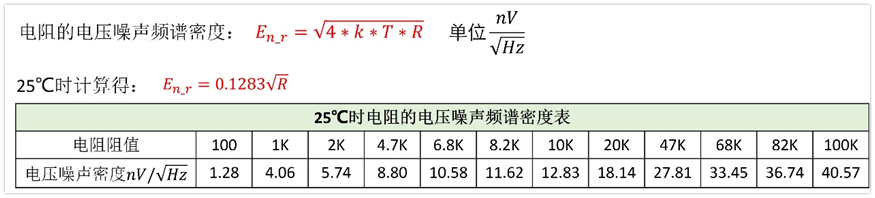
实际电路设计中,我们可以根据上表快速的近似估算电阻的噪声大小。
根据上面的公式,我们可以推导出:无论并联,串联,只要最终总的电阻阻值一致,都是不会改变电阻的热噪声的,过程就不证明了。
6、总的电压噪声输出计算
至此,我们已经知道如何求得运放,电阻各自的电压噪声有效值,但这还不是我们最终的目的,我们需要知道的是我们设计的电路输出的总的电压噪声大小。
其实后面就简单了,我们只需要将噪声源加到电路当中去就可以了,然后利用叠加原理分别计算不同噪声源对输出噪声的贡献,最后就可以求得最终输出端的总噪声大小了。
a、放大器电路噪声模型
下图是常见的同相放大器放大电路:
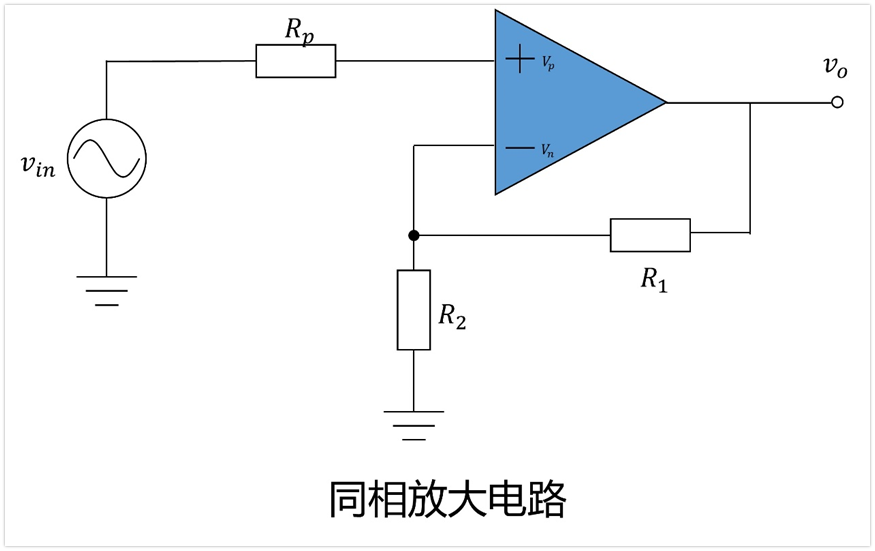
我们给每个电阻加上电压噪声,给放大器加上电压噪声和电流噪声,最终可构建如下图所示的电路噪声模型。
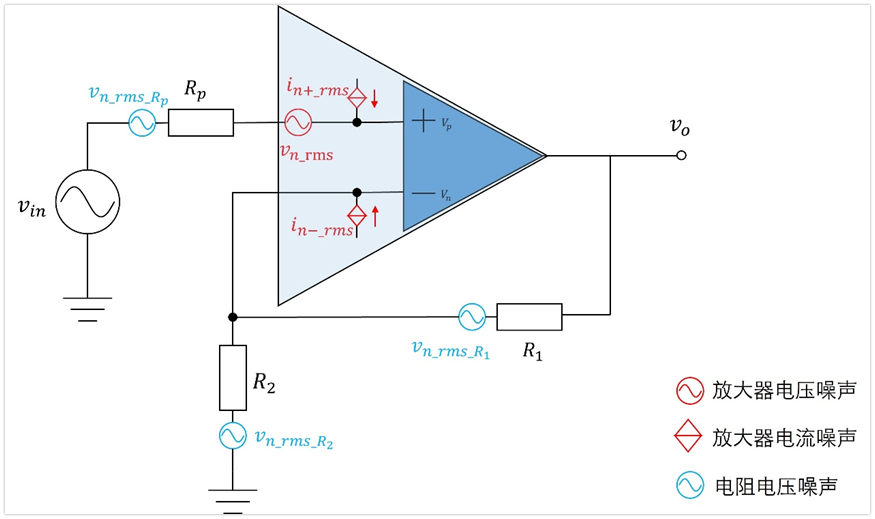
这里需要提一点,我们前面已经知道了运放的电流噪声有效值Irms如何计算,但是这个模型里面是有两个电流噪声的,分别是同相端电流噪声in+_rms和反相端电流噪声in-_rms,一般我们认为计算出的电流噪声Irms=in+_rms=in-_rms。
加上所有的噪声信号之后,这个电路看起来非常复杂,看着有点头大,那么输出端总的电压噪声该如何计算呢?
b、放大器电路的总噪声有效值Vn_rms_out
其实开头已经说了,我们只需要将噪声源加到电路当中去就可以了,利用叠加原理然后分别计算不同噪声源对输出噪声的贡献,就可以求得最终输出端的总噪声大小了。
具体如何求呢?
上图中有3个电阻,就有3个电阻电压噪声,然后放大器同相和反相端各有1个电流噪声,还有一个运放的电压噪声,总共6个噪声源,我们要分别求这6个噪声源在输出端产生的噪声大小。
因为我们电路是线性电路,因此满足叠加原理,可以求得6个噪声的表达式如下,然后将这些噪声求平方和,然后开根号,就能得到我们最终总的输出电压总噪声Vn_rms_out了。
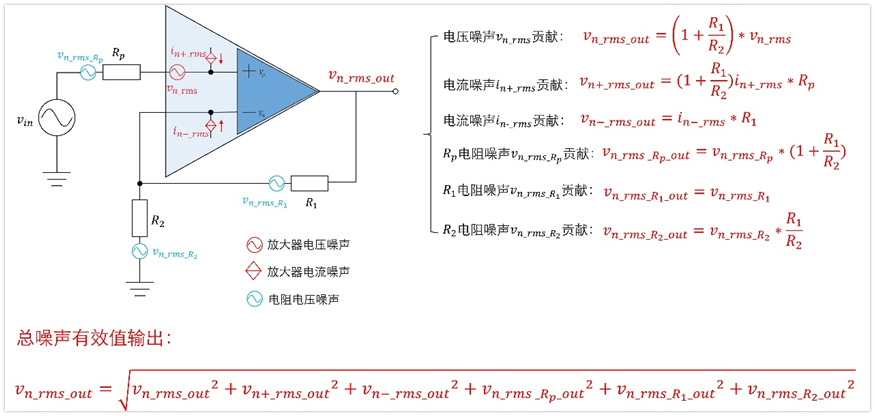
这里有个问题,不是利用叠加原理吗?为什么最终总的电压噪声有效值不是将这6个直接加起来呢?而是取平方,累加之后再开方呢?
其实原理跟1/f噪声和宽带噪声叠加的原理一样,我们现在计算的6个噪声都是有效值,合并之后计算总的输出也是有效值,既然都是有效值,那么就是叠加后要满足做功相等,所以就是平方后累加再开方。
下面写明了如何求得6个噪声的表达式,其实如果对运放的虚短和虚断理解清晰,应该就不在话下了。
1、放大器电压噪声Vn_rms对输出端的贡献Vn_rms_out
单独评估放大器电压噪声Vn_rms对输出端的贡献,那么我们令其它的噪声不存在,电压噪声统统视为短路,电流噪声通通视为断路。同时我们是评估噪声的影响,那么令输入信号也为0,即输入接地,最终等效电路如下图:
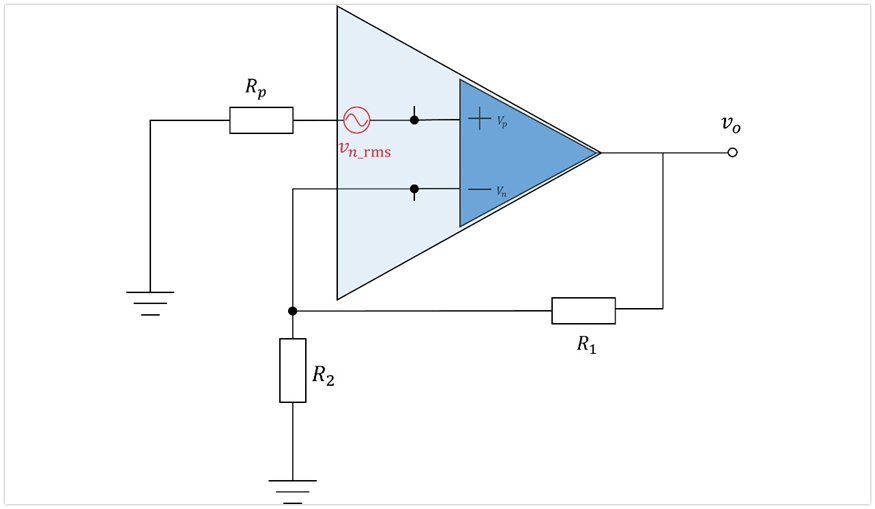
根据运放的基本特性,我们很容易就能求出Vn_rms在输出端的贡献电压了,过程如下:
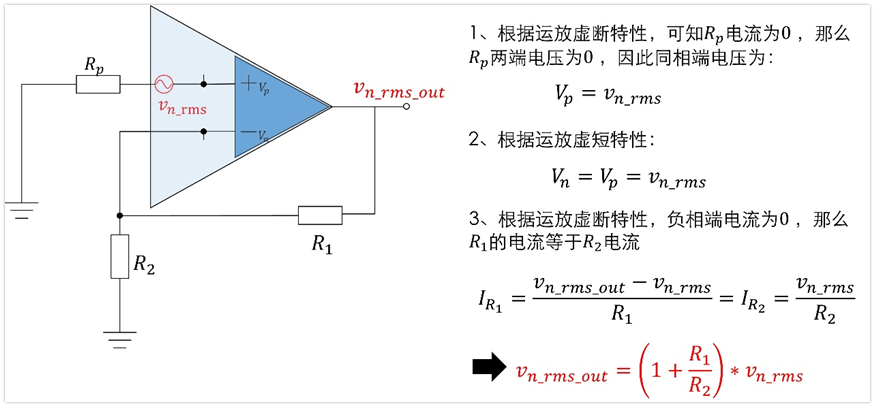
上面这个电路其实就是个常见的同相放大电路,放大倍数就是1+R1/R2,输入信号是Vn_rms,上面的过程我只不过是按照运放虚断和虚短的基本特性又推导了一遍而已。
继续看剩下的5个噪声对输出的贡献。
2、放大器正相端电流噪声In+_rms对输出噪声的贡献Vn+_rms_out
同样的道理,其它的电压噪声视为短路,电流噪声视为开路,输入接地,电路图变成如下:
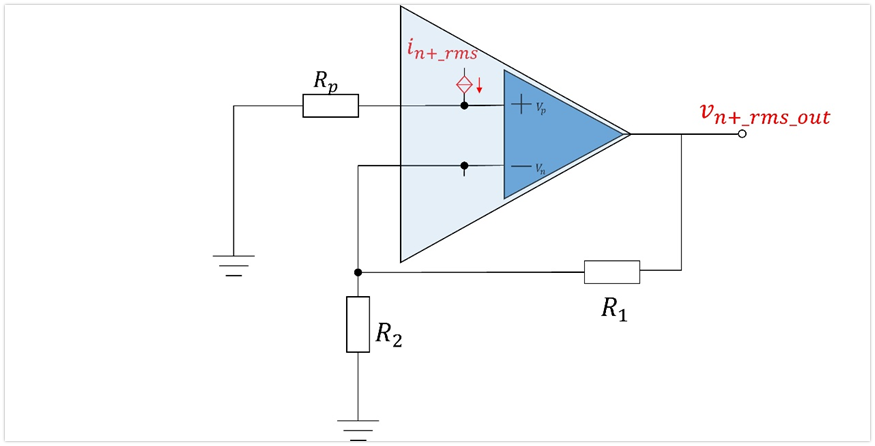
很容计算出正相端电流噪声在输出端的贡献如下:
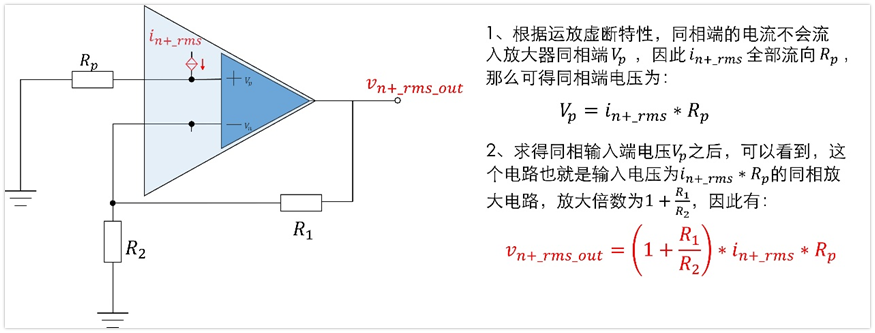
3、放大器负相端电流噪声In-_rms对输出噪声的贡献Vn-_rms_out
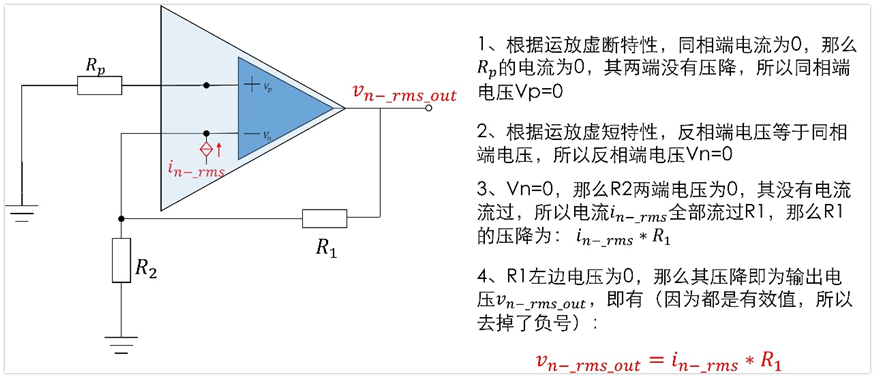
4、电阻Rp的噪声Vn_rms_rp对输出的贡献Vn_rms_rp_out
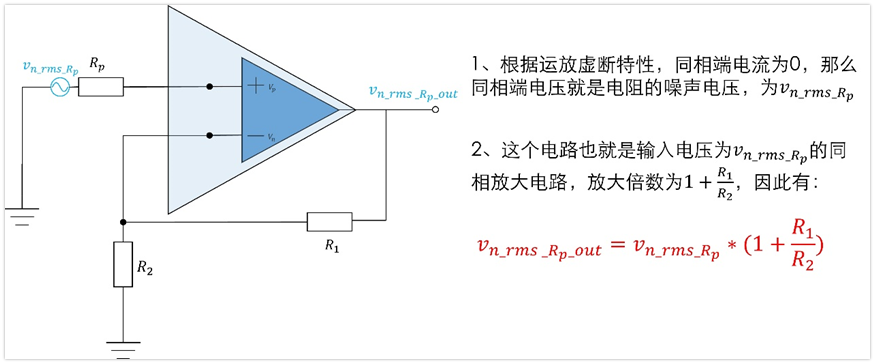
5、电阻R1的噪声Vn_rms_r1对输出的贡献Vn_rms_r1_out
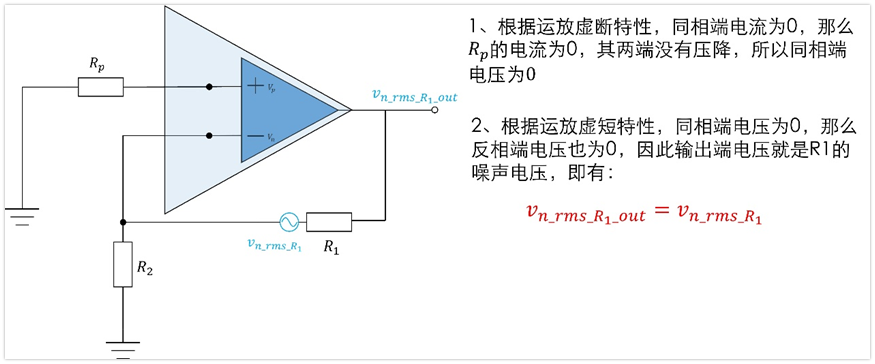
6、电阻R2的噪声Vn_rms_r2对输出的贡献Vn_rms_r2_out

可以看到,如果运放的AoL不是无穷大,那么实际电路的闭环增益是和电阻有关系的。我们代一些具体的值进去看看影响有多大,假设R2=1K,R1=9K。开环增益从1到1百万时,闭环增益的情况如下图:
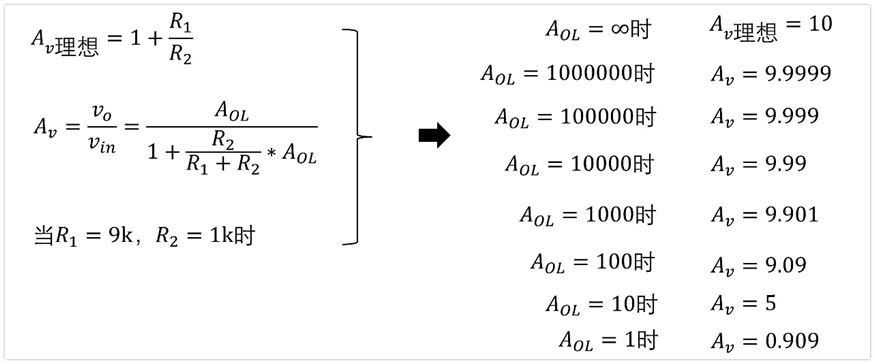
从上面至少可以看到两点:
a、在AoL比较小的时候,实际增益就与理想情况下的增益有明显差异了。比如如果AoL=1000,实际闭环增益Av=9.901,与我们想象的放大10倍就已经有1%左右的差异,如果AoL=100,实际Av=9.09,差不多有10%的差距了。
b、在AoL比较大的时候,一致性要求低。尽管AoL=100万和AoL=10万二者相差了10倍,但是闭环增益一个是9.9999,一个是9.999,相对于理想情况下的10来说,误差都非常小。也就是说只要运放开环增益AoL足够大,闭环增益都基本稳定在同一个值,正是因为这样,我们对运放的开环增益AoL的一致性要求就很低了,只要求大就可以了,不管是50万倍还是100万倍,闭环增益都基本一样。我们实际运放的AoL也确实没那么精确。
以LM2904为例,如下图,其典型开环增益AoL是140V/mV=14万倍,最小值为7万倍,如果考虑温度,那就只有3.5万倍,至于上限,都是没有标出来的。总的来说,就是器件的开环增益一致性比较差,但是因为够大,也不影响我们使用。

除此之外,我们还应该看到第3点:
c、闭环增益越大,要求AoL越大。上面是放大10倍的情况,闭环增益误差1%时对应的开环增益是1000。假如我们放大100倍(即设计闭环增益=100倍),要求实际运放闭环增益与理想运放只有1%的差距,那么需要AoL≈10000(此时闭环增益Av=99)。相对于10倍只需要AoL=1000,此时AoL=10000提高了10倍。这可以自己算一下,就不再写出来了。
之所以前面写了这么多,就是因为运放的AoL本身就不是固定的,它跟频率有关系,这也就造成了运放的使用有了限制。
还是以LM2904为例,手册表格中的AoL=140V/mV=14万倍=20log(140000)=102db。手册还给出了AoL与频率的关系曲线,如下图:
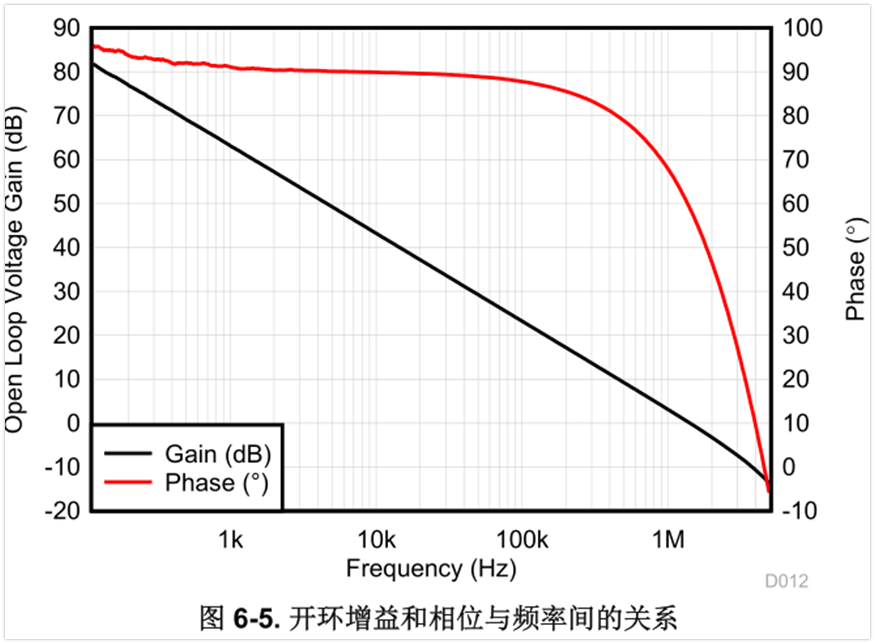
从图中可以看到,AoL随频率是一直在下降的,最左边的频率为100Hz,开环增益AoL=82dB左右,相对表格中的直流开环增益AoL=102dB,下降了20dB,也就是10倍。频率为1Khz的时候,AoL=62dB左右,相对直流AoL下降了40dB,也就是100倍。
极端一点,在1.2Mhz的时候,AoL=0dB,也就是说,这个运放没有放大作用,开环增益为0,既不放大,也不衰减。这个频率点也就是运放的单位增益带宽,也是运放的增益带宽积。
所以呢,我们在使用运放的时候,我们要看我们放大信号的有效频率是多大,如果过大,在对应频率处运放的实际AoL可能就比较小,导致实际增益达不到我们的目标,电路也就失效了。
实际电路如何考虑
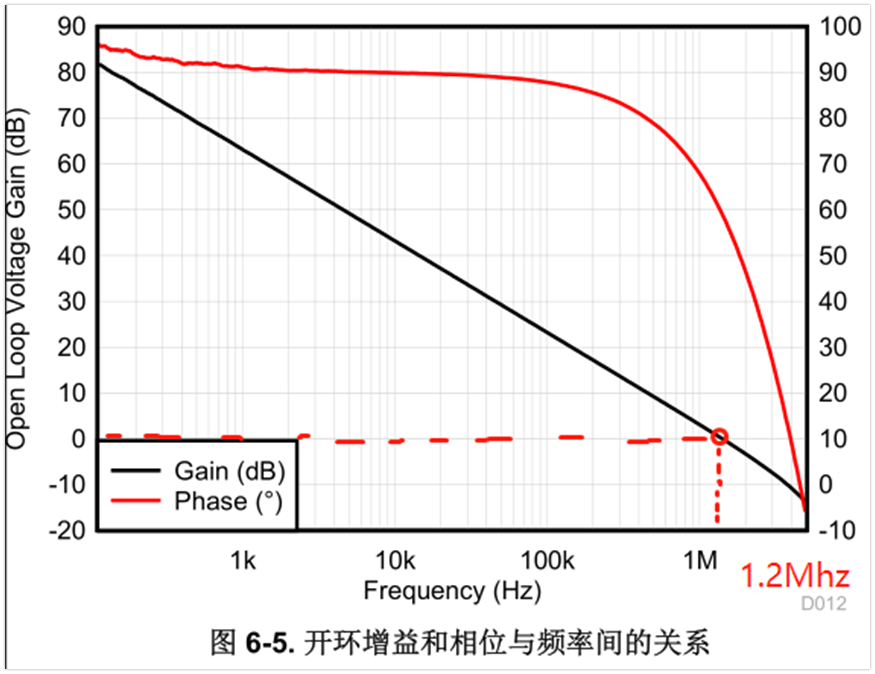
运放基本都给出了一个参数叫增益带宽积,比如LM2904是1.2Mhz

除此之外,曲线上面也能看出来,对应开环增益为0db的点就是增益带宽积GBW,也是单位增益带宽。
前面的章节只是为了说明道理,我们实际设计电路的时候,一般用这个增益带宽积就够了。
举个例子:
问:假设我们要求电路放大10倍,有用信号最大频率是10Khz,那么这个带宽积GBW=1.2Mhz的运放能满足要求吗?或者说如果要放大10倍,用这个运放最大可以放大多大频率的信号?
答:
1、f=10Khz,Av=10倍,计算f*Av=100khz < 1.2Mhz,这个运放是可以满足要求的
2、GBW=1.2Mhz,Av=10倍,计算f=GBW/Av=120Khz,即这个情况下运放最大可以放大120Khz的信号,频率高了增益就会下降。
需要注意,这个计算本身就是极限值,因为增益带宽积本身就是3dB时候的,因此此时已经有了一定的衰减,如果完全按照这个计算值来设计,实际得到的增益还是会有所下降的。如果要求特别准确,必须留够充足的裕量。
上面是通过计算的方法,一些手册也列举了闭环增益与频率的关系,我们也可以看图,比如下图是LM2904的曲线。
可以看到,放大10倍的时候,增益下降3db对应的频率大概就是100K多一点,与前面计算的120Khz基本相符合。如果要求增益非常准确,从曲线上看,频率可能只能用到30Khz左右了。
小结
关于运放的增益就写到这里了,主要写了以下几点:
1、啥是开环增益,闭环增益
2、开环增益是如何影响闭环增益的
3、电路设计中如何考虑增益与带宽的问题
审核编辑:汤梓红
 电子发烧友App
电子发烧友App


















评论