0. 这篇文章干了啥?
UAV的最大安全飞行速度是一个关键指标,确保了UAV在执行任务时能够迅速而安全地完成任务,同时保持控制并避免潜在的危险。很明显,具有不同硬件或算法的UAV在不同任务中可能表现出不同程度的效率。为了提高任务执行效率,UAV需要能够在飞行速度高的同时,在环境中进行快速的障碍物检测和避让。在这个过程中,算法延迟、感知范围和定位误差等因素可以显著影响UAV的最大安全速度。
目前,有越来越多的传感器和算法可构成UAV的整个系统。但是,很少有模块在所有方面表现出色。例如,增加感知范围往往会导致延迟增加。因此,在模块选择过程中需要进行权衡。虽然普遍认为UAV的定位误差、感知范围和整体系统延迟会影响其速度,但很少有人能够定量描述这些参数的影响程度。特别是对于定位误差,虽然有很多相关工作致力于提高UAV的定位能力,但如何定量地描述它们对UAV的最大飞行速度的影响仍然是一个问题。这导致在选择新的传感器或算法时很难评估最终的性能,特别是当两个或更多的变量同时变化时(例如,减少定位误差伴随着定位延迟增加)。
在这篇文章中,作者旨在揭示各种参数,特别是定位误差,对UAV的最大飞行速度的影响。作者通过从理论分析的角度建立UAV参数与最大飞行速度之间的关系模型来实现这一目标。此外,作者还分析了这些参数之间的耦合关系。
2. 摘要
无人机(UAV)的最大安全飞行速度是衡量其在完成各种任务时效率的重要指标。该指标受诸多参数影响,如无人机定位误差、感知范围和系统延迟等。然而,在定位误差方面,尽管已经有许多研究致力于提高无人机的定位能力,但对其对速度的影响缺乏定量研究。在这项工作中,我们对无人机的各种参数与其最大飞行速度之间的关系进行建模。我们考虑了类似于穿越密集森林的场景,在这种场景中,无人机需要迅速避开直前的障碍物,并在避让后迅速重新定向。基于这种情景,我们研究了诸如定位误差等参数如何影响无人机飞行中的最大安全速度,以及这些参数之间的耦合关系。此外,我们在模拟环境中验证了我们的模型,结果显示,预测的最大安全速度与测试速度相比误差小于20%。在高密度情况下,定位误差对无人机的最大安全飞行速度有显著影响。这个模型可以帮助设计者使用更合适的软件和硬件来构建无人机系统。
3. 主要贡献
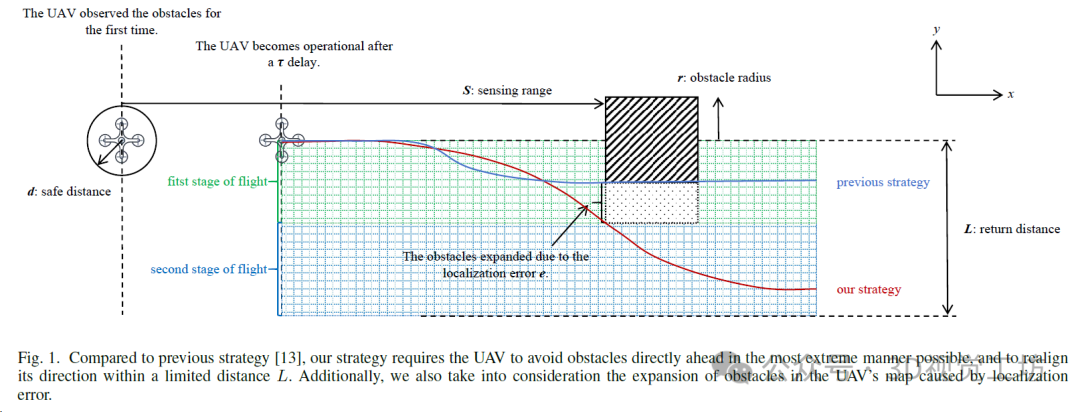
在这项工作中,作者讨论了诸如定位误差、感知范围、算法延迟以及无人机的物理限制对无人机在避障场景中的最大飞行速度的影响。基本场景设置如图1所示。作者使用数学表达式阐明了最大安全速度与这些变量之间的关系。此外,作者提供了关于在不同参数值下最大安全速度趋势的见解,并讨论了在不同条件下各个参数的敏感性。通过比较不同现有的无人机硬件模块,展示了如何利用这个工具进行无人机设计分析。结果表明,通过巧妙地组合组件和分析硬件配置,与简单堆叠性能组件的蛮力方法相比,可以实现更高的无人机安全飞行速度。作者在仿真环境中对该模型进行了测试,结果表明,即使在最大飞行速度为18m/s时,作者的模型仍然可以确保预测的飞行速度误差在20%以内。这项工作是首次从理论建模的角度全面探讨了无人机定位误差、感知范围和算法延迟对无人机最大安全速度的影响。
4. 方法
假设无人机是一个实时系统,仅基于当前观测做出决策。规划者始终希望产生更平滑的曲线飞行,因此可以将无人机避开障碍物的过程分为两个阶段:障碍物避让和快速方向返回。
同时,由于假设无人机具有固定的目标方向速度,这意味着 vx 始终等于 vsafe,并且无人机避开障碍物的总时间为:
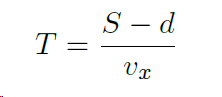
1)障碍物避让: 在这个阶段,无人机需要直接避开前方的障碍物。根据先前的假设,显然,在无人机在配置空间感知到障碍物的那一刻,它距离障碍物的距离为 S - d。减法 s 考虑到了无人机的摄像头未被定位在螺旋桨的边缘的典型情况。在感知到障碍物的那一刻,无人机的碰撞边界已经向前推进了距离 d。因此,在配置空间中,障碍物朝相反方向扩展了 d。
考虑到算法的延迟为 τ,在无人机刚刚避开与障碍物的碰撞的情景中,无人机应该保持最大垂直加速度 amax。有了这个想法,可以得到以下关系:
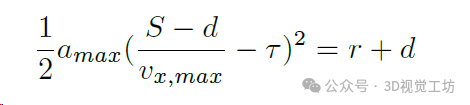
移动 vx,max 到左侧可以得到:
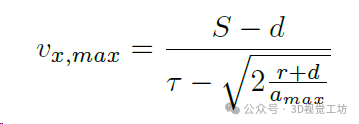
这是无人机在第一阶段接受的最大安全速度。
为了计算碰撞对无人机速度的影响,还需要确定无人机在与障碍物分离的那一刻在 y 方向的速度。由于假设无人机总是以平稳的方式偏离障碍物,规划者始终会生成确切地与障碍物分离的轨迹,在第一阶段的任意时间 t,假设无人机的位置为 (x, y)。因此,可以得到以下关于该时刻无人机的微分方程:
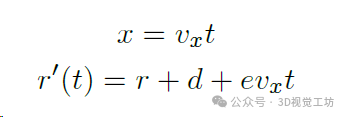
如果 t < τ :ay = 0
否则如果 t > τ :
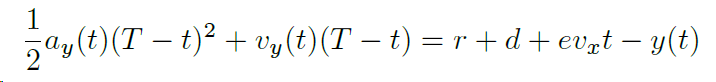
解上述方程得到,当 t > τ 时,表示 y 和 vy 关于时间的变化的函数可以表示为 Y(t) 和 Vy(t):
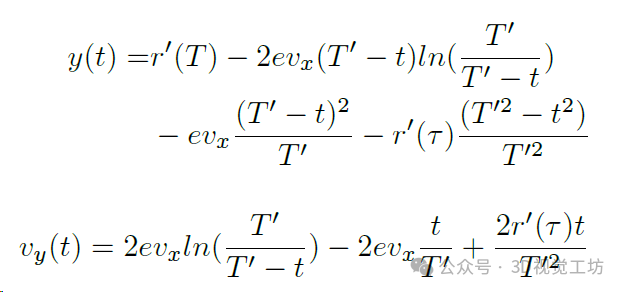
可以观察到,当 t 接近 T 时,y 趋向于 r + evxT,这符合无人机平稳飞行的预期。
然而,如果仔细观察 v 和 a 的变化,会发现当 t 接近 T 时,v 和 a 都趋于无穷大。这个现象实际上是可以理解的。由于定位误差的影响,即使无人机非常靠近障碍物,障碍物仍会以相同的速度扩展。当距离更短时,所需的加速度自然会更大。然而,在实际情况中,无人机的加速度是有限的,因此在达到极限后加速度不会继续增加。无人机的加速性能如图4所示,t' 表示无人机以最大加速度飞行的持续时间。
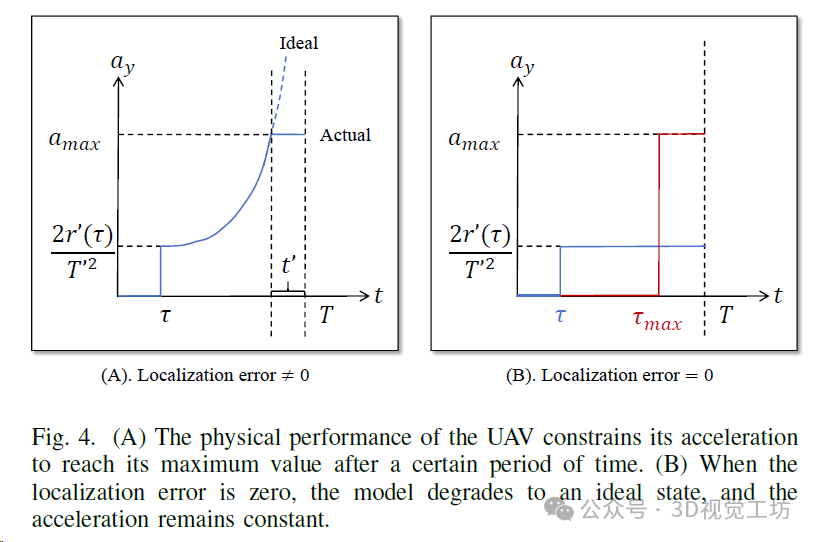
根据加速度的变化可以计算出变化节点,然后可以计算出最终的速度和位置。
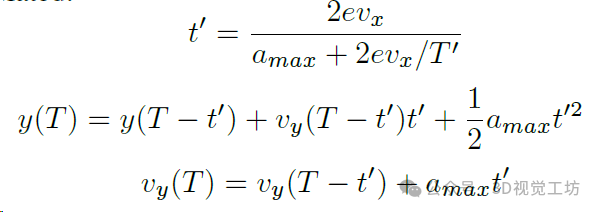
尽管加速度是有限的,但通常 t' 是一个很短的时间。这意味着在大多数情况下,由此产生的位置偏差几乎可以忽略不计。
2)快速方向返回: 在这个阶段,无人机需要在有限距离 L 内将其 y 方向速度减少到零。根据第一阶段的计算得到的 vy(T) 和 y(T),以及对 jerk 的限制,可以轻松地得到以下表达式:
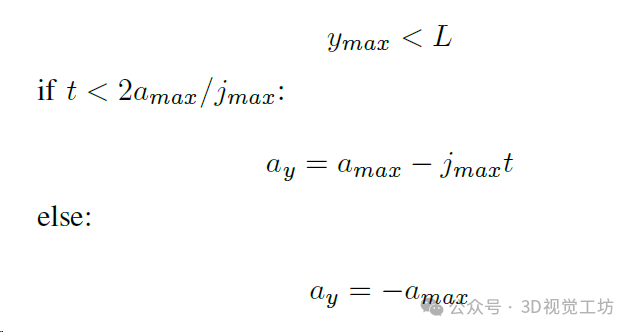
我们可以得到:
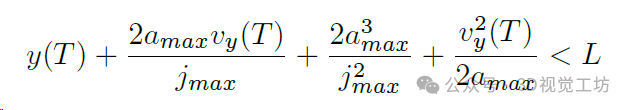
这个约束确定了避免在第二阶段与障碍物碰撞的最大安全速度。
5. 模型分析
A. 飞行状态变化的分析
第一个问题是第一阶段速度分量vx和vy的限制如何反映在最大安全速度上。很容易理解,vx < vx,max确保了在飞行速度不超过vx,max的情况下,无人机不会在第一阶段与障碍物相撞。这由图5.(C)红线的左侧表示。
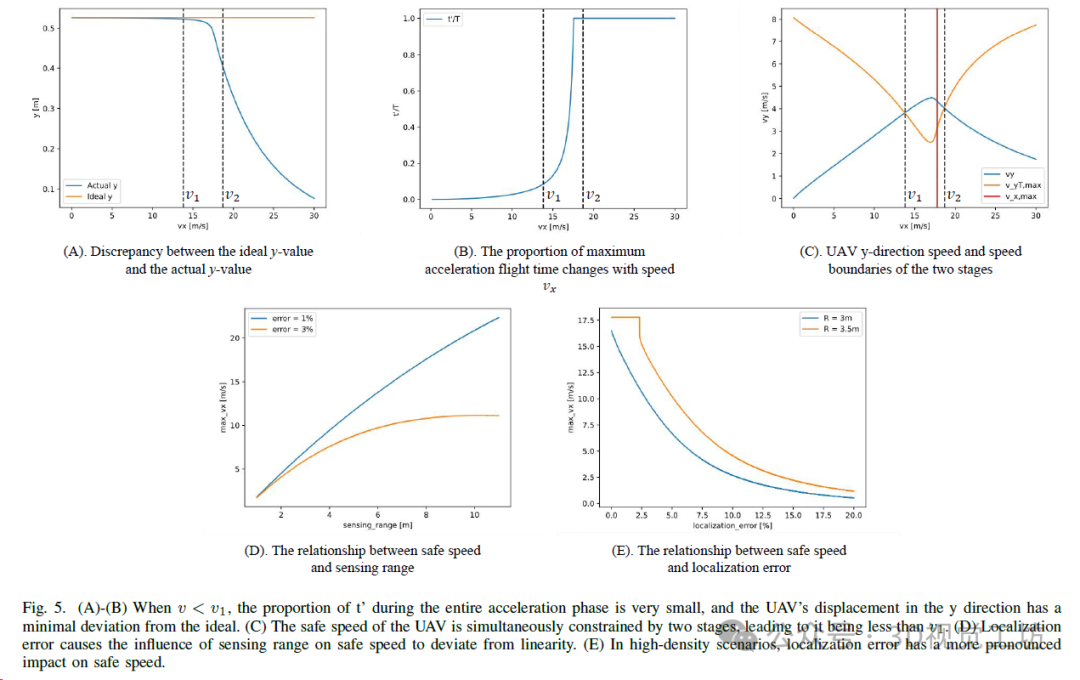
关于vv(T) < vy,max(T),通过在图中将vv(T)和vy,max(T)的曲线作为vx的函数绘制,可以找到两个交点v1和v2。这限制了无人机的速度必须小于v1或大于v2。考虑到避免第一阶段障碍物的限制,如果vy,max(T) > v2,则无人机速度被限制在0到v1和v2到vy,max(T)的范围内。
然而,在现实中,即使出现这种情况,当速度vx超过v2时,无人机在一段显著的时间内无法达到所需的加速度,导致其在y方向的实际位置与理想位置之间存在很大的差异,如图5.(A)-(B)所示。
因此,在规划中,无人机模型与膨胀障碍物重叠一段显著的时间是不合理的,因此速度被限制在0到v1的范围内。换句话说,在上障碍物的限制下,无人机的最大安全速度为v1。
至于为什么vy(T)相对于vx表现出先增加后减少,可以将飞行的第一阶段分为两部分。第一部分遵循理论结果并控制加速度。这部分的加速度曲线与理论计算一致,并需花费T − t′时间。第二部分发生在所需加速度达到无人机极限时,无人机只能尽最大努力飞行。在这部分中,无人机保持最大加速度值amax,持续时间为t′。两部分的总时间为T = (S−d)/vx。
可以想象,随着vx的增加,t′应该先增加后减少。当无人机的速度较低时,随着速度的增加,无人机避开障碍物所需的加速度变得更高。这导致t′在总时间T内所占比例增加,因此t′增加。然而,随着速度进一步增加,t′逐渐占据整个T。与此同时,无人机变得不太能够有效地避开障碍物。更快的速度意味着更短的避让时间T本身,这导致t′的减少。这实际上也导致了vy(T)的衰减。通过将t′与T的比值作为vx的函数绘制出来,如图1所示,可以观察到这种转变确实发生在v1和v2之间。
这意味着v1和v2之间的区域实际上是一个过渡期,在这个过渡期中,无人机逐渐偏离理想控制,其性能接近其极限。
另一个问题是无人机飞行中的偏差,因为它总是非理想的,是否会导致与障碍物的直接碰撞。实际上,当v < v1时,这种偏差是最小的。如果我们将理想位置和实际位置绘制在图上,以侧向速度vx为x轴,我们将得到图5.(A)。可以观察到理论值和实际值之间的差异非常小。这种差异实质上是由障碍物的持续扩展引起的,导致无人机判断错误。在映射过程中发生的"碰撞"部分实际上只涉及短暂的时间重叠,而不是实际的物理碰撞。在安全距离较大的情况下,甚至可能没有任何重叠。
B. UAV参数影响的分析
关于感知范围,根据图5.(D),当定位误差较小时,无人机的速度几乎与感知范围的增加成线性关系增加。这符合在第一阶段的限制中vx < vx,max的表示。
然而,随着定位误差的增加,随着感知范围的增加,飞行速度的改善逐渐偏离线性关系。这是因为更大的感知范围导致无人机更早地观察到障碍物,这也意味着障碍物的扩展更早地发生。因此,无人机的y方向速度变得过高。第二阶段的边界逐渐限制了安全速度的增长。
当涉及到定位误差时,根据图5.(E),它对最大安全速度的影响是明显的。然而,在大多数情况下,定位误差的值很小,在图中的曲线的前半部分得以体现。
6. 实验结果
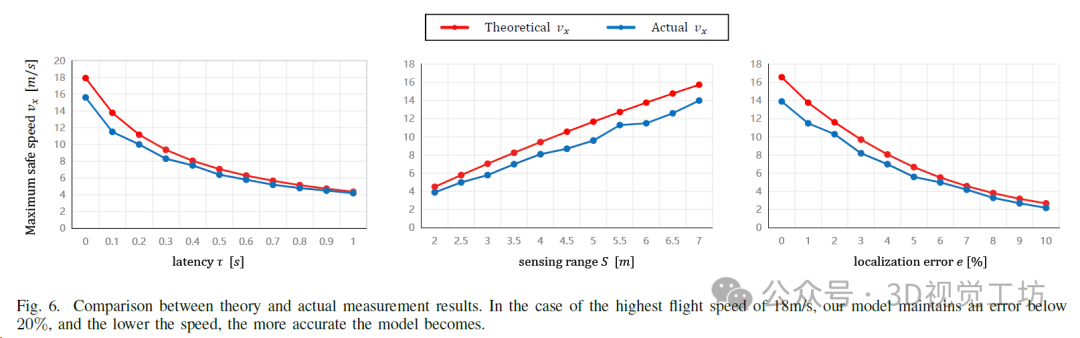
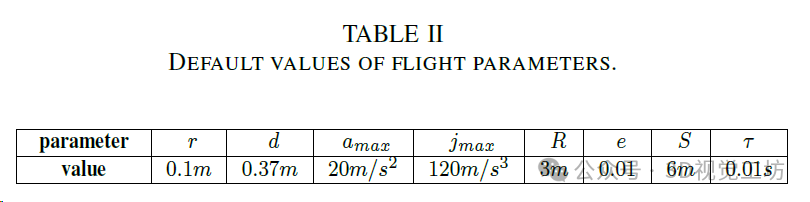
在进行测试后,作者绘制了理论最大安全速度与实际测试的最大安全速度之间的关系,对不同参数进行了图 6 显示。默认参数设置如表 II 所示。在图中,从左到右,表示最大安全速度随延迟、定位误差和感知范围的变化。经过观察,随着飞行速度的增加,模型预测的速度与实际速度之间的差异逐渐增大。在最高飞行速度 18 米/秒下,预测与实际结果之间的差异小于 20%。
导致误差的主要原因是在 UAV 飞行的第二阶段,需要从最大前向加速度迅速过渡到最大反向加速度。这种快速变化导致 UAV 控制过程中存在一定程度的过冲,从而导致实际偏航距离略大于理论距离。
7. 总结 & 未来工作
在这项工作中,作者研究了参数如定位误差、感知范围和计算延迟对无人机的最大安全速度的影响。通过假设典型场景中的障碍物避让和修正机制,作者展示了诸如定位误差之类的参数如何影响无人机飞行。结果表明,随着障碍物密度的增加和无人机飞行空间的减少,定位误差对最大安全速度的影响变得越来越显著。通过对多个参数进行耦合分析,发现优化单个指标并不总是能保证系统的最佳整体飞行速度。考虑多个参数的联合计算可以为无人机设计提供更好的指导。作者在模拟器中验证了其结论,当最大飞行速度达到18m/s时,模型预测的安全速度在20%的误差范围内。未来,作者将进一步验证无人机在真实无人机上的飞行性能。
审核编辑:黄飞
 电子发烧友App
电子发烧友App




















评论