被喻为“重要数据保险箱”的安全芯片已经渗入人们生活的方方面面。随着5G、物联网、车联网的迅速发展,为安全芯片开启了新的应用场景,同时也带来了新的挑战。
本文将带大家深入了解安全芯片的核心,后量子密码认证技术。
1、安全认证技术概述
安全认证技术是防止信息被篡改、删除、重放和伪造的一种有效方法。它使接收者能够识别和确认消息的来源和真伪。目前认证技术主要有4种:
(1)数字摘要
(2)数字摘要+对称密钥认证
(3)数字摘要+非对称密钥认证
(4)数字证书认证
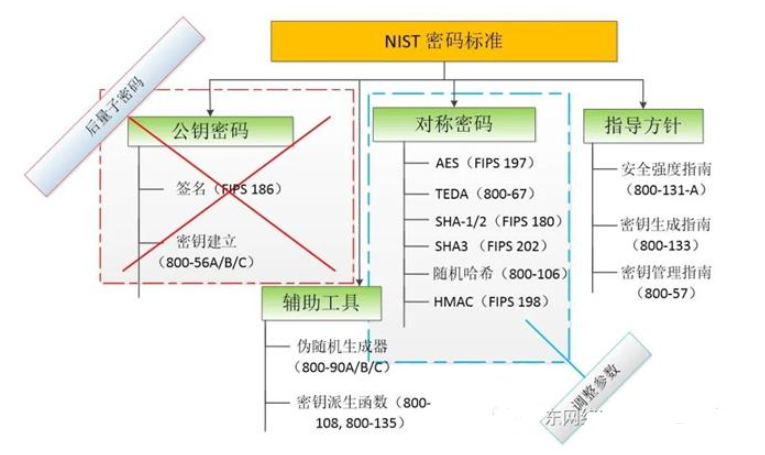
不过随着量子计算机的发展,现有的绝大多数公钥密码算法(RSA、Diffie-Hellman、椭圆曲线等)能被足够大和稳定的量子计算机攻破,也就是说目前基于非对称密钥的认证技术都不安全,会被攻破。所以需要研究基于后量子密码的认证技术。
1.1 数字摘要
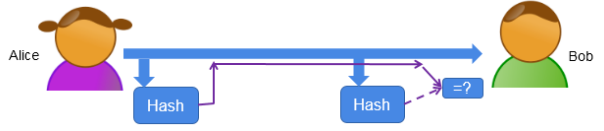
该技术就是使用单向的HASH函数将需发送的消息摘要成为一串固定长度的数据,然后发送给接收方。
具体步骤如下:
(1)使用Hash函数计算消息的摘要,将其与消息一起发送。
(2)当Bob收到消息,使用同样算法计算摘要,与收到的摘要进行比较。
主要优点:
(1)对消息的任何改变,摘要必然变化。
(2)单向函数:无法从摘要构造出原文。
主要缺点:
(1)仅仅Hash没法保证完整性。
(2)改变这个消息,重新计算摘要,用改变后的消息+摘要替换原来的报文。
1.2 数字摘要+对称密钥认证
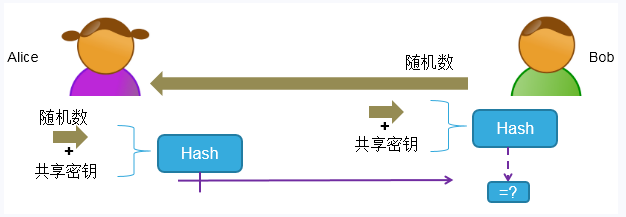
该技术就是使用共享的对称密钥加密随机数,再使用HASH函数将密文信息摘要成为一串固定长度的数据,然后发送给接收方。
具体步骤如下:
(1)通过安全通道,Bob和Alice共享一个密钥。
(2)Bob发送一个随机数给Alice。
(3)Alice用共享密钥加密随机数,并对加密结果进行HASH运算,HASH值发送给Bob。
(4)Bob也用共享密钥加密随机数,并对加密结果进行HASH运算,计算的结果与接收的HASH进行比较,相等则表示是Alice发送过来的。
主要优点:
(1)在确保密钥安全下,可以防止信息被篡改。
(2)分组加密性能快。
主要缺点:
(1)需要通过安全通道共享密钥。
(2)双方都保存密钥,只要一方泄漏密钥即可破解信息。
1.3 数字摘要+非对称密钥认证
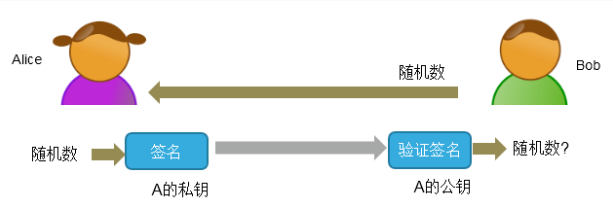
该技术就是使用自己的私钥对发送信息进行签名,然后接收方使用公钥验证这个签名。
具体步骤如下:
(1)Bob拿到Alice的公钥,发送一个随机数给Alice。
(2)Alice收到随机数后用自己的私钥进去签名,签名结果发送给Bob。
(3)Bob使用Alice的公钥对接收的签名进行验签,如果验签通过则确认是Alice发出来的信息。
主要优点:
(1)公钥可以公开,无需保密。
(2)只需发送方保存自己的私钥。
主要缺点:
(1)如何确定公钥来自Alice?易受中间人攻击。
1.4 数字证书认证
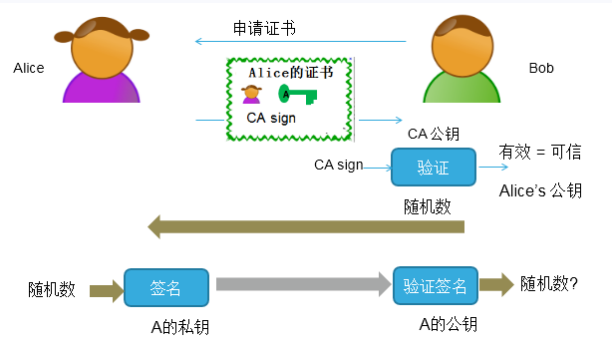
该技术就是需要有一个CA(可信的授权中心),发送方Alice从CA申请证书,CA确认Alice确实是Alice,生成和发布Alice的证书。Alice的证书包含:
· 主题Subject:需要鉴别的个人Alice
· Alice的公钥public key
· 数字签名digital signature:CA对证书的签名
· 发布者Issuer:验证了信息并发布证书的实体
· 签名算法Signature Algorithm
具体步骤如下:
(1)Bob申请Alice的证书公钥。
(2)Alice把自己的证书发送给Bob,Bob收到后使用CA公钥验证证书,并获取得到Alice的公钥。
(3)Bob拿到Alice的公钥后,发送一个随机数给Alice。
(4)Alice收到随机数后用自己的私钥进去签名,签名结果发送给Bob。
(5)Bob使用Alice的公钥对接收的签名进行验签,如果验签通过则确认是Alice发出来的信息。
主要优点:
(1)可以抵抗中间人攻击,确认Alice的公钥。
主要缺点:
(1)无法抵抗量子计算机攻击。
2、后量子密码算法概述
后量子密码是能够抵抗量子计算机对现有密码算法攻击的新一代密码算法。实现后量子密码算法主要有以下 4 种途径 :
(1)基于哈希 (Hash-based):最早出现于1979 年,主要用于构造数字签名。代表算法:Merkle 哈希树签名、XMSS、Lamport 签名等。
(2)基于编码 (Code-based):最早出现于1978 年,主要用于构造加密算法,代表算法:McEliece。
(3)基于多变量(Multivariate-based):最早出现于1988年,主要用于构造数字签名、加密、密钥交换等。代表方法/算法:HFE (Hidden Field Equations)、Rainbow (Unbalanced Oil and Vinegar (UOV) 方法)、HFEv- 等。
(4)基于格(Lattice-based):最早出现于1996 年,主要用于构造加密、数字签名、密钥交换,以及众多高级密码学应用,如:属性加密 (Attribute-based encryption)、陷门函数 (Trapdoor functions)、伪随机函数 (Pseudorandom functions)、同态加密 (Homomorphic Encryption) 等。代表算法:NTRU 系列、NewHope (Google 测试过的)、一系列同态加密算法 (BGV、GSW、FV 等)。由于其计算速度快、通信开销较小,且能被用于构造各类密码学算法和应用,因此被认为是最有希望的后量子密码技术。
当参数选取适当时,目前没有已知的经典和量子算法可以快速求解这些问题。
再次强调,这些算法的安全性,依赖于有没有可以快速求解其底层数学问题或直接对算法本身的高效攻击算法。这也正是量子计算机对于公钥密码算法有很大威胁的原因。
除这4种问题之外,还有基于超奇异椭圆曲线 (Supersingular elliptic curve isogeny)、量子随机漫步 (Quantum walk) 等技术的后量子密码构造方法。另外,对称密码算法在密钥长度较大时 (例如 AES-256),也可被认为是后量子安全的。
为什么上面列的 4 种是最重要的?因为这 4 类途径是最能构造出公钥密码学中已有的各类算法的后量子版本,甚至还能超越(例如基于格的(全)同态加密)等。
1.1 基于哈希 (Hash-based)
基于哈希的签名算法由 Ralph Merkel 提出,被认为是传统数字签名 (RSA、DSA、ECDSA 等 ) 的可行代替算法之一。基于哈希的签名算法由一次性签名方案演变而来,并使用 Merkle 的哈希树认证机制。哈希树的根是公钥,一次性的认证密钥是树中的叶子节点。基于哈希的签名算法的安全性依赖哈希函数的抗碰撞性。由于没有有效的量子算法能快速找到哈希函数的碰撞,因此(输出长度足够长的)基于哈希的构造可以抵抗量子计算机攻击。此外,基于哈希的数字签名算法的安全性不依赖某一个特定的哈希函数。即使目前使用的某些哈希函数被攻破,则可以用更安全的哈希函数直接代替被攻破的哈希函数。
1.2 基于编码 (Code-based)
基于编码的算法使用错误纠正码对加入的随机性错误进行纠正和计算。一个著名的基于编码的加密算法是 McEliece 。McEliece使用随机二进制的不可约 Goppa码作为私钥,公钥是对私钥进行变换后的一般线性码。Courtois、Finiasz 和Sendrier 使用 Niederreiter 公钥加密算法构造了基于编码的签名方案。基于编码的算法(例如 McEliece)的主要问题是公钥尺寸过大。基于编码的算法包括加密、密钥交换等。
1.3 基于多变量 (Multivariate-based)
基于多变量的算法使用有限域上具有多个变量的二次多项式组构造加密、签名、密钥交换等算法 。多变量密码的安全性依赖于求解非线性方程组的困难程度,即多变量二次多项式问题。该问题被证明为非确定性多项式时间困难。目前没有已知的经典和量子算法可以快速求解有限域上的多变量方程组。与经典的基于数论问题的密码算法相比,基于多变量的算法的计算速度快,但公钥尺寸较大,因此适用于无需频繁进行公钥传输的应用场景,例如物联网设备等。
1.4 基于格 (Lattice-based)
基于格的算法由于在安全性、公私钥尺寸、计算速度上达到了更好的平衡,被认为是最有前景的后量子密码算法之一。与基于数论问题的密码算法构造相比,基于格的算法可以实现明显提升的计算速度、更高的安全强度和略微增加的通信开销。与其他几种实现后量子密码的方式相比,格密码的公私钥尺寸更小,并且安全性和计算速度等指标更优。此外,基于格的算法可以实现加密、数字签名、密钥交换、属性加密、函数加密、全同态加密等各类现有的密码学构造。基于格的算法的安全性依赖于求解格中问题的困难性。
在达到相同(甚至更高)的安全强度时,基于格的算法的公私钥尺寸比上述三种构造更小,计算速度也更快,且能被用于构造多种密码学原语,因此更适用于真实世界中的应用。近年来,基于LWE (Learning with Errors) 问题 和 RLWE (Ring-LWE) 问题的格密码学构造发展迅速,被认为是最有希望被标准化的技术路线之一。
3、格密码算法概述
格(lattice)是一种数学结构,定义为一组线性无关的非0向量(称作格基)的整系数线性组合。具体来说,给定一组格基X1,。..。..,Xn对任意的整数C1,。..,Cn,C1X1+.。.+CnXn都是属于这个格的向量,n称为格的维数。例如,下图表示了一个二维格和两组不同的格基:X1
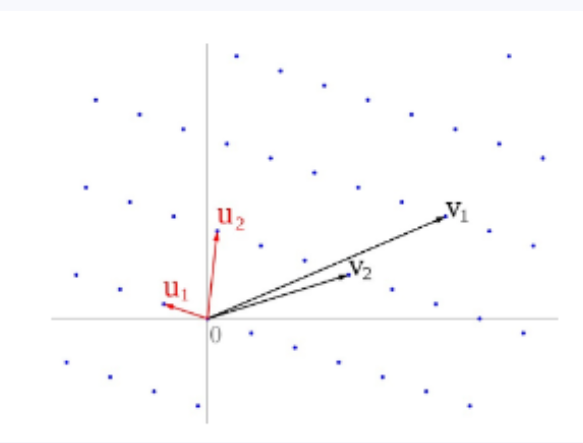
一个格的格基可以不是唯一的,例如,((2,1),(1,1))和((1,0),(0,1))都是二维整数格的一组格基。从上图中可以看到,即使是定义了同样的格的两组格基,其长度也可能相差很大。数学家和密码学家们普遍认为,对于一个维数足够高的格,通过一组随机选取的格基找到一组短格基,或得到一组线性无关的短格向量是困难的。这个问题称作最短独立向量问题(SIVP)。除此之外,还有一些其他的基于格的困难问题,如gap-SVP、BDD等。以上的困难问题通常属于数学上的理论研究范畴。在密码学的实际应用当中,格密码算法所基于的困难问题更多采用容错学习(LWE)问题。
LWE问题这样表述:给定随机矩阵A和向量As+e mod q,其中e是小的误差项,q是模数(通常取较大的素数),从中恢复随机的s是困难的。我们称(A,b=As+e mod q)为LWE样本,s为LWE秘密。容易看到,如果不存在误差项e,这一问题即为求解线性方程组,是易解的。然而,当引入误差e之后,LWE问题可归约到SIVP等格上的困难问题,即求解LWE问题的难度不低于求解格上的困难问题。
在应用于密码算法时,LWE问题存在一个很大的优势:存在“最坏情况到平均情况的归约”,即求解平均情况下的LWE问题,其难度不低于最难的SIVP问题实例。在一些早期的公钥密码算法,如基于背包问题的密码体制中,由于存在一些易解的背包问题实例,使得当参数选取不恰当时,密码算法的安全性易受攻击。而对于基于LWE问题的格密码来说,由于存在最坏情况到平均情况的归约,因而可以避免这种攻击的产生。这为基于LWE问题设计的密码算法带来了很大安全性上的优势。
直接通过LWE问题构造的密码学方案效率并不是很高。更多的时候,我们将整数向量用多项式代替,得到多项式LWE或称环LWE。一个环LWE样本为(a,b=as+e mod q),其中a,s,e 均为多项式。环LWE的安全性建立在理想格中相应数学问题困难性的基础之上。尽管这些问题在困难性上面被认为不如格问题更可靠,但目前还没有发现可以有效求解这些问题的算法。此外,还有可靠性介于LWE和环LWE问题之间的模LWE问题,以及这些问题的变种LWR、环LWR、模LWR问题。格密码的安全性基本上都依赖于这些问题的困难性。
1.1 基于格的公钥加密算法
通常,在一个基于LWE问题设计的密码算法中,我们将LWE样本作为公钥使用,而将LWE秘密作为私钥使用,这保证了公钥不会泄露关于私钥的信息。我们令公钥为 (a,b=as+e mod q),私钥为 s ,这里 a,b,s,e均为多项式,且s,e的系数相比于q是较小的(理论上s和e的系数应取为离散正态分布,但在实际应用中,出于实现上的效率和安全,s和e通常使用二项分布或均匀分布来模拟)。我们下面描述最基础的格公钥加密方案。
对于需要加密的消息,我们将消息记为 0-1 系数的多项式 m 。
(1)首先随机选取系数较小的多项式 r,e1,e2
(2)计算密文c=ar+e1 mod q和 d=br+e2+m(q-1)/2 mod q
容易看到,由于 as≈b mod q,故ars≈br mod q,且 (ar+e1)s≈br+e2 mod q。当s,e,r,e1,e2均足够小时,可以保证br+e2-(ar+e1)s mod q的系数均不超过(q-1)/4。故d-cs和m(q-1)/2的每个系数之差都不超过(q-1)/4。我们可以通过这样的方式从d-cs中还原m;若d-cs的第i个系数距离0更近,则令m的第i位为0;若 d-cs的第i位系数距离(q-1)/2更近,则令m的第i位系数为1。这样我们成功通过私钥s解密了密文(c,d),得到消息m。这一算法的安全性由两个部分保证:其一是私钥的安全性,由于公钥为LWE样本,通过公钥不会泄露私钥的信息;其二是消息的安全性,由于密文同样为LWE样本,通过密文在未知私钥的前提下,不会泄露消息。以上描述的简单方案是选择明文安全,而非选择密文安全的。对于具体的方案,则需要应用密码学中著名的Fujisaka-Okamoto变换,将以上的基础方案转变为选择密文安全的方案。
1.2 基于格的数字签名算法
对于RSA、椭圆曲线等密码体制来说,其中的公钥加密和数字签名算法存在一定的对偶性:可通过简单的交换公私钥,将公钥加密算法转化为数字签名算法。
然而,对于格密码而言,这种对偶性并不存在,这意味着我们需要通过新的方式构造数字签名算法。被密码学家广泛采用的一种方式,即通过零知识证明协议构造数字签名。零知识证明可能是密码学中最为神奇的一类应用。零知识证明解决这样一个问题:我们是否可以向他人提供对一个命题的证明,但却不泄露证明这一命题所需要的知识?尽管看起来有些反直觉,但这一点事实上是可以做到的。实现安全的数字签名,最基本的需求是令验证者有能力对签名者的身份进行认证。而这等价于这样的一个零知识证明:证明者可证明自己拥有(和对应身份的公钥匹配的)私钥,但不向验证者泄露关于私钥的信息。这是一类最简单的零知识证明协议,通常称为∑协议。
∑协议由以下三个步骤构成:
(1)证明者给出承诺w。证明者首先随机选择y,并通过y生成承诺w,交给验证者。
(2)验证者提出挑战 c。验证者给出均匀随机的挑战c。
(3)证明者给出应答z。证明者通过第一步中的y、挑战c以及用户私钥,得到应答 z。(我们额外要求z在其值域上是均匀随机的)验证者可通过用户公钥、挑战c以及承诺w确认z是否是由证明者合法生成的。
我们将(w,c,z)三元组称为协议的抄本(transcript)。在具备零知识性的 ∑ 协议中,我们通常要求在未知私钥的情况下(1) 通过w和c得到z是困难的;(2) 通过c和z得到w是容易的。因此,即使在未知私钥的前提下,(w,c,z)三元组也可以通过这样的方式生成:首先随机选取c和z,然后得到w。由于这一生成方式不需要私钥的参与,故协议的抄本不包含关于私钥的任何知识!这就保证了协议的零知识性。
由于∑协议需要证明者和验证者之间实施交互,故无法直接应用于构造数字签名。但注意到∑协议要求挑战c均匀随机选取,而正如我们所知,一个安全的哈希函数,其输出和随机值是不可区分的。因此,我们可以将承诺w和需要签名的消息m输入哈希函数H,并用哈希函数的输出模拟挑战 c,从而不需要额外的验证者提出挑战。与此同时,由于有签名消息的参与,也实现了消息和∑协议抄本的绑定。这个方法称为Fiat-Shamir变换。可以证明,安全的∑协议通过Fiat-Shamir变换,得到安全的数字签名方案。
下面我们简单介绍如何基于LWE问题构造∑协议,进而构造数字签名。和公钥加密算法类似,我们令公钥为 (a,b=as+e mod q),私钥为 s 。
(1)首先随机选取较小的y
(2)令承诺w为ay的高比特位,以排除误差项的影响
(3)对于挑战c,令应答z = y + cs。(注意到我们要求z均匀随机,故需要排除一些令z不随机的边缘取值:当z为边缘取值时,需要重新选取y并再次计算z。我们这里不展开细节)
由于ay = az – cas ≈ az – cb mod q,故只需验证w 是否为 az–cb的高比特位即可。对于需要签名的消息m和杂凑函数H,我们令c = H(w||m),即可将这一协议转化为签名算法(在验签时需要验证c = H(w||m))。
 电子发烧友App
电子发烧友App

























评论