电源设备中常用的四种变换电路（续）

电源设备中常用的四种变换电路（续）
Common Four Change Circuits in Power Supply Equipments

(上接总第11期)

3 DC/DC变换

将一种直流电压变换成另一种（固定或可调的）直流电压称为DC/DC变换（亦称直流变换器）。这种技术被广泛地应用于无轨电车、地铁列车、蓄电池供电的机动车辆的无级变速中，从而获得平稳地加速、减速、快速响应的性能，80年代兴起的电动汽车就是一例。

下面介绍利用自关断器件构成的典型DC/DC变换电路。

最基本的斩波电路如图形3.1所示，斩波器负载为R，当开关S合上时，uo=uR=Ud,并持续t1时间。当开关切断时uo=uR=0,并持续t2时间，T=t1＋t2为斩波器的工作周期，斩波器的输出波形见图3.1(b)。若定义斩波器的占空比D=t1/T,则从波形图可以获得输出电压平均值为

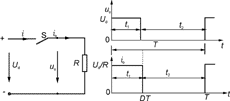
图3.1降压斩波电路原理
（a）电路(b)波形

若忽略开关的损耗，则输入功率Pi应与输出功率相

等，即从直流电源侧看的等效电阻Ri为

Ri=Ud/Ioa=Ud/(DUd/R)=R/D(3.3)

由式3.1可知，当占空比D从零变到1时，输出电压平均值从零变到Ud，其等效电阻也随着D而变化。

t1为斩波器导通时间，T为通断周期，通常斩波器的工作方式有两种：

（1）脉宽调制工作方式：维持T不变，改变t1。

（2）脉频调制工作方式：维持t1不变，改变T。

普遍采用的是脉宽调制方式。因为频率调制方式，容易产生谐波干扰，而且滤波器设计也比较困难。

3.1降压式（Buck）变换器

图3.1所示的直流变换器在使用时输出纹波较大，为降低输出纹波，在输出端接入电感L、电容C滤波电容，如图3.2（a）所示，图中V2为续流二极管。这就是降压（Buck）式变换器，其输出电压平均值Uo总是小于输入电压Ud。通过电感中的电流（iL）是否连续，取决于开关频率、滤波电感L和电容C的数值。

图3.2降压式（Buck）变换器
（a）电路(b)波形

当电路工作频率较高，若电感和电容量足够大并为理想元件，电路进入稳态后，可以认为输出电压为常数。当晶体管V1导通时，电感中电流呈线性上升，因而

Ud－Uoa=L(iomax－iomin)/ton=L△ion/ton

式中ton是晶体管导通时间。

当晶体管截止时，电感中电流不能突变，电感上感应电动势使二极管导通，这时

Uoa=L(iomax－iomin)/toff=L△ioff/toff

式中toff为晶体管截止时间。在稳态时△ion=△ioff=△i。

因为电感滤波保持了直流分量，消除了谐波分量。输出电流平均值为

Ioa=(iomax＋iomin)/2=Uoa/RL(3.4)

3.2升压式（Boost）变换器

图3.3为升压式变换器，它由功率晶体管V1、储能电感L、二极管V2及滤波电容C组成。当晶体管导通时，电源向电感储能，电感电流增加，感应电动势为左正右负，负载Z由电容C供电。当V1截止时，电感电流减小，感应电动势为左负右正，电感中能量释放，与输入电压顺极性一起经二极管向负载供电，并同时向电容充电。这样把低压直流变换成高压直流。其输出电压平均值将超过电源电压Ud其电路的工作波形如图3.3(c)所示。

在电感电流连续的条件下，电路工作于图3.3（b）所示的两种状态。

图3.3升压式(Boost)电路
(a)电路；(b)等效电路；（c）波形

图3.4升/降压式电路
(a)电路；(b)等效电路；(c)波形

（1）当晶体管导通、二极管截止（即0≤t≤t1=DT）期间，t1=0～DT，t=0时刻，V1导通，电感中的电流按直线规律上升

Ud=L(I2－I1)t1=L△I/t1(3.5)

（2）当晶体管由导通变为截止（即t1≤t≤T）期间，电感电流不能突变，产生感应电动势迫使二极管导通，此时

Uoa－Ud=LI/t2,t2=DT～T=(1－D)T

则△I=Udt1/L=(Uoa－Ud)t2/L

将t1=DT,t2=(1－D)T代入上式，则求得

Uoa=Ud/(1－D)(3.6)

式3.6表明，BoostDC/DC变换器是一个升压斩波器。当D从零趋近于1时，Uoa从Ud变到任意大。同理可求得输入电流

I=Ioa/(1－D)(3.7)

T=△ILUo/Ud(Uoa－Ud)(3.8)

△I=Ud(Uoa－Ud)/fLUoa=UdD/fL(3.9)

式中f为开关转换频率。若忽略负载电流脉动，那么[0,t1]期间，电容上泄放的电荷量，反映了电容峰—峰电压脉动量，亦即输出电压uo的脉动量(3.10)

由式3.5和式3.9求得t1=(Uoa－Ud)/Uoaf,并代入式3.10得，见图3.3（c）

△Uc=Ioa(Uoa－Ud)/UoafC=IoaK/fC,

K=(Uoa－Ud)/Uoa(3.11)

3.3升/降压式（Buck－Boost）变换器

图3.4（a）为Buck－Boost电路，这是降压－升压混合电路，其输出电压可以小于输入电压Ud，也可以大于输入电压，而输出电压极性与输入电压相反。其工作波形示于图3.4(c)。

在电感电流iL连续条件下，Buck－Boost电路工作于图3.4(b)所示的两种状态。

经分析推导，可以得出输出电压平均值为

Uoa=－UdD/(1－D)(3.12)

同前面分析一样，可得

Io=IoaD/(1－D)(3.13)

4AC/AC变换

　　在需要不同于市电频率或频率可变的交流电源的场合，通常采用AC/AC变换电路。

4．1AC/AC变换的基本原理

图4.1（a）所示为AC/AC变换器的原理电路图。实际上是由正组（P）双半波变流器和负组（N）双半波变流器反并联组成的。正组由V1和V2组成，负组由V3和V4组成。

当正组工作时，分别触发V1和V2使之导通，负载上获得正向电压。而负组工作时，对V3和V4触发使之导通，负载上获得反向电压。现以电阻性负载为例，并假定两组变流器不同时工作。

（1）整半周工作方式

假定输出交流电压的频率(fo)为电源频率（fs）的1/3，即To=3Ts。为此在输出的前半周期内（To/2）,让正组变流器工作3个电源电压整半周，在此期间内负组变流器被封锁；然后在输出的后半周期内，让负组变流器导通3个电源整半周，在此期间内正组变流器停止工作，这样可以获得如图4.1（b）所示的波形，其输出电压中的基波分量的频率为电源频率的1/3，即fo=fs/3，以此类推。

按整半周工作方式，输出频率是不能连续可调的，而且输出电压中包含大量的谐波。

（2）α调制工作方式

若每个电源半周期不是整半周期导通，而是控制α不同，让输出电压按理想的正弦进行调制，则能获得如图4.1（c）所示的波形，其输出电压中的基波频率仍然为电源频率的1/3，但其输出波形，比图4.1(b)更接近正弦波，其谐波含量降低。这种工作方式是实际AC/AC变换器所采用的。

（3）高频工作方式

这种工作方式不同于前述的两种，在1个电源电压的半周期内，两组变流器要轮流工作多次，当图4.1(a)的晶闸管用自关断器件代替时，就可以实现这种工作方式，而且要求先封锁已导通的变流器，然后才能使另一组变流器投入工作。若在1个电源电压周期里，以高速率切换两组变流器，使其轮流工作，则能获得如图4.1（d）所示的波形，并称它为高频工作方式。

图4.1AC/AC变换原理电路
（a）电路；(b)整半周方式；
(c)α调制方式；(d)高频方式

4.2α调制工作方式的实现

　　现以单相—单相直接变频电路为例说明α调制工作方式的原理及其实现方法。图4.2为单相桥式AC/AC变换电路。为了在负载一获得交变电压，可以交替地让正组变流器和负组变流器轮流工作，并控制α的大小，使得输出电压的平均值按正弦规律变化。在半周期内，先让控制角α由大变小，再由小变大，则输出电压的平均值将按低频正弦的规律变化。

设理想的输出电压为(4.1)

变流器输出电压平均值的基本公式为

uo=(pUm/π)sin（π/p）cosα(4.2)

式中p为脉波个数。变流器输出电压同触发角α之间符合余弦函数关系。图4.2(a),p=2,sin（π/2）=1,则uo=(2Um/π)cosα，将所希望的输出电压波形ur=Ursinω0t同us=（2Um/π）cosωst进行比较，从而求得对应输出电压每瞬时的触发角大小，如图4.2（b）所示的那样，该图对应电阻性负载，两组变流器均工作于整流方式。

为了保证两组中的晶闸管不同时导通，两组之间切换时要留有一定的间隙时间to（大于器件的关断时间），在这期间，两组均不工作。

图4.2α调制工作方式原理
（a）电路；(b)波形

图4.3三相半波/单相
负载AC/AC变换电路

图4.4电阻负载时的电压波形图

4．3AC/AC变换器典型电路

　　以三相—单相直接变频电路供给阻性负载为例，图4.3所示为由两组三相半波变流器构成的AC/AC变换器。通常对于电源是市电的AC/AC变换器的输出频率限于电源频率的1/3以下，因为过高的输出频率将带来谐波增加的弊病。改变基准正弦波的频率，就可以改变输出频率。图4.4给出了负载输出电压的波形。

有关AC/AC变换器的内容，多在变频技术中应用，请读者参阅有关专著。