滤波电路的设计 - 电源滤波设计关键基础精华集锦

　　三、滤波电路的设计

　　滤波电路的设计

　　交流电经过二极管整流之后，方向单一了，但是大小（电流强度）还是处在不断地变化之中。这种脉动直流一般是不能直接用来给无线电装供电的。要把脉动直流变成波形平滑的直流，还需要再做一番“填平取齐”的工作，这便是滤波。换句话说，滤波的任务，就是把整流器输出电压中的波动成分尽可能地减小，改造成接近恒稳的直流电。

　　电容滤波

　　电容器是一个储存电能的仓库。在电路中，当有电压加到电容器两端的时候，便对电容器充电，把电能储存在电容器中；当外加电压失去（或降低）之后，电容器将把储存的电能再放出来。充电的时候，电容器两端的电压逐渐升高，直到接近充电电压；放电的时候，电容器两端的电压逐渐降低，直到完全消失。电容器的容量越

　　大，负载电阻值越大，充电和放电所需要的时间越长。这种电容带两端电压不能突变的特性，正好可以用来承担滤波的任务。

　　图5-9是最简单的电容滤波电路，电容器与负载电阻并联，接在整流器后面，下面以图5-9（a）所示半波整施情况说明电容滤波的工作过程。在二极管导通期间，e2 向负载电阻Rfz 提供电流的同时，向电容器C充电，一直充到最大值。e2 达到最大值以后逐渐下降；而电容器两端电压不能突然变化，仍然保持较高电压。这时，D 受反向电压，不能导通，于是Uc便通过负载电阻Rfz 放电。由于C和Rfz 较大，放电速度很慢，在e2 下降期间里，电容器C上的电压降得不多。当e2 下一个周期来到并升高到大于Uc时，又再次对电容器充电。如此重复，电容器C两端（即负载电阻Rfz ：两端）便保持了一个较平稳的电压，在波形图上呈现出比较平滑的波形。图5-10（a）（b）中分别示出半波整流和全波整流时电容滤波前后的输出波形。

　　显然，电容量越大，滤波效果越好，输出波形越趋于平滑，输出电压也越高。但是，电容量达到一定值以后，再加大电容量对提高滤波效果已无明显作用。通常应根据负载电用和输出电说的大小选择最佳电容量。表5-2 中所列滤波电容器容量和输出电流的关系，可供参考。 电容器的耐压值一般取 的1．5倍。

　　表5-3中列出带有滤波器的整流电路中各电压的关系。 表一、

　　输出电流2A左右1A左右0.5-1A左右0.1-0.5A100-50mA50mA以下

　　滤波电容4000u2000u1000u500u200u-500u200u

　　采用电容滤波的整流电路，输出电压随时出电流变化较大，这对于变化负载（如乙类推挽电路）来说是很不利的。

　　二、电感滤波

　　利用电感对交流阻抗大而对直流用抗小的特点，可以用带铁芯的线圈做成滤波器。电磁滤波输出电压较低，相输出电压波动小，随负载变化也很小，适用于负载电流较大的场合。

　　三、复式滤波器。

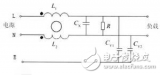
　　把电容按在负载并联支路，把电感或电阻接在串联支路，可以组成复式滤波器，达到更佳的滤波效果口这种电路的形状很象字母π，所以又叫π型滤波器。

　　图5－12所示是由电磁与电容组成的LC滤波器，其滤波效能很高，几乎没有直流电压损失，适用于负载电流较大、要求纹波很小的场合。但是，这种滤波器由于电感体积和重量大（高频时可减小），比较笨重，成本也较高，一般情况下使用得不多。

　　由电阻与电容组成的RC滤波器示于图5－13中。这种复式滤波器结构简单，能兼起降压、限流作用，滤波效能也较高，是最后用的一种滤波器。上述两种复式滤波器，由于接有电容，带负载能力都较差。

　　四、RC滤波电路的计算及公式

　　RC滤波电路的计算及公式

　　对于无源RC一阶低通滤波电路，其传递函数为G（s）=1/（RCs+1）。转换为信号经过它的衰减的计算方法为：

　　Uo=Ui/［（2*Pi*f*R*C）^2+1］^0.5

　　式中：Uo为输出电压；Ui为输入电压；Pi为圆周率；f为信号频率。

　　对于无源RC二阶（以上）低通滤波电路，由于此处用文字行不大好表达，所以就不写出了。

　　五、电容滤波电路

　　滤波电路

　　整流电路虽然可将交流电变成直流电，但其脉动成分较大，在一些要求直流电平滑的场合是不适用的，需加上滤波电路，以减小整流后直流电中的脉动成分。

　　一般直流电中的脉动成分的大小用脉动系数来表示：

　　脉动系数（S）＝ 　　　GS0712

　　例如，全波整流输出电压uL可用付氏级数展开为：

　　 　　　 GS0713

　　其中基波最大值为0.6U2，直流分量（平均值）为0.9 U2，故脉动系数S≈0.67 。同理可求得半波整流输出电压的脉动系数为S＝1.57，可见其脉动系数是比较大的。一般电子设备所需直流电源的脉动系数小于0.01，故整流输出的电压必须采取一定的措施，一方面尽量降低输出电压中的脉动成分，另一方面尽量保存输出电压中的直流成分，使输出电压接近于较理想的直流电源的输出电压。这一措施就是滤波。

　　最基本的滤波元件是电感、电容。其滤波原理是：利用这些电抗元件在整流二极管导通期间储存能量、在截止期间释放能量的作用，使输出电压变得比较平滑；或从另一角度来看，电容、电感对交、直流成分反映出来的阻抗不同，把它们合理地安排在电路中，即可达到降低交流成分而保留直流成分的目的，体现出滤波作用。

　　常用的滤波电路有无源滤波和有源滤波两大类。其中无源滤波的主要形式有电容滤波，电感滤波和复式滤波（包括倒L型LC滤波，π型LC滤波和π型RC滤波等）。有源滤波的主要形式是有源RC滤波。

　　电容滤波

　　半波整流电容滤波电路如图Z0710所示。其滤波原理如下：

　　电容C并联于负载 RL的两端，uL＝uC。在没有并入电容C之前，整流二极管在u2的正半周导通，负半周截止，输出电压uL的波形如图中红线所示。并入电容之后，设在 ωt=0时接通电源，则当u2由零逐渐增大时，二极管D导通，除有一电流iL流向负载以外还有一电流iC向电容C充电，充电电压uC的极性为上正下负。如忽略二极管的内阻，则uC 可充到接近u2的峰值u2m。在u2 达到最大值以后开始下降，此时电容器上的电压uc也将由于放电而逐渐下降。当u2＜uc时，D因反偏而截止，于是C以一定的时间常数通过RL 按指数规律放电，uc下降。直到下一个正半周，当u2 ＞uc时，D又导通。如此下去，使输出电压的波形如图中蓝线所示。显然比未并电容C前平滑多了。

　　全波或桥式整流电容滤波的原理与半波整波电容滤波基本相同，滤波波形如图Z0711 所示。

　　从以上分析可以看出：

　　1. 加了电容滤波之后，输出电压的直流成分提高了，而脉动成分降低了。这都是由于电容的储能作用造成的。电容在二极管导通时充电（储能），截止时放电（将能量释放给负载），不但使输出电压的平均值增大，而且使其变得比较平滑了。

　　2．电容的放电时间常数（τ＝RLC）愈大，放电愈慢，输出电压愈高，脉动成分也愈少，即滤波效果愈好。故一般C取值较大，RL也要求较大。实际中常按下式来选取C的值：

　　RLC≥（3～5＞T（半波） GS0714

　　RLC≥（3～5）T／2（全波、桥式） GS0715

　　3．电容滤波电路中整流二极管的导电时间缩短了，即导通角小于180°。而且，放电时间常数越大，导通角越小。因此，整流二极管流过的是一个很大的冲击电流，对管子的寿命不利，选择二极管时，必须留有较大余量。

　　 4. 电容滤波电路的外特性（指UL与IL之间的关系）和脉动特性（指S与IL 之间的关系）比较差，如图Z0712 所示。可以看出输出电压UL和脉动系数S随着输出电流IL 的变化而变化。当IL＝0（即RL= ∞ ）时，UL = U2（电容充电到最大值后不再放电），S = 0。当IL增大（即RL减小）时，由于电容放电程度加快而使UL下降，UL 的变化范围在 U2 ～0.9 U2之间（指全波或桥式），S变大。所以，电容滤波一般适用于负载电流变化不大的场合。

　　5．电容滤波电路输出电压的佑算。如果电容滤波电路的放电时间常数按式GS0714或GS0715 取值的话，则输出电压分别为：

　　UL＝（0.9～1.0）U2 （半波） GS0716

　　UL＝（1.1～1.2）U2 （全波） GS0717

　　电容滤波电路结构简单、使用方便、应用较广。