1-1 电路及电路模型
电源:电源元件、受控电源
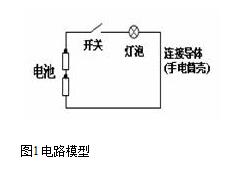
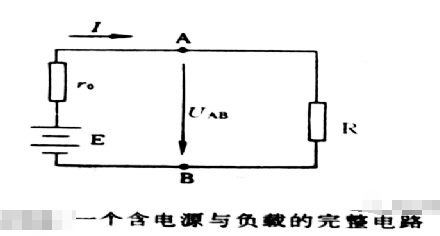
构成电路的三个环节:电源、负载以及连接两个环节的中间环节即导线
电路:电流流通的路径
电路理论是建立在模拟概念的基础上,即用理想化的模型来描述实际电路,电路模型指理想元件组成的电路图
注意:
一个器件的电路模型及参数与该器件的工作条件有关;
电路模型是一种数学模型;理想元件:具有精确的数学运算关系的电路元件。
如R(电阻)、L(电感)、C(电容)等;
电路模型只是对实际物理过程的一种近似描述;模型的繁简与实际工程计算要求的精度有关;
1-2 电流、电压和功率
电流、电流强度、电压、功率定义和计算
电位也称电势
电流的参考方向:假设的电流正方向
电压的参考方向:假设的电压正方向
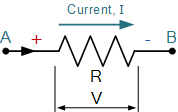
关联参考方向:如果电流从标以“+”号的端点注入,并从标以“-”号的端点流出,则电流的参考方向与电压的参考方向一致,称为关联参考方向。
在电压、电流取关联参考方向下,p=ui表示该元件“消耗”(吸收)的电功率大小,非关联参考方向下,p=-ui表示该元件是“供出”功率大小
在分析电路时,无需考虑电流电压的实际方向,只需在图中标定参考方向,最终计算结果的正、负就反映了实际方向。参考方向一经选定就不能再变动。
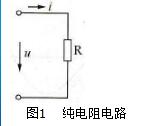
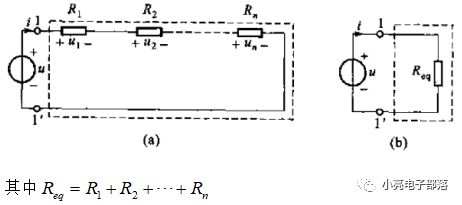
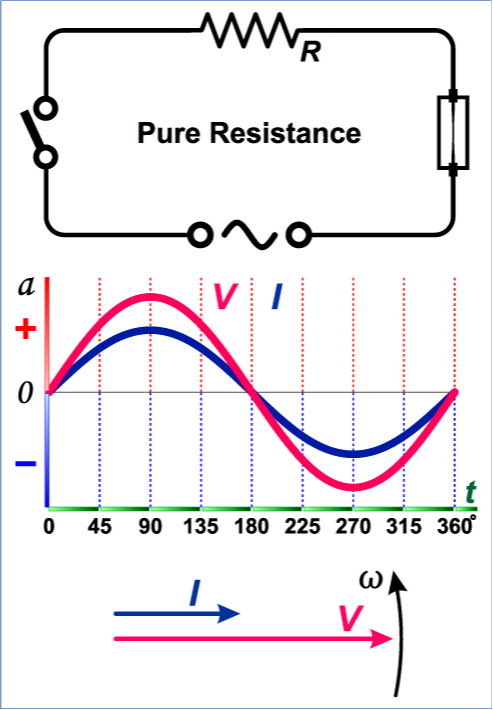
1-3 电阻元件

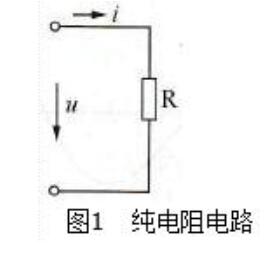
如果一个二端元件在任意时刻t,其电压与电流的关系(伏安关系,VAR)服从欧
姆定律,即:u=R i,则该元件称线性二端电阻元件。
另一个表征电阻元件伏安关系的一个参数为G(Conductance)电导,单位:西门子(S)二者关系:R=1/G
并联的电阻是电导相加
电阻是吸收功率
判断元件是吸收功率还是提供功率
欧姆定律是定义在电阻上的电压、电流取关联参考方向下的。u= R i
若为非关联参考方向,则u = - R i
P = ui(关联参考方向) 或 P = -ui(非关联参考方向)
在较为简单的电路模型中的一个判断方法是,如果实际电流方向和实际电压方向一致,那么元件消耗功率,否则元件供出功率
电容存储的电场能量只和端电压有关,因为电容元件端电压不能跃变,所以电容上的能量也不能跃变

1-5 电感元件
电感元件的Ψ-i关系,u-i关系,功率和能量关系
一个二端元件,如果在任意时刻t它的磁链Ψ与它的电流i之间关系,满足方程: Ψ =L i则该元件称为线性电感元件。式中L为常数,单位为享利(H)。
任意时刻t电感上的电流与电感的历史情况有关,对电压具有记忆能力
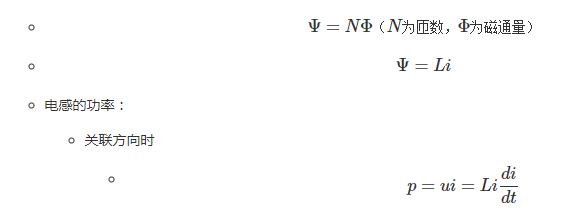
上式表明:
当di/dt = 0,u,p=0,电感上的能量不变
当di/dt>0,p>0,电感将储存能量
当di/dt<0,p<0,电感将释放能量
电感元件在某一时刻所储存的磁场能量只与该时刻电流(或磁链)的瞬时值有关,因为电感中的电流不能跃变。所以电感上的能量不能跃变。
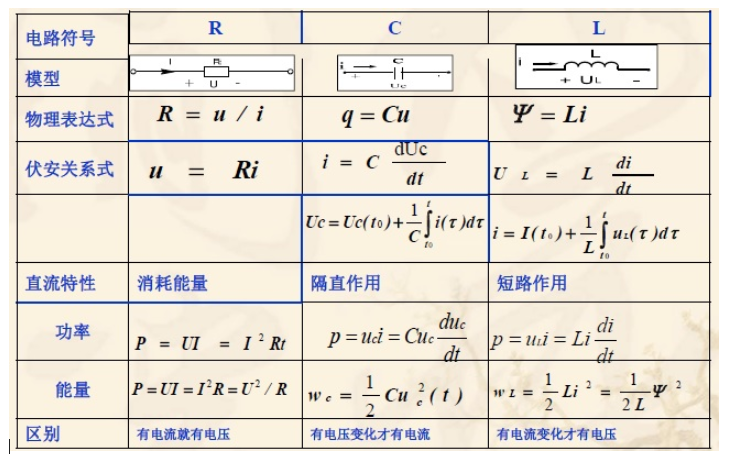
1-6 电压源和电流源
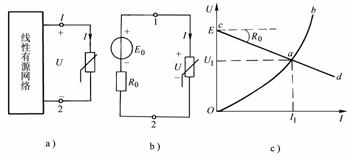
电压源:如果一个二端元件接到任一电路后其两端电压us(t)总能保持规定值,与通过它的电流大小无关,则该二端元件就称为电压源。
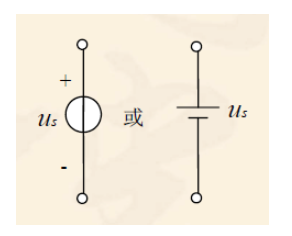
说明:
理想电压源两端的电压与外电路无关,而通过它的电流的大小和方向,则需要电压源和外电路共同确定。
电压源的电压、电流习惯上采用非关联参考方向。在这种情况下,p=ui 代表电压源向外电路提供功率。
理想电压源在实际中不存在。
电流源:如果一个二端元件接到任一电路后,该元件能够对外电路提供规定的电流is(t),无论其两端电压大小如何,则该二端元件就称为电流源
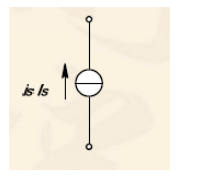
1-7 受控源
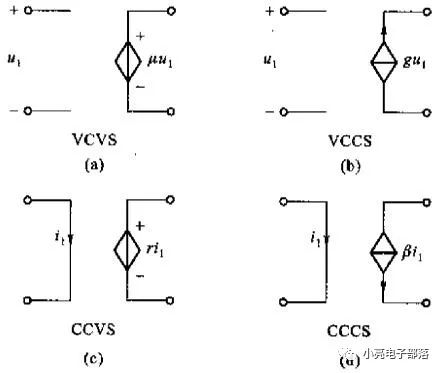
受控电源是一个具有两条支路的双端口元件,其输出端口的电压(或电流)受控于输入端口的电压(或电流)。
可以分成四类:
- 电压控制电压源
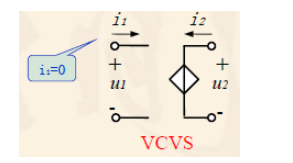
菱形表示受别的支路控制
- 电压控制电流源
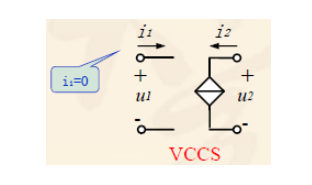
- 电流控制电压源
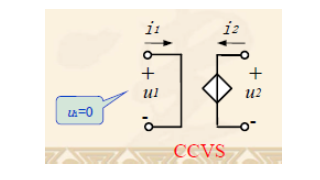
- 电流控制电流源
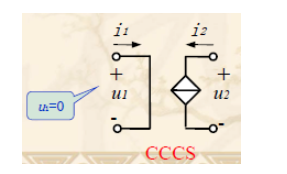

受控于电流,电压为0;受控于电压,电流为0
说明:
对理想受控电源
当控制变量为电压时,控制回路是开路的,如:VCVS,VCCS;
当控制变量为电流时,控制回路是短路的,如:CCVS,CCCS;
对于控制回路(输入回路),因为p2=u2i2=0,故输入端的功率为零;
对于被控制回路(输出回路),因为p2=u2i2≠0,表明输出功率不为零,故受控源为一种有源元件。
受控源与独立源在电路中的作用:独立电源是激励,表示其对其它电路的一种作用;受控电源表示控制回路与被控制回路之间的一种耦合关系。
只要电路中有一条支路的电压(或电流)受到另外任意一条支路电压(或电流)控制时,它们就构成了一个受控电源。
1-8 基尔霍夫电流定理(KCL)
电路的基本规律包含两方面的内容(即两大类约束关系):
其一:电路中的各种元件本身具有的约束关系—元件的伏安关系(个体、欧姆定律);
其二:电路的结构整体所遵循的约束关系—结构约束(整体、基尔霍夫定理)。
支路、节点、回路、网孔的概念
基尔霍夫定理:
在集总参数电路中,任意时刻, 流入任一节点的电流之和等于流出该节点的电流之和:

集总参数元件、电路的概念
对于集总参数电路,由基尔霍夫定律唯一地确定了结构约束(又称拓扑约束,即元件间的联接关系决定电压和电流必须遵循的一类关系)
KCL适用于任何集总参数的电路,与电路元件的性质无关,揭示了在每一节点上的电荷的守恒;*KCL给一节点上各支路电流之间加上了线性约束:
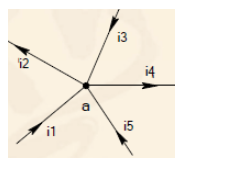
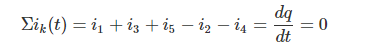
使用:
把KCL应用到某一节点时,首先要指定每一支路的电流参考方向;
应用KCL时,必须要和电流的两套符号打交道,即:
列KCL方程时,有关支路电流前的正负号选择;
各支路电流取值的正负号选择;
推广应用:
KCL对于一个封闭面(常称为广义节点)也是适合的
在集总参数电路中,任一时刻流出(或流入)任意一个封闭面的电流代数和为零.
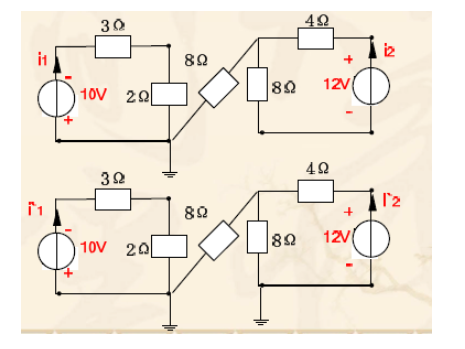
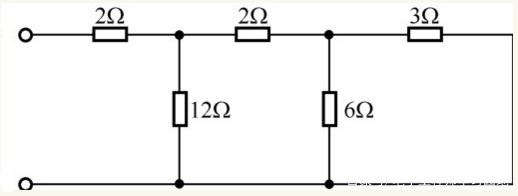
上图的中间8Ω的电阻上没有电流,如果有电流就不符合流入=流出了
而下图的中间8Ω的电阻上有电流,相当于和右边的8Ω电流并联,两个接地线之前的节点是等电位的,可以看作有一条导线相连,并联部分的电阻为4Ω,所以i1 = i1',i2 < i2'
注意:此图中的接地并非真正的“接地”,只是表名电位相等,对此图的理解可以是右侧回路的电流经过了中间的8Ω的电阻,然后进入地下,然后从右侧的接地处又流入右侧回路
1-9 基尔霍夫电压定理(KVL)
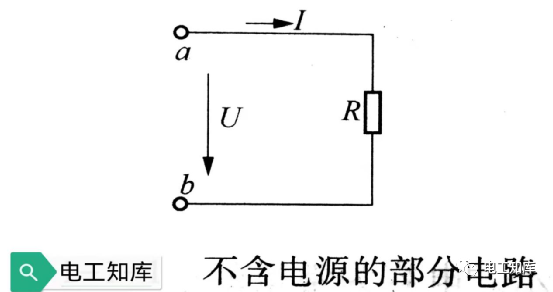
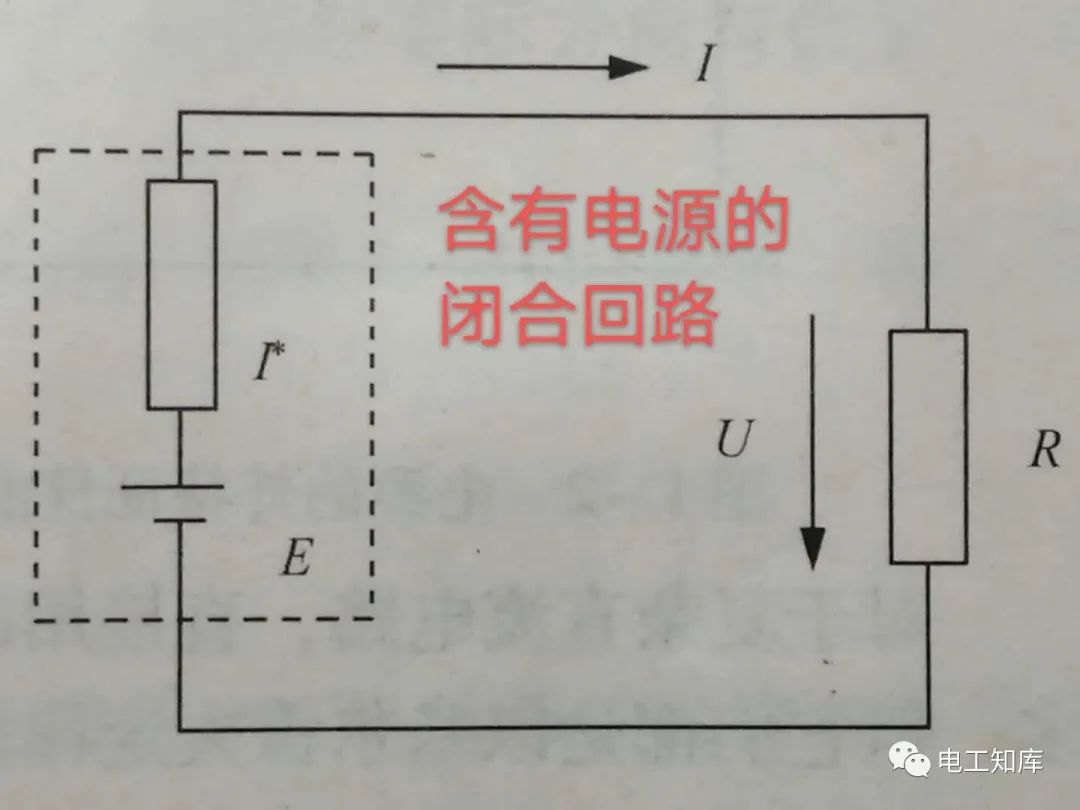
在集总参数电路中,任意时刻, 对任意回路,按一定方向巡行一周,回路中各支
路电压的代数和为零。
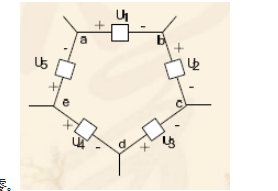
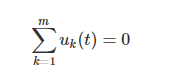
应用KVL时,若规定支路电压参考方向与巡行方向相同时取正,反之取负
使用:
应用KVL时,应首先要标定各支路的电压参考方向即网孔绕行方向
列KVL方程时,亦有两套符号的问题
KVL是能量守恒在集总参数电路中的具体反映;
KVL适用于任何集总参数电路,与电路元件的性质无关;
KVL回路中的各支路电压之间加上了线性约束
推广应用:
KVL即可以用于由导线连接的任何回路,也可以用于其他任何非闭合路径(即广义回路)
把电路中电位相同的点称为等电位点。对于两个等电位点可以对其短接或开路处理
 电子发烧友App
电子发烧友App












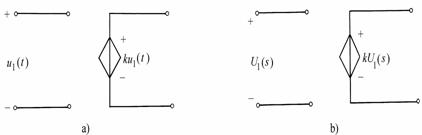
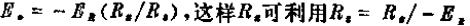
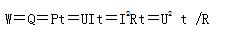
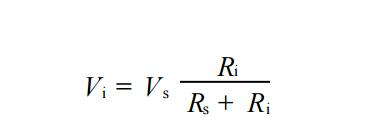










评论