在电子仿真中,元件值总是被认为是固定的。有时,设计人员想要更改这些值以尝试测试不同的电路行为。其他时候,有必要考虑这样一个事实,即相同的值可能会发生变化,因为并非每个电子元件都是理想的。市场上提供了许多相同电子元件的示例,但在给定容差内具有不同的值。让我们看看如何使用蒙特卡罗分析来模拟这些值的变化。
蒙特卡罗分析
此过程执行大量模拟,其中每个分量的值连续随机变化。他们试图遵循非常自然和随机的分布。
让我们从一个非常简单的例子开始
图 1中的图表显示了一个典型的 RC 电路,其中电容器充电的时间取决于时间常数。准确地说,RC秒后电压达到电源电压的63%左右。在这种情况下,电容器两端的电压正好在 1000 * 100E-6 秒后为 6.32 V。
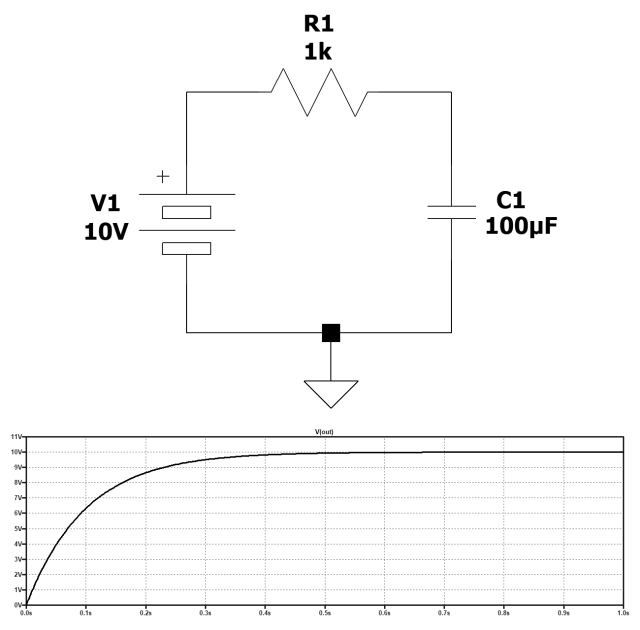
图 1:典型的 RC 电路
在这个示例方案中,我们假设所有组件的值都是理想的,即:
电源电压V1为10V;
电阻 R1 为 1000 欧姆;
电容器 C1 的容量为 100 微法拉。
由于所有组件都具有理想值,因此即使生成的图形也是理想的,并且没有考虑可能的异常或变化。市场提供具有 1%、5%、10% 等容差的电阻器。即使是电容器也可能具有与板数据不同的特性,其容差约为 20% 或更多。由于各种原因,电池电压可能会降低或升高。由于所有这些原因,设计人员需要获得一个“更真实”的图表,该图表考虑到所用组件值的真实变化,使仿真行为更接近真实系统的行为。这就是为什么我们真的希望组件的值不是理想的而是真实的,具有以下容差:
电池 V1:10 V,2% 容差;
电阻 R1:1000 欧姆,10% 容差;
电容器 C1:100 微法拉,容差为 25%。
这意味着,实际上,所使用的电子元件可以采用以下值范围:
电池 V1:电压在 9.8 V 和 10.2 之间;
电阻 R1:欧姆值在 900 到 1100 欧姆之间;
电容器 C1:容量在 75 微法拉和 125 微法拉之间。
这些变化显然是同时发生的。组合的可能值在理论上是无限的,但设计人员需要在容差提供的自然范围内观察具有尽可能多变化的电容器电荷图。功能:
mc(值,公差)
在 x * (1 + y) 和 x * (1-y) 之间随机生成一个随机值,在公差范围内指定,具有均匀分布。LTspice 接线图中包含的指南如下:
.param 电压 = mc (10.2 / 100)
.param 电阻 = mc (1000,10 / 100)
.param 电容 = mc (100u, 25/100)
.step 参数模拟 1 100 1
.meas TRAN V_Batt PARAM 电压
.meas TRAN R_Res PARAM 电阻
.meas TRAN C_Cap PARAM 电容
.meas TRAN RC PARAM 电阻 * 电容
该方案的模拟(如图2所示)) 执行一百次。它为每个组件生成一百个不同的值。建议仔细观察图表,组件的值和指令,以深入了解程序并能够继续阅读文章。正如您这次看到的,该图包括几条曲线,对应于电容器上增加的电压,具有一百个不同的组件值。进行的模拟越多,最终曲线就越逼真,请记住,模拟时间与执行的步数成正比。有时,如果电路极其复杂并且由许多组件组成,则模拟器需要很长时间来执行数学计算。
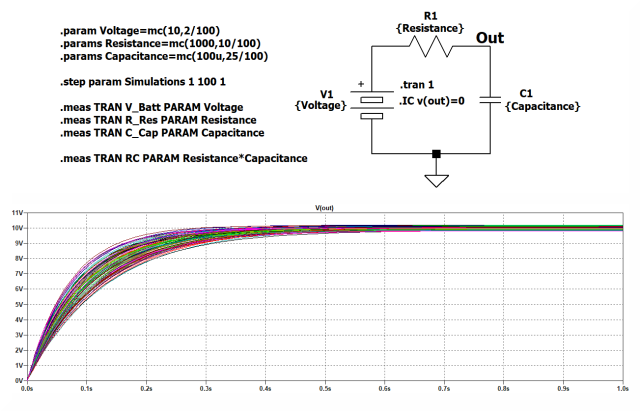
图 2:RC 电路的接线图以及蒙特卡罗模拟的指令和电容器上的电压图
在下表中,您将找到程序生成的数百个电压、电阻和容量的一些值。显然,这些是由软件生成的随机值,因此,对于进一步的模拟,它们总是不同的。
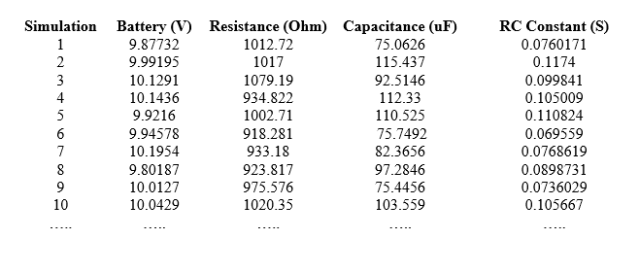
以下结果显示了随机生成量的最小值和最大值,参考了一百次模拟:
电池V1
产生的最小蒙特卡罗电压:9.80065 V
产生的最大蒙特卡罗电压:10.1999 V
电阻器R1
最小蒙特卡罗欧姆值:901.75 欧姆
最大蒙特卡罗欧姆值:1099.36 欧姆
电容C1
最小蒙特卡罗容量:75.0626 uF
最大蒙特卡罗容量:124,759 uF
时间常数RC
最小“t”:0.069559 秒
最大“t”:0.13325 秒
在图 3 中,我们可以看到电容器电压图表中发生的情况,恰好在 0.069559 秒和 0.13325 秒之间的时间间隔内,执行了一百次蒙特卡罗模拟。组件在不同环境中的变化使我们了解它们如何影响和修改电子电路的行为及其时序。
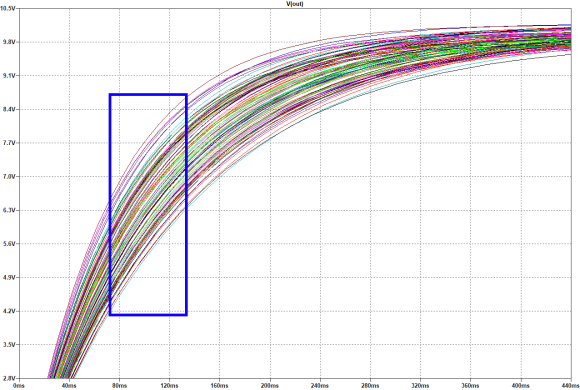
图 3:使用软件生成的组件值观察时间常数
使用 SiC 进行蒙特卡罗模拟
在 DC/DC 转换器中,最重要的功率损耗是由 ON 和 OFF 开关转换引起的。损耗与开关频率和寄生电容值成正比。用于开关的SiC MOSFET是最重要的,尤其是 Rds (ON) 参数和开关速度。图 4 中所示的升压转换器由以下组件组成:
一个 13 V 发电机 V1,可以是电池或光伏板;
一个 2 mH 电感器;
UF3C065080T3S 碳化硅MOSFET;
50 欧姆负载。
该升压转换器以开关频率 f = 10 kHz 运行。
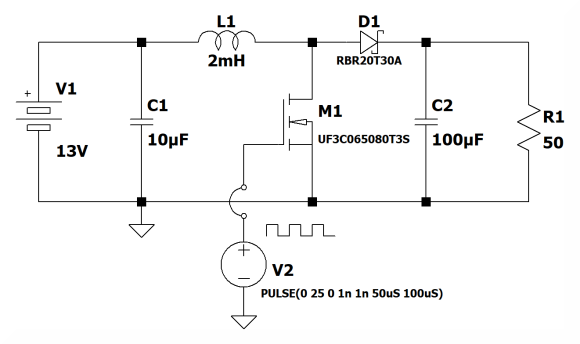
图 4:13V 至 26V DC/DC 升压转换器
这些组件不是真实的,因此我们可以很容易地承认以下容差:
V1:+/- 20%
C1:+/- 25%
L1:+/- 15%
C2:+/- 25%
R1:+/- 5%
温度:+/- 30%
图中包含的 SPICE 指令和命令如下:
.param 电压 = mc (13.20 / 100)
.param Cap1 = mc (10u, 25/100)
.param Induct = mc (2m, 15/100)
.param Cap2 = mc (100u, 25/100)
.param 负载 = mc (50.5 / 100)
.param T = mc (27.30 / 100)
.temp {T}
.step 参数模拟 1 10 1
.meas TRAN V_Batt PARAM 电压
.meas TRAN Capacitor1 PARAM Cap1
.meas TRAN 电感 PARAM 电感
.meas TRAN Capacitor2 PARAM Cap2
.meas TRAN 电阻参数负载
.meas TRAN 温度 PARAM T
对于简短但全面的模拟,我们仅提供了相应容差范围内的十个随机值。请记住,模拟次数越多,最终结果就越好。在图 5 中我们可以看到十种不同操作条件的模拟,持续了大约 15 分钟,并在 1.3 Gb 的硬盘上生成了一个临时文件。下表显示了蒙特卡罗方法生成的分量值,无论如何都在声明的容差范围内。
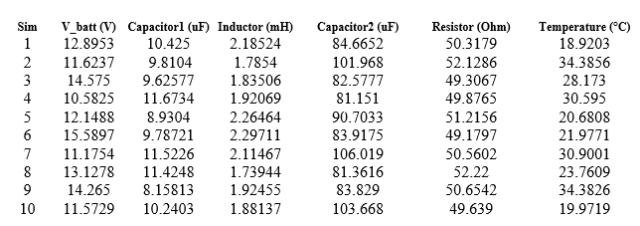
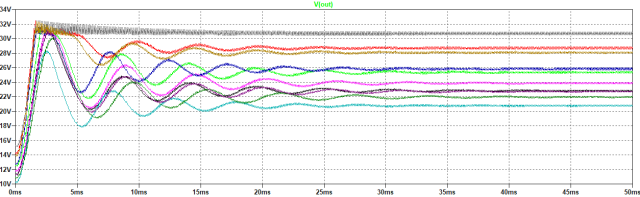
图 5:Boost 转换器行为的 Monte Carlo 模拟,它显示了负载上的电压取决于电子元件的不同值
结论
通过适当的操作,还可以随机改变其他参数,例如 Sic MOSFET 的 Rds (ON)、工作频率等。计算机电子模拟通常是完美且无错误的,尤其是在指定唯一且准确的值时。使用蒙特卡罗方法增加了测试的真实因素,从而使电路的行为更接近真实的行为。使用这种方法,可以在电子元件的值处于允许的最小值和最大值时观察系统的行为。
审核编辑:刘清
 电子发烧友App
电子发烧友App




























评论