三相变单相变压器问题探讨

一、“三相变单相”、“三相变二相”云云

虽然随着电力电子技术的飞速发展,这个问题的迫切性已逐渐被淡化.但如果有谁真能提出一个切实可行、满足上述两个条件的“三变单变压器”方案,仍然有相当的市场,仍然能成为轰动国内外变压器制造业的大事!

遗憾的是,没有.这个“没有”是指国内外相关专业杂志上未见刊登过. 但广告里有,或在BBS论坛里能找到哪位高手的相关声明. 对此,下面的话我就不说了.

为统一认识,这儿有必要插一下“平衡”与“对称”两个术语. “平衡”一词除了数学意义上的“方程式平衡”以外,在电工领域是能量、功率层面的术语.例如平衡变压器输出两端口的功率为使三相“对称”而保持的某种“平衡”;变压器中直接与功率传递相关的磁势平衡等.

三相系统的“对称”是指电压、电流、阻抗层面的术语.

若三相电网对称,符合以下特征,三相线电流才算“对称”:

1) 三相线电流的辐值或有效值相等;

2) 三个线电流的相位彼此相差120度;

3) 与产生它的三相线电压必需同相序.
至于构成对称电网的电压(势),除上述1、2外,还应符合“顺相序”要求.

二、“三变单系统”种种

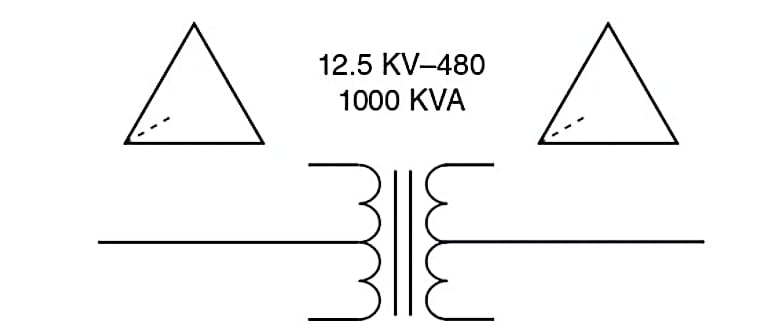
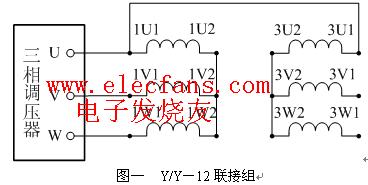
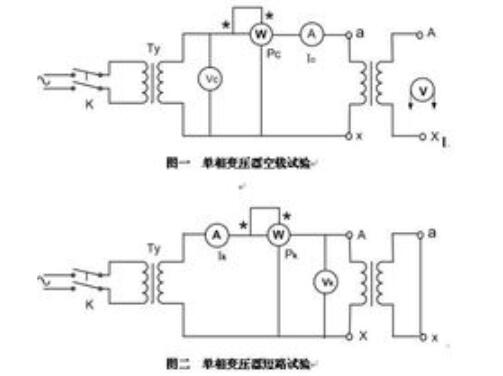
1、  R、L、C 网络.将R、L、C 三元件接成三角形投入三相电网,当L、C 的电抗分别是R 的 1.732 倍时,只要相序合适,R 就是单相负载,且三相对称,功率因数为 1.0 .工频感应炉就这么运行,容量达10 MVA 以上,见图1; 

 图一

 2、 “V”型接法的三相变压器在初级两相间接一电容C,次级绕组串联接一功率因数为0.866的感性单相负载,当负载阻抗是容抗的1.732倍时,初级电流对称,功率因数为0.866(容性),见图2;

     图2

3、在图2的基础上,A、B相间再增加一个电感L,次级负载为纯电阻.L、C 的电抗与折算到初级的电阻相等,则初级电流对称,其大小与折算到初级的电流相等,功率因数为1.0.

上述几方案在应用上的共同特点是:

a、对电网的相序、次级负载性质要求严格;

b、负载要固定.若负载变动,需相应切换储能元件参数.否则将引起初级电流不同程度的不对称.这一缺点方案2 尤为突出.

这就是上述几方案很难在中小功率场合普遍采用的重要原因.

在此说明,只要“三变单系统”里没有非线性元件(合理设计的磁系统在此视为线性),均可逆向运行.例如前苏联早期教科书里能找到上述方案1 的“单相变三相”电路图.

这一特征也适用作为“三变二”问题的平衡变压器.例如,本网站网友jiaoao介绍的“正弦、余弦变三相”的Scott变压器,此时“三变二”已变成“二变三”了.

三、“三变单变压器”——路在何方?

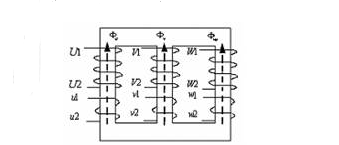
套在三相铁心上的各个线圈之间的不同组合,可产生出不同的合成电势相量.这种相量的辐角可以是30度的任意整数倍,相量的大小可以通过改变线圈的圈数任意获得.

这种三相线圈电势的“相量可组合性”特征给“三变单变压器”的探索者们提供了丰富的想象空间——

拼凑一个单相端口,几乎有无穷多个方案……

总能找出很多个合适的方案……

初级三相线电流不就是几个相量段拼出来的吗?

调整一下相量段,一直拼到三相电流对称难道不可能吗?

问题就出在这儿!

假设某台“三变单变压器”的次级用几个线圈段组合成一个端口(即单相输出端口),这端口电压与产生它的各个相量符合可希苛夫第二定律,或符合某个电压平衡方程式.

或者干脆说:这端口电压是几个电势相量合成的.

但是,这个端口的电流取决于它的负载,与上述相量没有任何关系.再假设这负载电流是 I(I是相量,下同).则任何一个初级线圈电流与次级负载电流 I 的关系由磁势平衡方程式表达.

应注意,不管是哪个初级线圈,磁势平衡方程式所涉的电流相量都与次级负载电流相同,与该线圈所处位置无关.

现把若干个磁势平衡方程式加以整理,得到初级三相线电流的表达式是:
     IA＝K1*I ;
     IB＝K2*I ;
     IC＝K3*I .   (1)
按三相线电流对称的条件,(不对称也没关系,按三线制广义节点的可希苛夫第一定律)必然满足:
     IA+IB+IC＝0
或   K1+K2+K3＝0 (2)

上式说明: a. 由方程组(1)表达的三相电流相量都在一条直线上,不符合“彼此相差120度”的要求;b. 由式(2)可见,三个实常数相加等于0,它们绝对值不可能彼此相等.