基于谱分析的涡街流量信号处理
在仿真分析非整周期采样对谱分析法影响的基础上,对基于谱分析的实际涡街流量信号处理方法进行了有益地探讨。
关键词:非整周期采样;频谱分析;涡街流量信号处理
LIN Min
(Medical Instrumentation College, Shanghai Science & Technology University,
Shanghai 200093, China)
Shanghai 200093, China)
Key words: sampling in non?complete periods; spectrum analysis; vortex signal processing
1引言
涡街流量信号处理的核心问题是扩展涡街流量计在低频段的量程下限。而尝试运用谱分析方法解决这一问题是目前的研究热点之一。文献[1]~[3]采用仿真方法比较了基于FFT的周期图谱法和基于BURG的最大熵谱法,并得出结论:FFT算法所需采样数据多,适合抑制低频确定性噪声;而BURG算法所需数据少,适合抑制随机噪声。但是他们是用信号发生器产生的理想波形来进行谱分析研究的,没有计算实际涡街信号的频谱。另外,该频谱分析是在对信号进行整周期采样的基础上实现的,而实际系统由于未知信号频率,不可能对涡街输出信号实现整周期采样,因而整周期采样只是理想情况,在实际系统中几乎不可能实现。
鉴于此,本文在将谱分析运用到实际的流量信号处理前,有必要先通过Matlab软件来仿真分析非整周期采样对谱分析处理结果的影响,以减少研制中的盲目性和缩短研究周期。
涡街流量信号处理的核心问题是扩展涡街流量计在低频段的量程下限。而尝试运用谱分析方法解决这一问题是目前的研究热点之一。文献[1]~[3]采用仿真方法比较了基于FFT的周期图谱法和基于BURG的最大熵谱法,并得出结论:FFT算法所需采样数据多,适合抑制低频确定性噪声;而BURG算法所需数据少,适合抑制随机噪声。但是他们是用信号发生器产生的理想波形来进行谱分析研究的,没有计算实际涡街信号的频谱。另外,该频谱分析是在对信号进行整周期采样的基础上实现的,而实际系统由于未知信号频率,不可能对涡街输出信号实现整周期采样,因而整周期采样只是理想情况,在实际系统中几乎不可能实现。
鉴于此,本文在将谱分析运用到实际的流量信号处理前,有必要先通过Matlab软件来仿真分析非整周期采样对谱分析处理结果的影响,以减少研制中的盲目性和缩短研究周期。
假设流量计的输出信号为
 ?
?
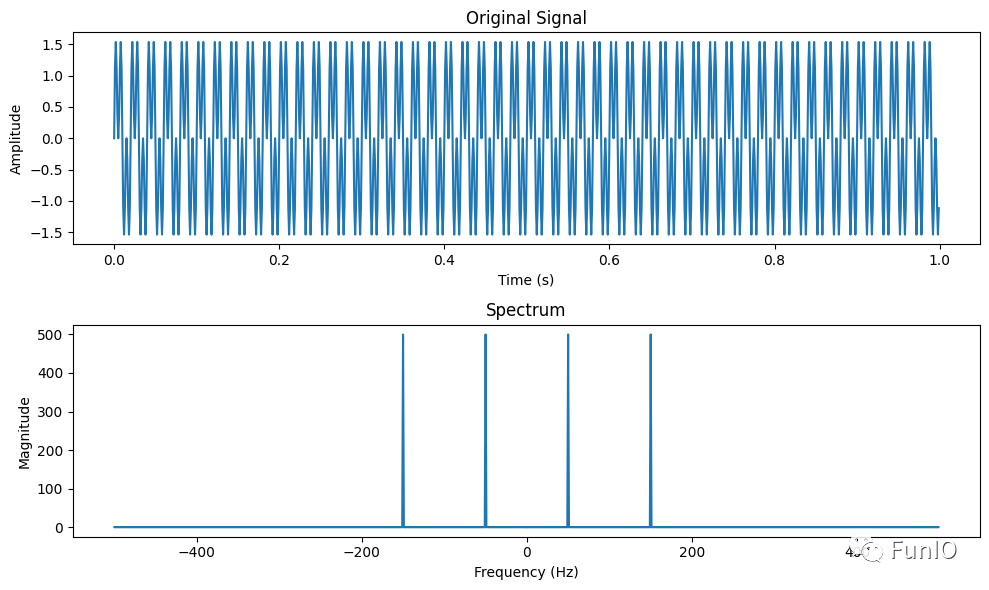
信号频率fsig=20Hz。从t=0时刻开始采样,总采样时间保持不变。则当φ=360°·k,k=0、1、2、…时为整周期采样。为了比较非整周期采样对FFT谱分析和BURG熵谱分析的影响,我们分别取N=1024点、在64个整周期的基础上进行FFT计算以及取N=128点、在16个整周期的基础上进行BURG计算,并令偏移角φ=0°,5°,10°,…,180°,即以5°步长递增来仿真计算非整周期采样对两种算法的功率谱峰值P和频率估计值f的影响。现将两组计算结果分别绘成图1和图2,以供更直观地分析。图中,横坐标代表信号频率值f(Hz);纵坐标代表放大1000倍的功率谱密度值P(W/Hz)。
信号频率fsig=20Hz。从t=0时刻开始采样,总采样时间保持不变。则当φ=360°·k,k=0、1、2、…时为整周期采样。为了比较非整周期采样对FFT谱分析和BURG熵谱分析的影响,我们分别取N=1024点、在64个整周期的基础上进行FFT计算以及取N=128点、在16个整周期的基础上进行BURG计算,并令偏移角φ=0°,5°,10°,…,180°,即以5°步长递增来仿真计算非整周期采样对两种算法的功率谱峰值P和频率估计值f的影响。现将两组计算结果分别绘成图1和图2,以供更直观地分析。图中,横坐标代表信号频率值f(Hz);纵坐标代表放大1000倍的功率谱密度值P(W/Hz)。
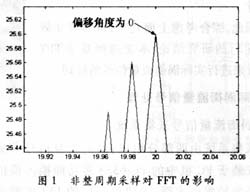
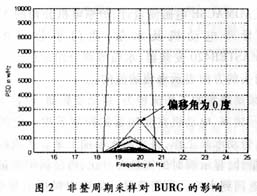
Ⅰ.FFT谱分析在偏角为0°,即整周期采样时谱峰值P最大,对应的频率值f也最精确,为20Hz;随着偏角的增大,谱峰值和频率均减小。而BURG谱分析在偏角为0°时谱峰值P并非最大,但对应的频率值f却最精确,也为20Hz;其谱峰值P与偏角之间无明显的规律关系。
Ⅱ.FFT谱分析随着偏角的增大,其各偏角所对应的频率值近似于线性地递减,即偏角差值相等,所对应的频率差值也近似相等。而BURG谱分析不存在这种规律。
Ⅲ.采样周期数越多,非整周期采样对这两种谱分析的影响越小。例如,FFT谱分析在采样64个周期时的频率误差是采样32个周期时的1/2,是采样16个周期时的1/4,是采样8个周期时的1/8。即检测到的频率误差随采样周期数线性减少而近似线性增大,FFT谱分析在64、32、16、8个整周期采样的基础上偏180°时得到的误差分别为0.77%、1.54%、3.03%、5.88%。
Ⅳ.FFT谱分析得到的功率谱峰值P准确;谱峰值对应的频率值准确。而BURG谱分析得到的功率谱峰值P不准确,前后无规律性;但谱峰值所对应的频率值也准确。
Ⅴ.信号频率值f与采样周期数有关。只要周期数取得足够大时,非整周期采样带来的测量误差就变得很小,可以忽略不计。
因此,综合考虑上面几点,再参考文献[1]~[3]的研究结论,本文选择基于FFT谱分析来进行实际涡街流量信号的处理。?
Ⅱ.FFT谱分析随着偏角的增大,其各偏角所对应的频率值近似于线性地递减,即偏角差值相等,所对应的频率差值也近似相等。而BURG谱分析不存在这种规律。
Ⅲ.采样周期数越多,非整周期采样对这两种谱分析的影响越小。例如,FFT谱分析在采样64个周期时的频率误差是采样32个周期时的1/2,是采样16个周期时的1/4,是采样8个周期时的1/8。即检测到的频率误差随采样周期数线性减少而近似线性增大,FFT谱分析在64、32、16、8个整周期采样的基础上偏180°时得到的误差分别为0.77%、1.54%、3.03%、5.88%。
Ⅳ.FFT谱分析得到的功率谱峰值P准确;谱峰值对应的频率值准确。而BURG谱分析得到的功率谱峰值P不准确,前后无规律性;但谱峰值所对应的频率值也准确。
Ⅴ.信号频率值f与采样周期数有关。只要周期数取得足够大时,非整周期采样带来的测量误差就变得很小,可以忽略不计。
因此,综合考虑上面几点,再参考文献[1]~[3]的研究结论,本文选择基于FFT谱分析来进行实际涡街流量信号的处理。?
3.1涡街流量信号采集系统
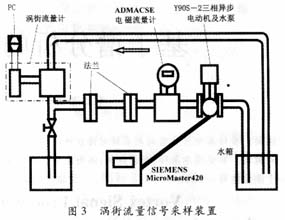
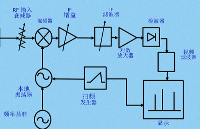
采集系统由两部分组成:涡街流量信号采集装置和可安装于PC机中的PC-6333多功能模入模出接口卡。采集装置由水管、天津仪表厂的LUGB型涡街流量计、ADMACSE电磁流量计、沪东电机公司的Y90S-2三相异步电动机及水泵、西门子公司的MICROMASTER420变频器、水箱等部分组成(图3)。图中,箭头的方向表示水流的流向。
采集装置的工作流程为:启动变频器,设置变频器的显示频率,电动机在变频器的控制下按一定的速度旋转,带动水泵工作,将水从水箱抽上来。水流经过电磁流量计,显示瞬时的流量百分比,再经涡街流量计检测后返回到水箱。涡街流量计的输出模拟信号由PC-6333模入模出接口卡转换成数字信号后送入PC机中再作进一步处理。
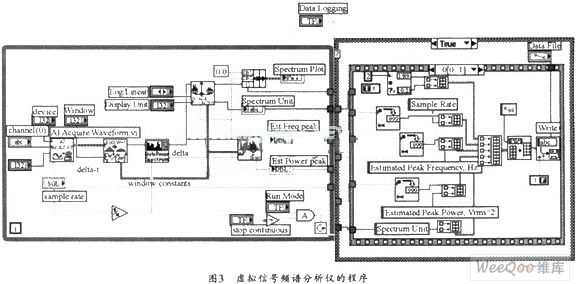
3.2基于谱分析的涡街流量信号处理与分析
通过变频器设置水泵工作频率为50Hz、47.5Hz、45Hz、……,以2.5Hz的步长逐渐降低,当低于35Hz时,水泵电动机就自动逐渐地停止旋转。对应每一个频率点,分别采样2048点数据。将2048点采样数据载入Matlab程序中,通过sptool工具箱对其进行近似整周期FFT计算。为了便于比较和提高计算精度,在每个泵频率点上,我们取了两段不同范围的采样数据,每一段都近似整周期采样,再求取两段的FFT平均值,如图4所示。横坐标表示谱分析得到的频率平均值f(Hz);纵坐标表示各泵频率点上电磁流量计显示的流量平均值(%)。
采集系统由两部分组成:涡街流量信号采集装置和可安装于PC机中的PC-6333多功能模入模出接口卡。采集装置由水管、天津仪表厂的LUGB型涡街流量计、ADMACSE电磁流量计、沪东电机公司的Y90S-2三相异步电动机及水泵、西门子公司的MICROMASTER420变频器、水箱等部分组成(图3)。图中,箭头的方向表示水流的流向。
采集装置的工作流程为:启动变频器,设置变频器的显示频率,电动机在变频器的控制下按一定的速度旋转,带动水泵工作,将水从水箱抽上来。水流经过电磁流量计,显示瞬时的流量百分比,再经涡街流量计检测后返回到水箱。涡街流量计的输出模拟信号由PC-6333模入模出接口卡转换成数字信号后送入PC机中再作进一步处理。
3.2基于谱分析的涡街流量信号处理与分析
通过变频器设置水泵工作频率为50Hz、47.5Hz、45Hz、……,以2.5Hz的步长逐渐降低,当低于35Hz时,水泵电动机就自动逐渐地停止旋转。对应每一个频率点,分别采样2048点数据。将2048点采样数据载入Matlab程序中,通过sptool工具箱对其进行近似整周期FFT计算。为了便于比较和提高计算精度,在每个泵频率点上,我们取了两段不同范围的采样数据,每一段都近似整周期采样,再求取两段的FFT平均值,如图4所示。横坐标表示谱分析得到的频率平均值f(Hz);纵坐标表示各泵频率点上电磁流量计显示的流量平均值(%)。
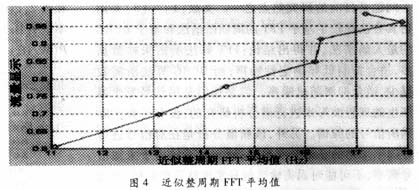
(1)各泵频率点上计算得到的整周期FFT平均值随着“泵频率/流量”值的逐渐降低而减小。
(2)根据用户手册知道LUGB型涡街流量计所能检测到的流体频率范围为13.191Hz~131.91Hz,这是该流量计用传统的电路阈值方法处理涡街信号时的频率检测范围。而用频谱分析方法处理该流量计的涡街信号,在“泵频率/流量”为35Hz/60.58%时得到的涡街信号频率为11.0726Hz,比用传统的电路阈值方法所能检测到的下限频率低2Hz左右。从这点看,频谱分析方法处理涡街信号要比传统的电路阈值方法优越,特别是在测量低流速段时。
(3)本实验选取的采样频率为1kHz,采样点数为2048点,因而频率分辨率
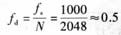
则系统在低流速时的测量相对误差为
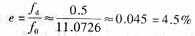
由此可见,若希望测量精度为0.45%,则在信号频率不变的情况下,分辨率应该在0.05Hz以下,在采样点数不变的情况下,则要求采样频率降低到100Hz以下,这就不能满足香农采样定理。若采样频率保持不变,要使分辨率在0.05Hz以下,则采样点数需要增加到20480点以上。可是点数增加则增大数据存储量,同时增大计算量,增加计算时间,会降低系统的实时性。而在采样频率和采样点数一定的情况下,信号频率越低,测量误差越大。对此,用分段设置采样频率的办法以达到同时满足计算精度和系统实时性的要求。进行频率分段,要进行采样频率的频繁切换,这就很难实现在线的信号采集,也很难真正满足系统的实时性,因此该方法不能从根本上解决问题。
(2)根据用户手册知道LUGB型涡街流量计所能检测到的流体频率范围为13.191Hz~131.91Hz,这是该流量计用传统的电路阈值方法处理涡街信号时的频率检测范围。而用频谱分析方法处理该流量计的涡街信号,在“泵频率/流量”为35Hz/60.58%时得到的涡街信号频率为11.0726Hz,比用传统的电路阈值方法所能检测到的下限频率低2Hz左右。从这点看,频谱分析方法处理涡街信号要比传统的电路阈值方法优越,特别是在测量低流速段时。
(3)本实验选取的采样频率为1kHz,采样点数为2048点,因而频率分辨率
则系统在低流速时的测量相对误差为
由此可见,若希望测量精度为0.45%,则在信号频率不变的情况下,分辨率应该在0.05Hz以下,在采样点数不变的情况下,则要求采样频率降低到100Hz以下,这就不能满足香农采样定理。若采样频率保持不变,要使分辨率在0.05Hz以下,则采样点数需要增加到20480点以上。可是点数增加则增大数据存储量,同时增大计算量,增加计算时间,会降低系统的实时性。而在采样频率和采样点数一定的情况下,信号频率越低,测量误差越大。对此,用分段设置采样频率的办法以达到同时满足计算精度和系统实时性的要求。进行频率分段,要进行采样频率的频繁切换,这就很难实现在线的信号采集,也很难真正满足系统的实时性,因此该方法不能从根本上解决问题。
在低流速时,特别是当信号频率在10Hz以下时,涡街信号和噪声信号几乎重叠在一起,甚至噪声的幅值还略大于涡街信号幅值。此时,用功率谱分析方法来处理涡街流量信号,很可能得到的噪声频谱峰值要高于信号频谱幅值,这样就会将噪声频率错认为是涡街信号频率。由此看来,单纯地用频谱分析方法要达到扩展涡街流量计在低流速时的量程下限非常困难。
但是,利用频谱分析能很好地展现信号的频率分布特征,能初步提供涡街信号的频率,为进一步进行涡街信号频率的准确检测做好了准备,提供了研究基础和方向。在频谱分析的基础上,我们设计了涡街信号阈值处理专家系统,并已取得了一定的进展。下一步,我们将继续结合谱分析,运用人工智能和专家系统的方法来处理涡街流量信号,以期能对扩展涡街流量计量程下限的问题有所突破。
但是,利用频谱分析能很好地展现信号的频率分布特征,能初步提供涡街信号的频率,为进一步进行涡街信号频率的准确检测做好了准备,提供了研究基础和方向。在频谱分析的基础上,我们设计了涡街信号阈值处理专家系统,并已取得了一定的进展。下一步,我们将继续结合谱分析,运用人工智能和专家系统的方法来处理涡街流量信号,以期能对扩展涡街流量计量程下限的问题有所突破。
 电子发烧友App
电子发烧友App











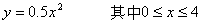













评论