Matlab建立数学模型 - Labwindows/CVI+Matlab建立高频衰减模型

　　首先，以频率f=[0.03，0.1，0.5，1.0，1.5，2.0，2.5，2.7]，以及各频率点对应的功率衰减平均值p=[0.948，1.934，6.995，12.131，13.294，14.269，14.518，14.720]为数据点，画出二维空间的散点图，如图2所示。

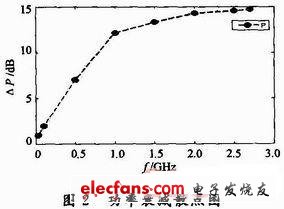
　　根据其分布形状，选取三次多项式作为拟合曲线模型函数：

　　具体实现步骤：

　　(1)将f=[0.03，0.1，0.5，1.0，1.5，2.0，2.5，2.7]，p=[0.948，1.934，6.995，12.131，13.294，14.269，14.518，14.720]写入Matlab命令窗口;

　　(2)输入命令函数cftool，回车弹出“Curve Fitting

　　Tool”窗口，如图3(a)所示;

　　(3)点击按钮“Data”设置拟合数据分别为f，p，如图3(b)所示;

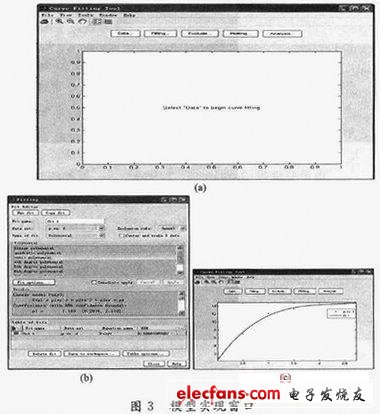
　　(4)点击按钮“Fitting”，弹出窗口“Fitting”，选取拟合函数“cubic polynomial”，点击“Apply”即可得到拟合数据模型，如图3(c)所示。

　　3 LabWindows/CVI实现软件补偿

　　根据依据最小二乘原理拟合得到的高频通道功率衰减模型，采用LabWindows/CVI编程对高频测试仪器进行控制，实现信号功率的补偿，其面板设计如图4所示，软件测试算法流程如图5所示。

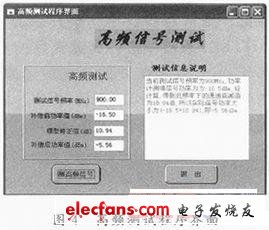
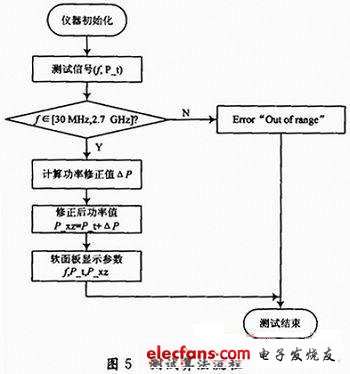
　　以此试验平台为例，外部信号源输出(900 MHz，-5.60 dBm)的高频信号。平台对此信号进行测量，测量结果如图4所示：仪器测得功率为-16.5 dBm，将f=900 MHz带入式(4)，计算的修正值为10.94 dB，所以最终测试结果为(-16.5+10.94)dBm，即-5.56 dBm。这一数据与-5.60 dBm相比较，满足平台测试精度要求。

　　4 结语

　　经试验验证，该方法能有效满足平台测试精度要求，为ATS测试高频信号提供了一种实用的方法。