多元回归分析 - 基于测量数据的电磁兼容性能参数建模的研究

　　其大致步骤如下：

　　(1)将输入自变量作为横坐标，输出量即测试值作为纵坐标，描绘出测试曲线。

　　(2)对所描绘的曲线进行分析，确定公式的基本形式。如果数据点基本成一条直线，则可以用一元线性回归方法确定直线坐标。如果数据点描绘的是曲线，则要根据曲线的特点判断曲线属于何种函数类型。可对比已知的数学函数曲线加以对比、区分。如果测试曲线很难判断属于何种类型，则可以按多项式回归处理。

　　(3)确定拟合方程中的常量。可根据一系列测试数据确定方程中的常量。

　　(4)检验所确定的方程稳定性和显著性，用测试数据中的自变量代入拟合方程计算出函数值，看与实际测试值是否一致。差别的大小通常用标准差来表示，进行方差分析，F检验等。如果所确定的公式基本形式有错误，此时应建立另外形式的公式。

　　在进行研究分析的时候，考虑某功率放大器放大倍数的变化情况。假设经过数据统计得到此功率放大器的放大倍数情况如表1所示。

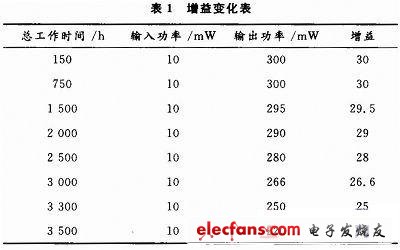
　　2.2 建模与仿真

　　根据表1所给的数据，运用回归分析的方法对放大器的增益参数进行建模，在置信水平为95%的条件下按照回归分析的步骤得到其随工作时间的变化曲线，如图2所示。

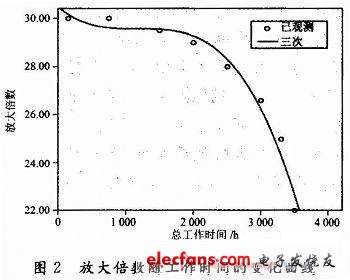
　　由图2可以看出当用三次多项式作为其数据模型时能比较好的拟合所给的数据，对其进行参数估计和模型汇总得到各参数的基本情况如表2所示。

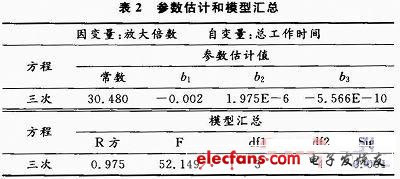
　　根据表2的数据及F检验法的判断标准可知此方程回归效果显著，由此可根据此方程得到因变量增益的预测值和置信区间，具体数据如表3所示。

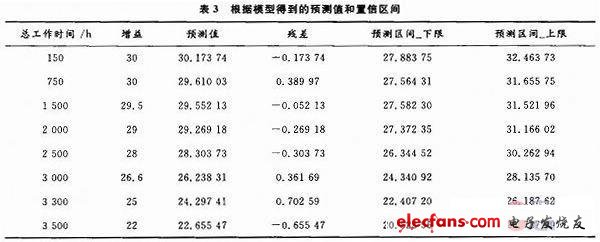
　　3 结语

　　回归模型是分析测试数据很重要的工具，可以得出的是参数之间的变化关系，也许单独某对参数之间的变化关系不足以提供有意义的信息，还可以建立多元回归模型来研究多个参数和某个参数之间的变化关系。由于回归分析在非线性分析中的局限性，在以后的工作中将着重研究人工神经网络在此方面的应用。参数模型建立的方法并不是固定的，随着研究点的不同，模型的选择也不同。通过所建立模型，可以不需要进行实际测量来预测电子系统未来的电磁兼容状况，有效指导系统的电磁兼容性分析和保障。