量纲误用在科学计算程序中是一种常见的错误,然而程序设计语言的标准类型系统却对此无能为力。物理方程中的量纲错误可以手工分析出来,然而求解物理方程的计算机程序中的量纲错误却难以被发现,因为计算程序往往很复杂。例如,一些研究者认为火星气候探测卫星的丢失,是因为程序中把一个英制单位的变量传递给了使用公制单位的模块。因而,量纲的正确性对计算结果的正确性非常重要。
近年来,研究者们提出了一些量纲检测方法,典型的如Osprey量纲检测方法。Osprey方法包含5个主要步骤:
(1)对待检测源程序进行单位标注,使得检测器能够知道每个变量的单位;
(2)C语言解析和语法检查;
(3)生成包含单位信息的抽象语法树;
(4)生成约束CY程);
(5)方程的化简及高斯消去求解(GE)。
可以看出,Osprey方法步骤较多,每步都需要语言外的其他工具,并需要对其进行修改、扩充,而且最后的高斯消去(GE)计算量非常大,是Osprey方法的性能瓶颈。使用Osprey方法还有一个问题,就是需要同时维护2份源代码:一份正常代码用于编译测试;另一份包含量纲信息的检测代码,修改正常代码后必须及时对检测代码进行更新,维护起来也比较繁琐。此外,由于C++语言的解析非常困难,Osprey方法目前没有实现对C++程序的量纲检测。
针对这些问题,提出一种基于模板元编程的量纲检测方法TADA(TMP-bAsed Dimensional AnalysisMethod),其基本思路是利用程序设计语言自身的模板元编程(Template Meta Programming,TMP)功能,让编译器在编译时对程序中的量纲进行准确性检测,从而可以避免Osprey方法的计算量大等诸多问题。TADA方法具有下列优点:
(1)TADA方法可使得应用开发人员不需要维护2份代码,因为使用TADA方法的检测程序也完全是一个合法的可编译的程序。
(2)TADA方法的量纲检测完全在编译期间进行,对程序不会引入任何运行时开销。
(3)TADA方法无需进行方程组求解工作,可以适用于任何规模的程序。与Osprey等方法类似,TADA方法也需要手工对程序添加量纲信息,其标注的工作量与Osprey等方法相当。但TADA方法中编译器在进行检测的时候无需进行Osprey方法中的方程组求解工作,因而不再有Osprey方法的计算瓶颈。
(4)TADA方法采用模块化设计,使得单位的表示与匹配检测之间实现了松耦合,支持用户可以以一致的方式增加新的单位。
1 模板元编程(TMP)技术
在C++程序设计语言中,模板元编程是实现代码重用的一种重要机制。下面首先对模板元编程技术进行介绍,然后给出TADA方法中需要使用的几个基本的模板元程序。
1.1 模板元编程简介
模板可以将类型定义为参数,以提高代码的可重用性。模板包括类模板和函数模板等。函数模板与模板函数的区别可以类比于类与对象的区别:函数模板是模板的定义;而模板函数是函数模板的实例,具有程序代码,占用内存空间。当编译系统发现了函数模板一个对应的函数调用后,根据实参的类型来确认是否匹配函数模板中对应的形参,然后生成一个重载函数,称该重载函数为模板函数。类似地,在声明了一个类模板后,也可以创建类模板的实例一模板类。
类模板的一般形式如下:
template
class类名{
//类定义…
};
C++模板系统能够通过模板的特化、偏特化实现逻辑判断,并能通过模板递归实现循环,构成了一个图灵完全的二级语言。使用这种二级语言进行编程叫作C++模板元编程(Template Meta Programming,TMP)。模板元编程的驱动力是模板的递归实例化。
下面给出C++模板元编程的一个示例。
首先定义一个类模板,通过该类模板可实现在编译期间计算4的任意次方。如下所示:

通过下面的程序来使用该模板。

程序Test.cpp执行完后,会正确输出4的7次方的值,该数值是C++编译器在编译模板元程序时递归计算得到。由于模板元程序完全在编译期间执行,相当于对编译器功能进行扩充,因而利用这种程序进行量纲检测具有良好的可行性。
1.2 基本模板元程序
下面给出TADA方法中需要使用的几个基本的模板元程序。
(1)静态判断

语法:StaticlF
语义:当cond为真时,ResuhType为T1,否则ResuhType为T2。
(2)静态断言
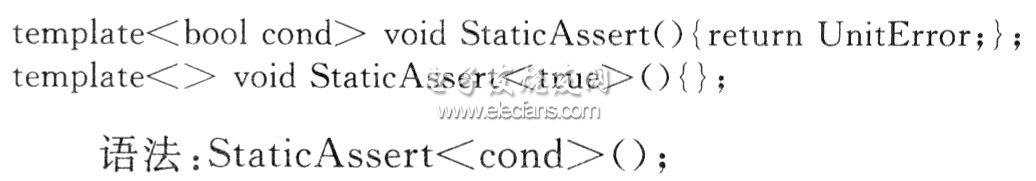
语义:当cond为真时什么也不做,否则产生一个编译期错误(UnitError没有定义,或void函数不应该有返回值)。
(3)静态绝对值


语义:递归的使用辗转相除法在编译期间求出a与b的最大公约数,其中a与b为int类型。
2 TADA量纲检测方法
TADA量纲检测方法需要涉及到单位和量纲的表示、计算、标注以及数学运算函数的量纲包装等各个组成步骤,下面将依次对其进行介绍。
2.1 单位和量纲的表示
在Osprey方法中,量纲是用一个长度为7的向量表示的,每个分量对应一个SI标准量纲。TADA方法中也采用了这种方式。为了简化阐述,本文只讨论长度、重量、时间这三种量纲,其SI单位分别为米、千克和秒(TADA方法可直接推广到其他各种量纲)。由于TMP程序的特殊性,它并没有数组或向量的支持,也不能使用浮点数据(使用浮点数表示量纲也会带来不精确性),量纲在TMP程序中的表示形式有所不同:用u11,u12,u21,u22,u31,u32之类的整型量分别表示
,
并辅以ratio表示同量纲、不同单位之间的比值,如分钟和秒的比值为60。
TADA方法可静态地建立如下常用单位:

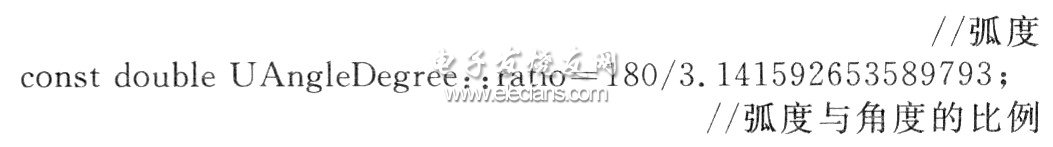
模板元程序在计算公式的时候需要推导出新的量纲,例如在计算
的时候,编译器应该能根据等号右边的公式计算出它的量纲,并与e的量纲进行比较判别。TADA方法的量纲是用分数形式表示的,在每次量纲计算之后都需要进行分数的约分处理,才能进行相等性判断,因而TADA方法可用如下的方式处理新生成单位,如下所示。

2.2 单位和量纲的计算
由于量纲都是用分数表示的,因而其计算会稍有麻烦。下面定义TADA方法中量纲分数的加、减、乘、除和等价测试运算。
(1)分数的加法运算,如下所示。

(2)分数的减法运算。TADA方法通过加法实现减法计算,如下所示。

语义:分数相减并约分,即:
(3)单位相乘。分别将3个量纲分数相加,然后使用BuildUnit生成新单位。

语义:单位Ua与单位Ub相乘后的新单位。
(4)单位相除。与乘法处理方式相似。

语义:若单位ua与单位Ub等价则不产生任何效果,否则产生编译期错误。
2.3 单位和量纲标注的原理和语法
与Osprey等方法类似,TADA方法也在待检测源程序进行单位标注,以使得检测器能够知道每个变量的单位。由于经过单位标注的待检测程序仍然是合法的可编译的程序,所以标注信息必须由语言自身已有的语法要素构成;标注信息还不能影响被标注变量的任何计算特性及使用方式,只有满足这两点要求的标注方式才能使标注工作量最小化。此外,已标注变量应该禁止从未标注变量进行各种隐含的类型转换,这样严格的限制才能有效进行单位量纲的匹配检测。对于C++语言来说,可以采用模板类的方式实现。
标注实质上是把语言原始的数据类型替换成TADA方法预定义的模板类,而模板类实现了各种运算符号的重载,同时禁止了任何隐含的类型转换,使得量纲标注既满足语法要素的要求,又满足计算兼容性的要求和禁止隐含转换的要求。TADA方法中标注的实现如下所示。


2.4 定义单位量纲
量纲检测系统应该预定义常用单位量纲,以方便应用开发人员使用。TADA方法采用如下方式定义单位量纲:


2.5 数学运算函数的量纲包装
对于指数、对数、三角函数等已有的数学运算函数,其参数与返回值都是没有单位量纲的,不能直接用于有量纲的公式计算。针对这个问题,.TADA方法提供了这些函数的量纲包装,以sqrt和sin为例如下:

2.6 辅助工具
TADA方法还提供了一些辅助工具,用于将量纲变量以适合阅读的方式显示出来,例如:
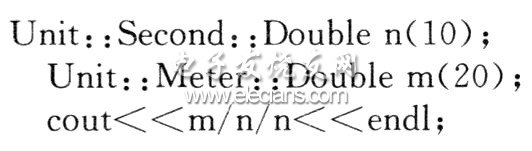
可以得到这样的输出结果:0.2米/秒2
2.7 分析和评估
在TADA方法的基础上,实现了面向C/C++程序的量纲检测系统(TADA系统),并对TADA系统的检测能力进行了分析和评估。
首先采用TADA系统来检测下面的样例程序。

在TADA系统中,Visual Studio 2003编译该程序会出现类似如下的错误信息,错误信息的第3行就表明了unit.epp的第9行有错误。

在检测能力方面,采用文献的样例程序对TA-DA系统和Osprey系统的量纲检测能力进行了对比评估。在文献中,Osprey共找到了3个错误,其中前2个是单位误用错误,第3个是单位转换比例因子错误。TADA系统也完全找到了前2个错误,而第3个错误在标注时被避免掉了,因为该单位系统包含了量纲之间的比例因子,能够进行自动的单位转换。
在性能和可扩展性方面,TADA系统能够更有效地实现对c/c++程序的量纲检测。Osprey系统引入了具有较高计算复杂度的线性方程组求解步骤,需要很大的计算和时间开销来解线性解方程组。TADA系统基于模板元编程技术,只需要利用语言自身的语法能力,靠编译器进行单位量纲检查,没有带来太多额外的复杂计算。并且TADA系统不会带来任何程序的运行时开销。因此TADA系统可适用于各种规模的C/C++程序,具有更好的性能和可扩展性。
在易用性方面,TADA系统的标注负担与Osprey系统相当。由于TADA系统利用C++编译器的功能进行错误检测,而C++编译器遇到模板错误时的错误信息却不很直观,错误报告的可读性较弱,但仍可以快速定位到错误点。
3 结 语
这里提出一种新颖的基于模板元编程的单位量纲检测方法TADA,并基于该方法实现了一个单位量纲检测系统。
TADA方法采用模板元编程技术,使得经过单位量纲标注的受测程序仍然是一个完整、合法、可编译的C/C++程序,无需维护多套程序代码,也无需进行复杂的解方程组运算,就能够在程序代码中发现量纲错误,具有良好的实用性和可扩展性,可以有效适用于多种规模程序的量纲检测。
 电子发烧友App
电子发烧友App




















评论