数字设计基础知识--频率与时间
在低频时,一段普通导线可以有效地将两个电路短接在一起,但在调频时就不同了。高频状态下,只有宽的,扁平的,导体才能够有效地短接两个电路。同样一段导线,在低频时有效的,但在调频状态下因电感太大而无法完成短接功能。我们可以把它用做一个调频电感,而不是一个调频短接电路。
这是一个普遍现象吗?难道在某个频率范围工作正常的电路元件在另一个频率范围就无法工作吗?电气参数对频率真的如此敏感吗?
的确如此,如果以对数频率为一个坐标轴,几乎没有哪个电气参数在超过10个或20个十倍频程的范围内依然能够保持为常数。因此,对于每个电气参数,我们必须考虑其有效的频率范围。
为了进一步阐明这个极宽的频段范围概念,首先来考虑对应极长时间周期的一个极低频率,随后将讨论在极高频率时的情况。
一个10的-12次方HZ的正弦波每30000年才完成一个周期。TTL(晶体管-晶体管逻辑)电平的10的-12次方HZ正弦波平均每天中相应的变化值比1UV还小。这的确是一个非常低的频率,但并不等于零。
有关半导体10的-12HZ频率的任何实验,最后都不可能实现。完成10的-12次方HZ频率的实验所需的时间实在是太长,以致于电路已经化为灰烬了,在这样长的时间段内观察,集成电路只是一小块氧化硅而已。
当我们把频率急剧提高时,时间周期会变得非常短,那此电气参数也会发生变化。例如在1KHZ时,一段短的接在导线经测量得到的电阻为0.01欧,而在1GHZ时,由于趋肤效应,电阻增加到1.0欧,不仅如此,还得到了50欧的感抗。
当频率上升至电路元件工作频率范围的上限时,元件性能常常会发生较大的变化。
多高的频率范围对于高速数字设计才重要呢?图1.1回答了这个问题,图中描述了一个随机数字脉冲序列与其频谱的重要部分之间的关系。

图1.1所示的数字信号是由一个D型触发器输出的,其时钟频率为F。在每个时钟周期,数据的值在1和0之间随机地触发。在这个例子中,10~90%上升和下降时间记为T,为时钟周期的1%。
如图1.1所示,这一信号的频谱功率密谋在时钟频率的各个倍频上显示为空,而且从F向上直到标记为F的频率点,总的斜率为-20DB/DECADE。超过F,频谱滚降则大大快于20DB/十倍频程。而在转折频率点F,频谱功率的幅值比按20DB/十倍频程滚降的预期值低了一半。对于任何数字信号,转折频率与其数字边沿的上升(和下降)时间有关,而与它的时钟速率无关:

其中,F=转折频率,数字脉冲的大部分能量集中在该频率以下T=脉冲上升时间。
缩短上升时间会提高F频率。拉长上升时间则会降低F频率。
任何数字信号的重要时域特性主要由F频率以下的信号频谱所决定,从这一法则我们可以定性地推导出数字电路的两个重要特性:
1、任何在其F频率以内具有一个平坦频率响应的电路,可以允许一个数字信号几乎无失真地通过。
2、数字电路在F频率以上的频率特性对于它如何处理数字信号几乎没有影响。
注意:F只由信号上升时间定义,而且与其他频域参数没有直接参与联系。这个简明的定义使得F容易使用,而且容易记忆。
当使用F的时候,应该记信这是一种不精确的频谱测量方法。作为一个参考标志,F能帮助我们把频率影响的结果区分为完全无关紧要的、或者仅仅是令人不安的以及完全破坏性的等几个级别。在大多数数字问题中,这正是我们所希望的知道的。
当然,F也有局限性,F不能精确地预测系统的工作情况,甚至也不能精确地定义如何测量上升时间!F不能代替已经成熟的傅里叶分析方法,也不能用来预测电磁辐射。电磁辐射的特性取决于F频率以上部分的具体频谱的情况。
同时,对于数字信号,F能够以实用而有效的方式迅速地将时间和频率联系起来。我们将在本书中通篇使用F作为数字信号所含频谱成分的实际上边界。
加到前述推导的特性1,如果系统在F之下的频率范围内有一个非平坦的频率响应,那么它是如何使数字信号产生畸变的呢?这里有一个例子。
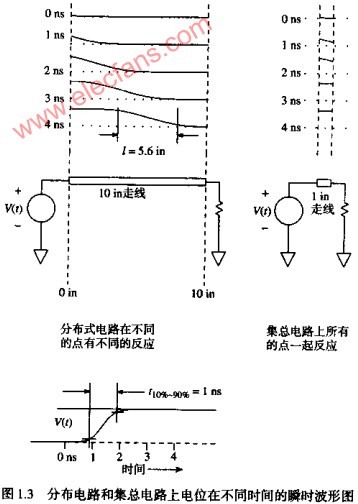
我们知道,一个电路的调频响应影响它对瞬时过程的处理(比如上升时间)。电路的低频响应影响它对长期过程的处理。图1.2说明了一个电路在调频和低频时具有不同特性。这个电路可以通过调频变化,但是不能通过低频变化(长期的稳定部分)。
让我们从一个特定频率F开始分析图1.2。在频率F,电容C具有一电抗(也就是阻抗的大小)为(C2πF)
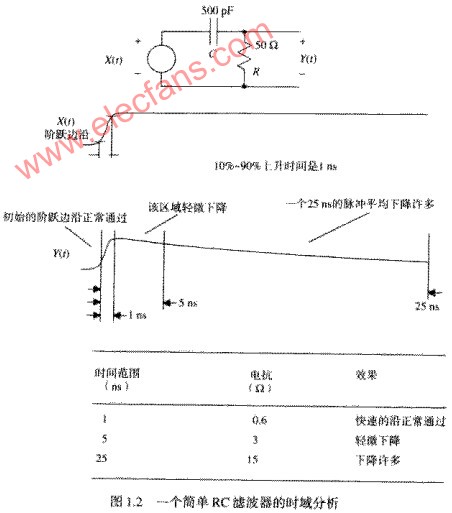
我们用这个公式计算电抗议并且用上升时间替换F:

其中,TR=阶跃输入的上升时间,S
F=阶跃输入的最高频率,HZ
C=电容,F
式中显示了如何用转折频率或上升时间来估算一个电容的电抗。
在图1.2的电路中,一个0.6欧的电抗实际起一个短接的作用。全振幅的脉冲前沿将直接冲过这个电容。
时间间隔超过25NS,容性电抗增加到15欧,导致耦合信号的幅度显著下降。
本文地址:http://www.elecfans.com/article/88/131/189/2010/20100528218628.html
 电子发烧友App
电子发烧友App










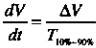












评论