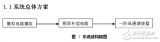
极点的定义是输出变为无穷大,极点的存在会给电路的不同频率的小信号带来不同的反应,唯一的极点就在输出Vout,输出阻抗Rout等于上面那个resistor和下面的ro并联,当小信号的频率变得非常大之后,系统对极高频率的信号也就无限衰减了。
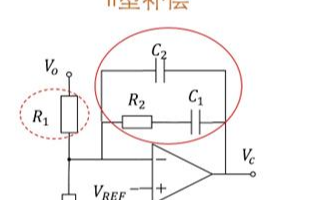
我们来看看一个单极点的电路,看看极点的存在到底是如何影响了电路对不同频率的小信号的反应。
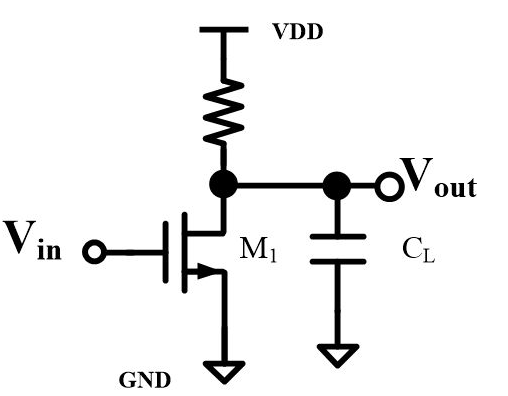
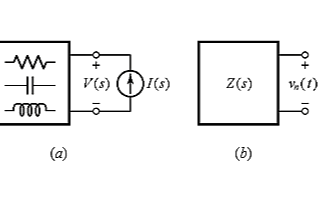
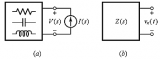
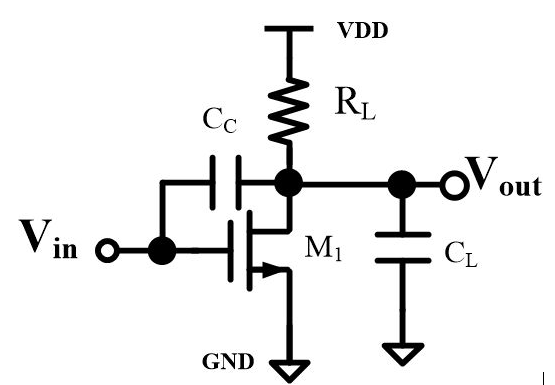
一个nmos和一个resistor,组成了一个基本的common-source amplifier。暂时忽略Cgs、Cgd等寄生电容造成的高频零极点。这个电路便是一个单极点系统:唯一的极点就在输出Vout那里。当然,还有一个前提就是我们的load capacitor比较大,比如就用1pF好了。输出阻抗Rout等于上面那个resistor和下面的ro并联,嗯,总之就是很简化的一个模型啦!
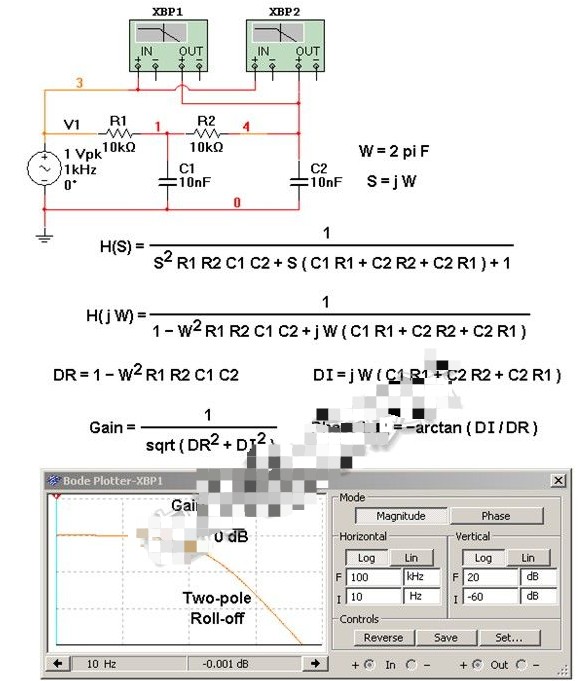
然后,我们可以根据
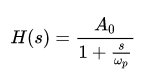
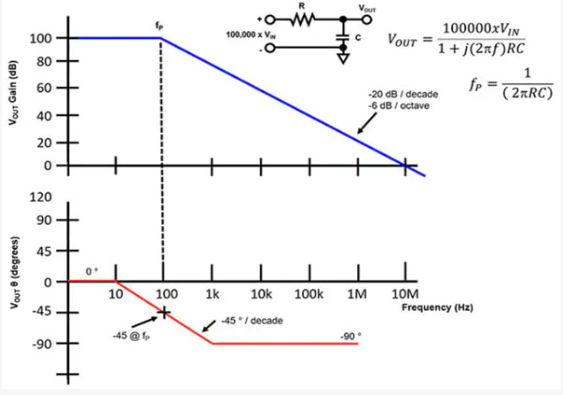
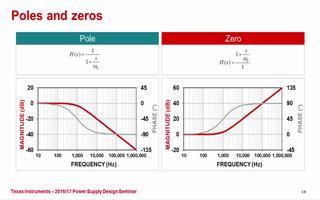
得到这个单极点电路的transfer function的波特图:
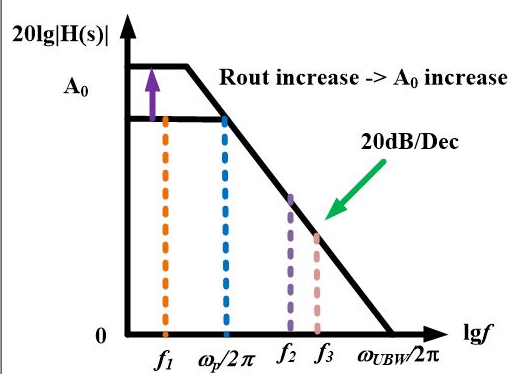

再之后,当小信号的频率变得非常大之后,分母项远大于分子,这个系统对极高频率的信号也就无限衰减了。
等等!为什么大家都说-20dB/dec呢?就是说,为什么超过了极点之后,频率每变大十倍,增益就下降20dB呢?
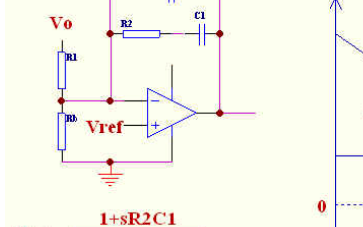
这个嘛……我们还是回到之前的公式仔细看看:
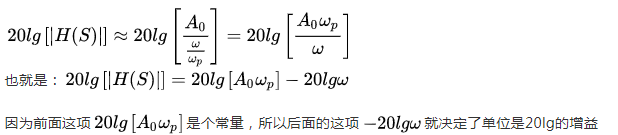
下降的速度。比如在上面的图中,假设f3的频率是f2的十倍,那么f3对应的增益大小自然也就比f2少了20dB。
好吧,下降的速度我们算是搞明白了。那到底什么时候,这个单极点的amplifier就完全失灵,完全不能放大输入的小信号了呢?
这样,一个新的频率 unity-gain bandwidth就冒出来了呢。
在这个频率UBWB处,这个amplifier的gain下降到了1,也就是20lg1,就是0dB了。
好吧,那这个频率到底是多大呢?
其实,我们就用最基本的线性方程来求解就可以了的。
首先,我们知道,在Wp时,纵坐标大约是20lgAo;然后,我们还知道了斜率是-20dB/dec,嗯,这样不就可以了嘛?
等等!到底怎么算的?

仔细一看,这个UBW的公式里面只有gm和C,跟具体的Rout大小完全没有关系呢!所以,上面那个波特图的DC gain Ao可以因为Rout变大,而变大,但是这个电路的UBW却还是一点都没有变呢!
嗯,写到这里,一个基本的单极点amplifier的频率响应,也就差不多了。
最后, 还想强调一下,一定要是小信号才能这样分析啊!
试想一下,如果你的input 电压忽然从0变成了VDD,输出也就差不多从VDD变成了很接近0的一个值。那你试试算它的增益?是不是顶多是1?为啥呢?即使从0到VDD变换的速度可以很慢,也可以很快,增益绝对不会超过1……
因为这是大信号了啊!
不是说好了的吗?上面所有的这些分析,都是基于小信号的啦!大信号就不适用了啦!
那个……到底在哪里区分大信号和小信号呢?
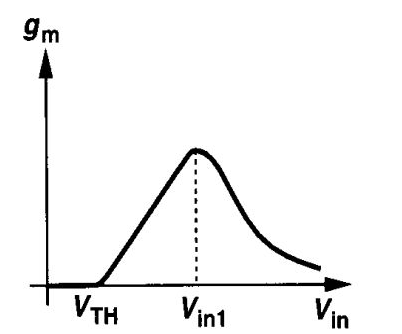
不过 还是可以告诉大家,这样的图是咋plot出来的(Razavi, p51):
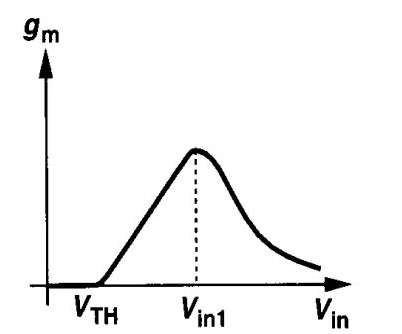
在Cadence里面,input端放一个vdc (在library : analogLib里面),把它的DC value设置成一个变量,比如vdc_in好了。然后用DC sweep,设置这个vdc_in的范围,比如从0到VDD(其实这样大的范围没啥意思哈!稍微小一些,细节会比较清楚。)然后plot输出端看到的current除以这个vdc_in,就拿到了上面这个gm的图。其实也差不多是这个单极点电路的增益随着input电压的变换趋势啦。
当然,为了看仔细点,我们还是先定下DC biasing 好了。比如input有个DC的电压,一直固定在0.5V,这个时候看到的output的DC值是0.6V。然后还是跟上面一样,DC sweep一个加在0.5V的input biasing上面的变量,比如从-10mV到10mV。得到的输出电压减去之前的0.6V,然后除以input的变化范围20mV,也就得到了这个电路的DC增益了!
对于一个典型的比较成熟的工艺,比如180nm这样的,一个单级的nmos,它的最大gain差不多能够达到40dB的样子。当然,能不能拿到这个值,跟你的具体DC biasing voltage和上面的resistor大小都是很有关系的。嘿嘿,你们还是自己去试试吧!
总之,只有当一个transistor被bias在合适的DC operation point,它的最大增益效能才能被充分的发挥啊!
 电子发烧友App
电子发烧友App









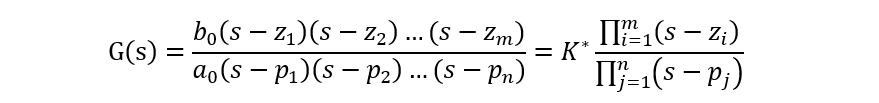

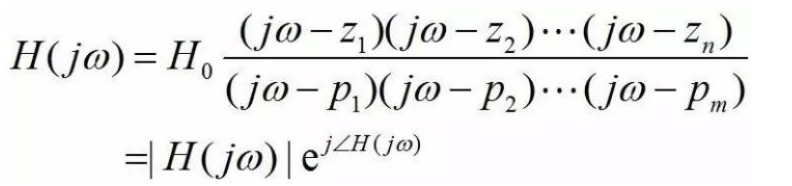

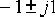










评论