同加法运算一样,减法运算可采用减法器来实现。半减器和全减器的设计方法和步骤与设计加法器相同。实用上,为了简化系统结构
,通常不另外设计减法器,而是将减法运算变为加法运算来处理,使运算器既能实现加法运算,又可实现减法运算。一般采用加补码的方法代替减法运算,下面先来介绍这种方法的原理。
1.反码和补码
这里只讨论数值码,即数码中不包括符号位。以前应用的自然二进制码称为原码,所谓反码就是将原码中的所有0变为1,所有1变为0后的代码。观察如下几组原码与反码之间的关系。

显然,每组反码都是从1111中减去原码的结果,所以,可得如下反码与原码的一般关系式:N反=(2n-1)-N原
其中N等于数码的位数。
定义补码为:N补=2n-N原
于是,便可得到补码和反码的关系式:N补=N反+1
由以上分析可知,一个数的反码可将原码经反相器获得,而由反码加1就可得到补码。
2.由加补码完成减法运算
由反码与原码的一般关系式可得两数A、B相减的表达式:

上式表明A减B可由A加B的补码并减2n完成。
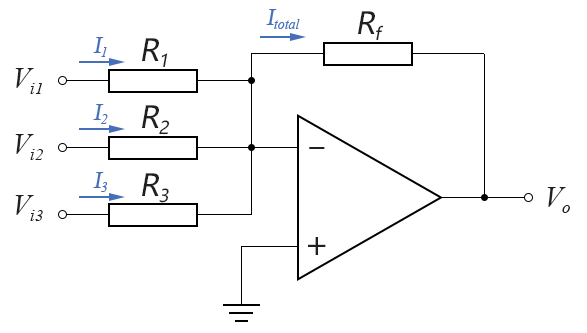
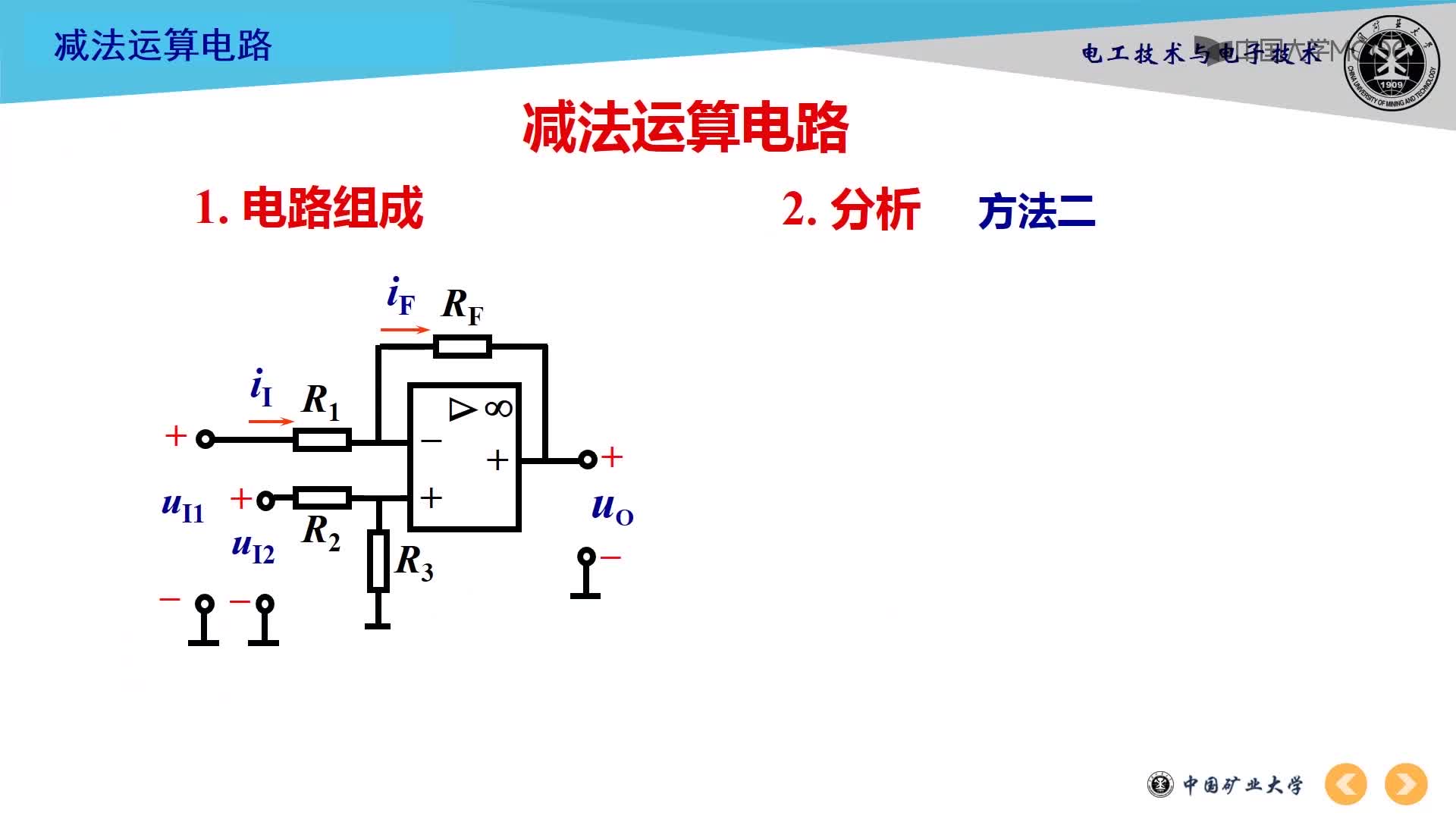
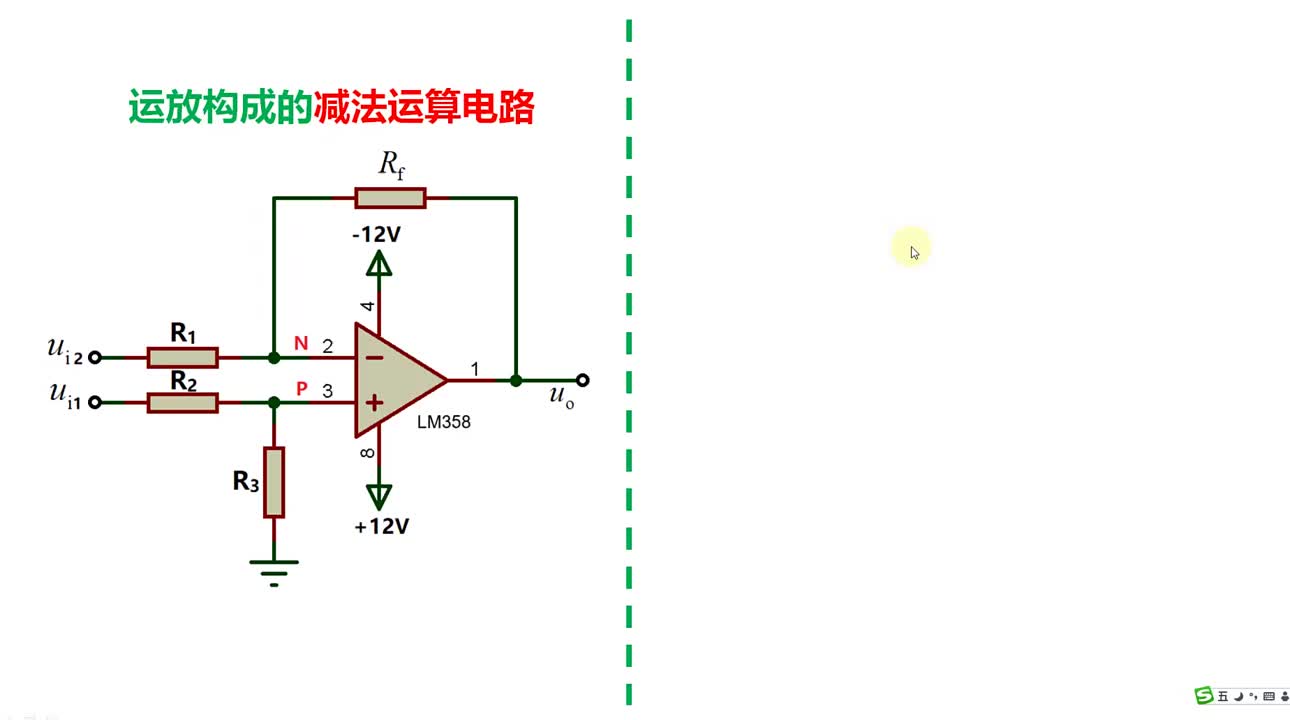
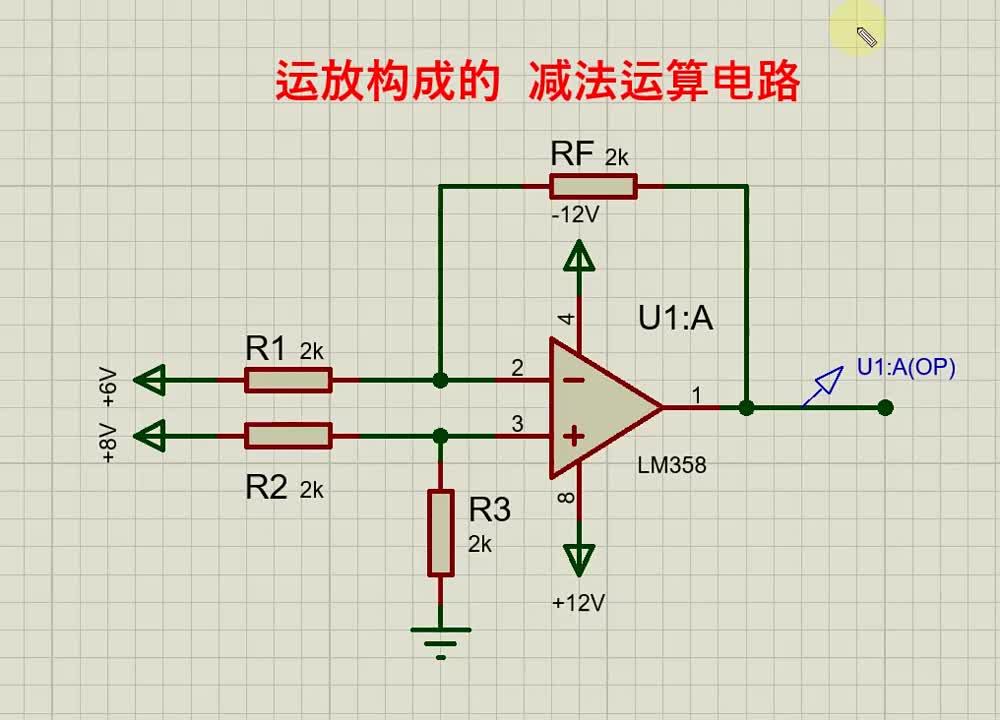
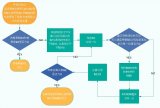
下图为4位减法运算电路图:

由4个反相器将B的各位反相(求反),并将进位输入端C-1接逻辑1以实现加1,由此求得B的补码。显然,只能由高位的进位信号与2n相减。当最高位的进位信号为1(2n)时,它们的差为0;最高位的进位信号为0时,它与2n相减所得的差为1,同时还应发出借位信号。因此,只要将最高位的进位信号反相即实现了减2n的运算,反相器的输出V为1时需要借位,故V为借位信号。下面分两种情况分析减法运算过程。
(1)A-B≥0的情况。
设A=0101,B=0001。
求补相加演算过程如下:

直接作减法演算,则有 
比较两种运算结果,它们完全相同。在A-B≥0时,所得的差就是差的原码,借位信号为0。
(2)A-B<0的情况。
设A=0001,B=0101。
求补相加演算过程如下:

直接作减法运算,则有:
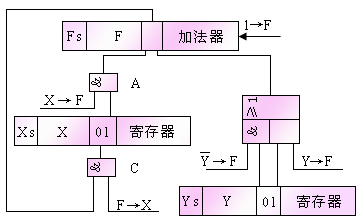
比较两种运算结果可知,前者正好是后者的绝对值的补码,借位信号V为1时表示差为负数,V为0时差为正数。若要求差值以原码形式输出,则还需进行变换。由补码的定义式可知 ,即将补码再求补得原码。这时的求补逻辑电路如下图所示:
,即将补码再求补得原码。这时的求补逻辑电路如下图所示:

结合4位减法运算逻辑电路和这个求补逻辑电路可组成输出为原码的完整的4位减法运算电路。求补相加而得的差输入到不同的异或门的一个输入端,而另一输入端由借位信号V控制。当V=1时,D3~D0反相,加法器也不实现加1运算,维持原码。
 电子发烧友App
电子发烧友App


































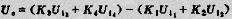











评论