本文基于估计理论和模糊系统理论,提出了一种多传感器多回波模糊一概率交互作用的数据关联滤波算法,以解决密集杂波干扰环境中多传感器跟踪机动目标的数据关联问题.模糊关联度和关联概率共同组成了各有效回波的加权系数,弥补了概率数据关联滤波方法(PDAF)的不足.提高了杂波环境中机动目标的跟踪性能.
关键词:模糊逻辑——概率交互作用;数据关联;密集杂波环境;机动目标跟踪;多传感器数据融合
Multisensor Fuzzy-Probability Interacting Data Association Algorithm
LIU Yuan XU Lu-ping
(School of Electronic Engineering,Xidian University.,Xi'an 710071,China)
XIE Wei-xin
(Shenzhen University,Shenzhen 518060,China)
Abstract:Based on the theory of the estimation and fuzzy logical system,this paper proposes a data association algorithm of the fuzzy logic-probability interacting,to solve the data association problems typically encountered in the application of multisensor in tracking a maneuvering target in a heavily-cluttered environment.The combination of fuzzy association degree and probabilistic association forms the weights that the ith received measurment is target originated.The proposed data association algorithm counteracts the weaknesses of probabilistic data association filter (PDAF),and improves the performances of tracking a maneuvering target in a heavily-cluttered enviroment.
Key words:fuzzy logic-probability interacting;data association;heavily-cluttered environment;multisensor tracking maneuvering target;data fusion
一、引 言
在密集杂波干扰环境中,跟踪机动目标的困难在于众多回波与目标航迹关联的不确定性.它使我们无法确定哪一个回波来自于真实的目标.目前,杂波干扰环境中,跟踪单目标的数据关联算法中最有代表性的是概率数据关联算法(PDAF),它通过计算位于跟踪门内所有回波的加权平均来更新目标航迹.但在密集杂波干扰环境中,当跟踪门内平均杂波数达2后,该算法将有可能产生错误的数据关联[1],而导致目标丢失.经研究发现,在目标匀速或匀加速运动期间,PDAF可以较好地实现目标的跟踪.一旦目标出现机动,就容易产生数据关联错误.这是因为PDAF的实质是计算多回波的统计中心.它是所有有效回波的加权平均,各权重的大小与该回波和目标预测值之间的距离,即新息的大小紧密相关.当目标出现强机动,既使采用多模型自适应跟踪方法,由于密集杂波干扰,真实目标回波新息也将增大,从而它的关联概率将减小,这必将导致真实目标回波新息的进一步增大.这种不良循环,最终导致关联失败和目标丢失.可见,单用PDAF关联方法,不能有效解决密集杂波干扰环境下的机动目标跟踪问题.
本文给出了一种多传感器模糊逻辑-概率交互作用的数据关联滤波方法.使用模糊逻辑解决数据关联问题的理由:一是数据关联问题本身的不确定性或模糊性,正是模糊逻辑研究的对象.二是应用模糊逻辑可以快速建立目标特征空间与关联度空间之间的非线性映射关系模型.该模型可以融合数字,语言等多种信息,具有良好的鲁棒性.一些有效的自学习方法可用于支持建模.模糊关联方法可以有效解决目标机动期间的关联问题,弥补了PDAF的不足,提高了系统的数据关联性能.多传感器目标状态估计采用序列估计法[2]实现,估计精度明显高于单传感器目标状态估计.
二、多传感器目标跟踪的模糊滤波算法
目标的动力学方程为:
X(k+1)=Φ(k)X(k)+W(k) (1)
这里X(k)是k时刻n维状态矢量,Φ(k)是n×n维状态转移矩阵,W(k)是n维状态噪声,假设其均值为零,方差为E{W(k)WT(l)}=Q(k)δkl的正态分布.
如果量测来自被跟踪的目标,则第i个传感器量测方程为
Zim(k)=Hi(k)X(k)+vi(k) (2)
其中Zim(k)是测量矢量,Hi(k)是已知的m×n维测量增量矩阵,vi(k)是m×1维的测量噪声,设它为正态分布,其均值为零,方差为E{vi(k)viT(l)}=Ri(k)δkl.
如果量测不是来自被跟踪的目标,既为杂波,则第i个传感器量测方程为
Zic(k)=Hi(k)![]() (k)+ui(k) (3)
(k)+ui(k) (3)
其中ui(k)是均匀分布的随机变量,![]() (k)是目标的预测值.对这些杂波作如下假设:(1)杂波在观测空间中均匀分布,(2)杂波测量相互独立.
(k)是目标的预测值.对这些杂波作如下假设:(1)杂波在观测空间中均匀分布,(2)杂波测量相互独立.
第i个传感器在k时刻得到的一组有效量测为
Zi(k)={Zij(k)},j=1,2,…,mk (4)
在论域Zi(k)={Zij(k)}上,“某一量测可能来自目标”所构成的模糊集合Ai的关联矩阵为(设目标数为1)
μiA={μiA(Zij(k))}1×mk (5)
μiA(Zij(k))反映了目标和第j个量测之间的模糊关联度.于是,一旦得到一组量测,就查得到一组模糊信息Ai.由估计理论和模糊系统理论,可得到如下模糊最小方差估计.
设参数集合X={X1,X2,…,Xm}为要估计的参数.若所得到的估计量![]() ij使估计的均方误差最小,则称
ij使估计的均方误差最小,则称![]() ij为模糊最小方差估计.
ij为模糊最小方差估计.
J=E{(Xj-![]() ij)(Xj-
ij)(Xj-![]() ij)}=∫(Xj-
ij)}=∫(Xj-![]() ij).(Xj-
ij).(Xj-![]() ij)P(Xj|A)dXj (6)
ij)P(Xj|A)dXj (6)
![]() ij应使J达到极小.其中
ij应使J达到极小.其中![]() ij是基于模糊信息Ai对Xj的估计,它是Ai的函数.令g(Ai)=
ij是基于模糊信息Ai对Xj的估计,它是Ai的函数.令g(Ai)=![]() ij.则
ij.则
J=E{(Xj-g(Ai))T(Xj-g(Ai))} (7)
在上式中两边对g(Ai)求导,并令其为零,可得
![]() ij=g(Ai)=E[Xj|Ai]=∫XjP(Xj|Ai)dXj (8)
ij=g(Ai)=E[Xj|Ai]=∫XjP(Xj|Ai)dXj (8)
为方便起见,略去下标j,目标在k时刻,第i个传感器的状态估计可以写成如下形式
![]() i(k/k)=∫X(k)P(X(k)|Ai,Zi,k-1)dX(k) (9)
i(k/k)=∫X(k)P(X(k)|Ai,Zi,k-1)dX(k) (9)
其中Zi,k-1={Zi(n)}k-1n=1表示第i个传感器直到时刻k-1的累积量测集.式(9)的离散形式为
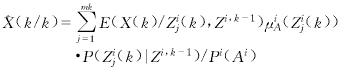 (10)
(10)![]() (11)
(11)
令 Wij(k)=μiA(Zij(k))P(Zij(k)|Zi,k-1)/Pi(Ai) (12)
称Wij(k)为加权系数.则式(10)可写为
![]() (13)
(13)
假设X(k)是正态分布,则由Kalman滤波器得
![]() (14)
(14)
估计误差协方差矩阵为
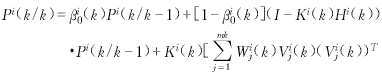
-Vi(k)(Vi(k))T](Ki(k))T (15)
Pi(k+1/k)=Φ(k)Pi(k/k)ΦT(k)+Q(k) (16)![]() (17)
(17)
Vij(k)=Zij(k)-Hi(k)Xi(k/k-1) (18)
Ki(k)=Pi(k/k-1)(Hi(k))T[Si(k)]-1 (19)
Si(k)=Hi(k)Pi(k/k-1)(Hi(k))T+Ri(k) (20)
其中βi0(k)是跟踪门设有一个测量来自于被跟踪目标的概率,其算式下一节给出.目标状态的多传感器估计为
![]() (k/k)=∫X(k)P(X(k)/A,Z1,k-1,…,Zn,k-1)dX(k) (21)
(k/k)=∫X(k)P(X(k)/A,Z1,k-1,…,Zn,k-1)dX(k) (21)
为简化起见,我们仅考虑两个传感器的情形,对![]() (k/k)的序列估计方法如下.
(k/k)的序列估计方法如下.
(1)预测 基于![]() (k-1/k-1)和它的协方差P(k-1/k-1),分别应用以下各式计算预测的状态
(k-1/k-1)和它的协方差P(k-1/k-1),分别应用以下各式计算预测的状态![]() (k/k-1)和它的协方差P(k/k-1),以及预测的量测Z1(k)和相应的协方差S1(k).
(k/k-1)和它的协方差P(k/k-1),以及预测的量测Z1(k)和相应的协方差S1(k).
![]() (k/k-1)=Φ(k-1)
(k/k-1)=Φ(k-1)![]() (k-1/k-1) (22)
(k-1/k-1) (22)
P(k/k-1)=Φ(k-1)P(k-1/k-1)ΦT(k-1)+Q(k-1) (23)
Z1(k)=H1(k)![]() (k/k-1) (24)
(k/k-1) (24)
S1(k)=H1(k)P(k/k-1)(H1(k))T+R1(k) (25)
(2)对第一个传感器确认量测 用Z1(k),S1(k)按照下式确认量测
(V1j(k))T[S1(k)]-1V1j(k)<γ1 (26)
其中V1j(k)=Z1j(k)-Z1(k).γ1为第一个传感器的跟踪门的门限值.
(3)用第一个传感器确认的量测进行状态估计
![]() (27)
(27)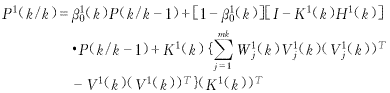 (28)
(28)
(4)对第二个传感器确认量测 基于![]() (k/k)和P1(k/k),按照下式确认量测.
(k/k)和P1(k/k),按照下式确认量测.
Z2(k)=H2(k)![]() 1(k/k) (29)
1(k/k) (29)
S2(k)=H2(k)P1(k/k)(H2(k))T+R2(k) (30)
(V2j(k))T[S2(k)]-1V2j(k)<γ2 (31)
其中V2j(k)=Z2j(k)-Z2(k).γ2为第二个传感器的跟踪门的门限值.
(5)用第二个传感器确认的量测计算状态估计和它的协方差,且作为多传感器的状态估计和它的协方差
![]() (32)
(32)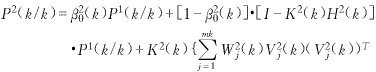
-V2(k)(V2(k))T}(K2(k))T (33)
令 ![]() (k/k)=
(k/k)=![]() 2(k/k),P(k/k)=P2(k/k)
2(k/k),P(k/k)=P2(k/k)
三、对加权系数Wj(k)的分析
为简化起见,省去式(12)中的i标注.式中的μA(Zj(k))表示第j个量测与目标航迹间的模糊关联度.P(Zj(k)/Zk-1)表示第j个量测与目标航迹之间的关联概率.P(A)为归一化系数.可见,加权系数Wj(k)实际上由模糊关联度和关联概率共同组成.
令 μj(k)=μA(Zj(k));βj(k)=P(Zj(k)/Zk-1).
则 Wj(k)=μj(k).βj(k)/P(A) (34)
μj(k)的求法在下一节给出;βj(k)的求法已在文献[3]中给出.
![]() (35)
(35)![]() (36)
(36)
其中ei(k)=exp{-(Vi(k))TS-1(k)Vi(k)};
b(k)=λ|2πS(k)|1/2(1-PDPG)/PD.
PG为正确测量落入跟踪门的概率,PD为正确测量的检测概率,λ为杂波密度.为简化起见,本文假设PD=PG=1.
进一步研究发现,在目标的匀速和匀加速运动段,PDAF可以较好地解决数据关联问题.当目标发生强机动时,由于密集杂波干扰,真实目标回波的新息Vj(k)增大,关联概率βj(k)减小.这将进一步使新息Vj(k)增大,关联概率βj(k)减小,最终导致关联失败,目标丢失,如图1所示.因此,当目标发生强机动时,单用PDAF方法将容易丢失目标.而在这种情况下,基于目标的机动特征,模糊逻辑关联方法却可以较好地解决目标的数据关联问题.所以,在目标不同的运动段,模糊关联度μj(k)和关联概率βj(k)应有不同的侧重,两者交互作用,充分发挥各自的优势,使系统的关联性能达到最佳.
模糊关联度μj(k)和关联概率βj(k)相互切换的依据是判定目标的运动状况.本文采用如下方法[4]检测目标的运动状况;首先,计算各时刻的所有有效回波新息之和![]() (k).其次,取一个长度为L的滑窗,滑窗内新息序列
(k).其次,取一个长度为L的滑窗,滑窗内新息序列![]() (k)的总和定义为:
(k)的总和定义为:
![]() (37)
(37)
根据统计量DL(k),用公式表示假设检验问题.在H0假设下,无机动目标时,DL(k)呈正态分布,其均值趋于零,方差为:
![]() (38)
(38)
式中s(i|i-1)为![]() (i)的方差.如果H1假设成立,即目标出现机动,DL(k)就呈非零均值的正态分布,但方差仍与式(38)中的相同.其均值由下式给出:
(i)的方差.如果H1假设成立,即目标出现机动,DL(k)就呈非零均值的正态分布,但方差仍与式(38)中的相同.其均值由下式给出:
![]() (39)
(39)
式中![]() ,
,![]() m(i)为机动模型下的滑窗内新息序列.最佳Neyman-Pearson检验由如下似然比确定.
m(i)为机动模型下的滑窗内新息序列.最佳Neyman-Pearson检验由如下似然比确定.
![]() (40)
(40)
对上式两边取对数,得
![]() (41)
(41)
用两个高斯概率密度代替P(DL(k)|H1)和P(DL(k)|H0),可得到
![]() (42)
(42)
选择门限(k)以满足由下式给出的特定虚警率:
Pf=∫∞γ(k)N(a;m,σ2L(k))dα (43)
式中的N(α;m,σ2L(k))表示均值为m,方差为σL的高斯概率密度函数.门限?(k)为
?(k)=σ2L(k)erf1(1-pf) (44)
式中 erf1(u)=∫u-∞N(α;0,1)dα.当目标发生机动时,DL(k)的期望值将逐渐增大.因此,在系统规定的虚警率下,由Neyman-Pearson准则可确定出一门限.将DL(k)与该门限值比较来判定目标的运动状况.
如果将上述的模糊-概率数据关联算法与多模型算法相结合,将会得到更好的跟踪性能.文献[5]中给出了完整的多传感器相互作用多模型-模糊,概率数据关联算法及分析.该算法能够实现的关键步骤是给出了多模型概率之间的相互转换计算式:
![]() (45)
(45)
其中c为归一化系数,![]() ,Λj(k)为似然函数.它的计算式如下
,Λj(k)为似然函数.它的计算式如下
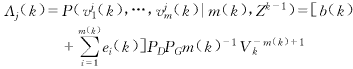 (46)
(46)
式中各参量的定义与式(36)的相同.可见,似然函数是新息的联合概率密度函数.新息自然是模型之间转换的主要依据.从而确定出模糊关联度μj(k)和关联概率βj(k)的作用期.
四、模糊关联度μ(k)的计算
应用模糊逻辑推理系统[6]来求模糊关联度.该模糊关联系统包含四个基本单元:模糊化界面,模糊知识库,模糊推理机和去模糊界面.以各回波的新息范数,即
gi(k)=VTi(k)S-1(k)Vi(k) (47)
和滑窗内新息序列![]() (k)的总和DL(k),作为模糊关联系统的输入特征量.因为,当目标出现机动时,真实目标的新息范数gi(k)和DL(k)都将明显增大.而杂波的新息范数没有这种特征.系统的输出量为模糊关联度.由于受虚警率,滑窗长度,机动量及噪声水平等多种因素的影响,输入量与输出量之间的映射关系是非线性的.经过适当的训练,该模糊系统可得到如下形式的M条推理规则:
(k)的总和DL(k),作为模糊关联系统的输入特征量.因为,当目标出现机动时,真实目标的新息范数gi(k)和DL(k)都将明显增大.而杂波的新息范数没有这种特征.系统的输出量为模糊关联度.由于受虚警率,滑窗长度,机动量及噪声水平等多种因素的影响,输入量与输出量之间的映射关系是非线性的.经过适当的训练,该模糊系统可得到如下形式的M条推理规则:
Rj:IF y1 is Aj1 and y2 is Aj2 Then Z is Bj,j=1,2,…,M (48)
其中Aji和Bj分别为用模糊隶属函数μjAi(yi)和μjB(Z)表示的语义项.设A′y是输入论域U中的任意模糊集;则式(48)的每一条规则Rj可用取大-星乘合成算子Sup-star composition确定输出论域V中的模糊集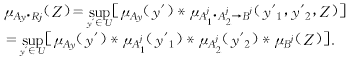
最后,由重心去模糊算法得出关联度
![]()
其中![]() j是μBj(Z)达最大值的点.
j是μBj(Z)达最大值的点.
模糊系统的学习算法有多种[6],但它们都是基于半模糊模型,即前提的模糊隶属函数为单值.单值模糊产生方法不适合含有噪声的情况.作者在文献[5]中采用了一种基于最陡下降法的全模糊模型学习算法,可用于受噪声影响的模糊关联系统的学习.
五、仿真举例
1.航迹模型
该机动目标的航迹由三个不同的运动段组成.第一段为匀速运动段,沿X轴方向,起始于点x=0,y=5km,vx=0.5km/s,vy=0,持续1~50秒.第二阶段为加速转弯段,加速度为ay=5g,ax=0,持续51~70秒.第三阶段为匀速运动段,沿Y轴方向,vy=0.5km/s,vx=0,持续71~100秒.假设每个采样点上,有效杂波回波数为2个.采样间隔T=1s.
2.性能检验与比较
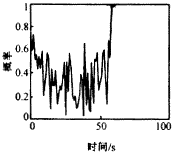
首先,考虑用PDAF和多模型方法共同作用的情况.图1给出了所得到的跟踪结果.可见,当机动发生时,由于密集杂波的干扰,造成关联错误,导致目标丢失.图2,3分别给出了上述情况时,各有效回波源于目标的概率.可见,当机动发生时,真实目标回波的概率趋于零.而杂波的概率却趋于1.
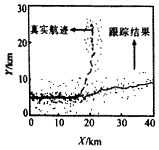
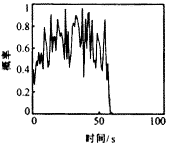
|
图1 用PDAF得出的跟踪结果 |
图2 真实目标回波的关联概率 |
|
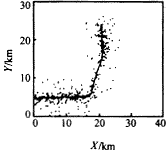
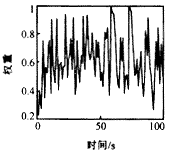
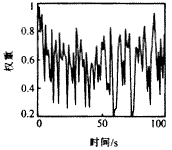
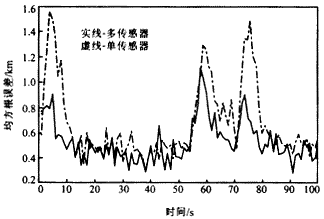
图3 杂波回波的关联概率 其次,考虑用本文提出的模糊逻辑和概率交互作用的数据关联方法与多模型方法共同作用的情况.经Monte Carlo仿真,得如下结果.图4给出了跟踪结果.可见,较好地实现了对该机动目标的跟踪.图5,6分别给出了上述情况时,各有效回波的加权系数.可见,真实目标回波的加权系数明显大于杂波的权系数.最后,考虑分别使用多传感器和单传感器时,目标状态估计精度上的差异.图7给出了上述两种情况时的目标位置估计的均方误差.可见,多传感器的估计精度明显好于单传感器时的估计精度,尤其是在机动发生处. |
|
图4 用本文算法得出的跟踪结果 |
图5 真实目标回波的加权系数 |
|
图6 杂波回波的加权系数 |
图7 用多传感器和单传感器分别所得目标位置估计的均方概误差 |
| 六、结 论 本文首先分析了在密集杂波干扰环境中,使用PDAF方法存在的不足.然后,基于估计理论和模糊系统理论,给出了多传感器模糊滤波算法以及模糊逻辑和概率交互作用的数据关联算法.模糊关联度和关联概率共同组成了各有效回波的加权系数.两者在目标的不同运动段,有不同的作用期,相互补充,充分发挥各自的优势,明显提高了系统的数据关联性能.模糊关联系统由适合于噪声影响的全模糊模型构成,其模糊隶属度函数可由基于最陡下降法的自学习算法来决定.多传感器的目标状态估计由多传感器序列估计算法实现.仿真结果充分证明了,本算法解决在密集杂波干扰环境下多传感器跟踪机动目标的数据关联问题的有效性,以及多传感器对目标状态估计精度的有效改善.本文算法的重要理论贡献在于首次给出了多传感器模糊逻辑关联算法和概率数据关联算法融合在一起作用的解析式.解决了长期以来各自独立发展,独自应用,各受局限的问题.对多传感器多回波目标跟踪理论的发展具有重要意义. |
 电子发烧友App
电子发烧友App






















评论