Matlab源程序 - RBF神经网络在智能传感器模块设计中的应用

RBF神经网络Matlab源程序如下：

clc

clear

close all %程序开始前，清屏，清除其它变量

%输入原始数据，每一列为一个变量，行数为样本的个数。原始标定数据的输入，可以将数据直接输入至程序中，也可以将数据先输入至文件，然后在程序中读入数据文件。数据中的P、Ut、Ui、Up均为维列向量， 为标定数据点的个数

raw_data=[P Ut Ui Up]； %学习（训练）样本

data_test=[P_test Ut_test Ui_test Up_test]； %测试样本

%根据原始数据制作学习（训练）样本与测试样本，学习样本与测试样本的数据格式相同

P=raw_data(: , 1); Ui=raw_data(: , 2); Ut=raw_data(: , 3); Up=raw_data(: , 4);

P_test=data_test(: , 1); Ui=data_test(: , 2); Ut=data_test(: , 3); Up=data_test(: , 4);

P1= ; [Up Ui Ut] %学习样本输入

T1= ; P' %学习样本期望输出

P2= ;[Up_test Ui _test Ut_t est]' %测试样本输入

T2=P_test' ； %测试样本输出

%将输入数据进行归一化

[PN1，Minp，maxp，TN1，mint，maxt]=premnmx(P1，T1)；

PN2=tramnmx(P2，minp，maxp)；

TN2=tramnmx(T2,mint,maxt);

%训练

switch 2

case 1 %神经元数是训练样本个数

spread=0.1； %此值越大，覆盖的函数数值就越大（默认为1）

net=newrbe(PN1，TN1，spread)；

case 2 %神经元数逐步增加，最多就是训练样本个数

goal=1e－8； %训练误差的平方和（默认为0）

spread=0.1； %此值越大，需要的神经元就越少（默认为1）

MN=size(PN1,2)； %最大神经元数（默认为训练样本个数）

DF=2； %显示间隔（默认为25）

net=newrb(PN1，TN1，goal，spread，MN，DF);

case 3

spread=0.1； %此值越大，需要的神经元就越少（默认为1）

net=newgrnn(PN1，TN1，spread);

end

%测试

YN1=sim(net，PN1)； %学习（训练）样本实际输出

YN2=sim(net，PN2)； %测试样本实际输出

MSE1=mean((TN1－YN1).ˆ2 %学习（训练）样本实际输出的均方误差

%n1=length(TN1)；%e1=sum((TN1－YN1).ˆ2/n1

%e1与MSE1相等

MSETD1=std((TN1－YN1).ˆ2

MSE2=mean((TN2－YN2).ˆ2 %测试样本实际输出均方误差

%n2=length(TN2)；%e2=sum((TN2－YN2).ˆ2/n2

%e2与MSE2相等

MSETD2=std((TN2－YN2).ˆ2

%反归一化

Y1=postmnmx (YN1,mint,maxt)' %将归一化的学习（训练）输出数据恢复为原始数据

E1=Y1－P %学习（训练）输出数据与标定值之间的偏差

Y2=postmnmx (YN2,mint,maxt)' %将归一化的测试输出数据恢复为原始数据

E2=Y2－P_test %测试输出数据与标定值之间的偏差

max(E2)

min(E2)

采用经过数据归一化处理的程序

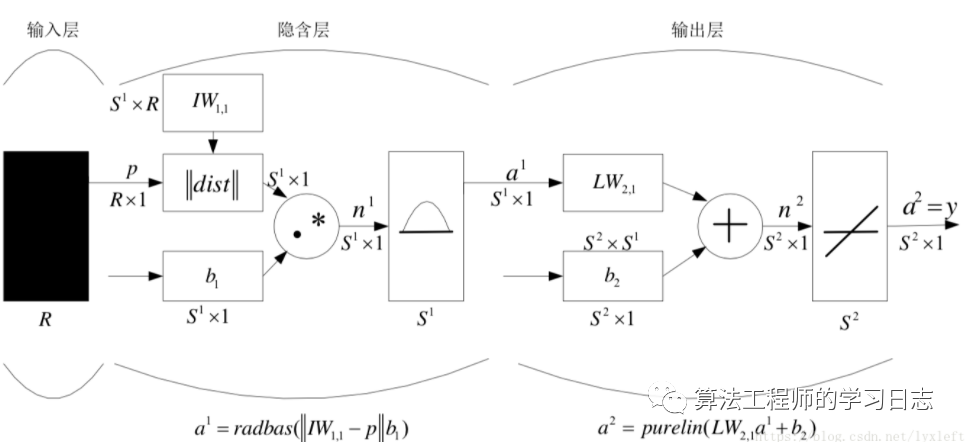
神经网络采用Matlab中的newrb()函数，neurons=252。学习样本经RBF神经网络训练后的输出值与相应的压力标定值之间的最大误差绝对值为1.0396e－011，均方误差MSE1=5.6613e－023，均方误差的标准差MSETD1=2.4666e－022。这里省略学习样本的预测输出表。可见，采用RBF神经网络对学习样本的输出已经消除了压力传感器的交叉敏感影响（在误差允许的范围内）。

检验样本经RBF神经网络的输出值与相应的压力标定值之间最大偏差绝对值为max=0.0113，均方误差MSE2=3.8568e－005，均方误差的标准差MSETD2=2.1727e－004。输出样本的详细情况见表5（只列出部分数据）。

数据融合效果评价

降低温度与电源波动两个干扰量的影响，传感器系统稳定性的改善程度分别用融合前后的零位、灵敏度温度系数以及电流影响系数来评价。

由于学习（训练）样本的网络输出值与标定值之间的偏差很小（均小于1.0e－011），如果根据这些数据来计算融合后的效果，可以认为已经完全消除交叉敏感。通过表5可知，本例中检验样本的网络输出值与标定值之间的偏差与学习样本的偏差相比，偏差较大，故按检验样本计算出数值来评价数据融合效果。

表5 输出样本

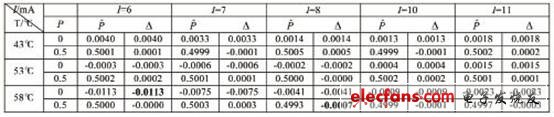
注：表中T表示工作温度，I表示工作电流，P表示压力标定值，表示压力计算值，偏差，单位都是V。

融合前：满量程输出值UFS=4.928V，当温度的变化范围为=39℃（由25℃至64℃），电流由6mA至11mA，变动时，零点值的最大变化范围=0.356V（由0.328V至-0.028V），满量程输出值由4.928V下降到2.710V，输出变化范围=-2.218V。

（1）零位温度系数

（2）灵敏度温度系数

（3）电流影响系数

利用检验样本计算的融合后的零位温度系数、灵敏度温度系数以及电流影响系数如下：

在=39℃，变化范围内，零点融合计算值的最大偏差 =0.0113MPa；满量程压力PFS=0.5MPa，其融合计算值的最大偏差量=0.0007MPa，则有

将融合前和RBF神经网络融合后的各参数列于表6中。

表6 融合前和RBF神经网络融合后的各参数

从表6可见，经RBF神经网络融合后，零位温度系数降低到融合前的1/3，灵敏度温度系数降低约3个数量级，电流影响系数降低约2个数量级

结束语

由于半导体的特性参数易受温度、电流的影响而变化，压阻式传感器将会产生很大的零位温度漂移、灵敏度温度漂移和电流影响漂移，这是压阻式传感器最大的弱点。因此，研究改善压阻式压力传感器的温度稳定性与恒流源供电电流的稳定性，在生产实践中很有意义。采用RBF神经网络法，设计了抗两个干扰量影响的智能化软件模块，对压阻式压力传感器稳定性进行改善，取得了很好的效果。该方法简单易行，精度较高，将压阻式压力传感器输出精度控制在0.01%以内。