- 比率传感器的基本原理及与模数转换器ADC的配合使用方法解析

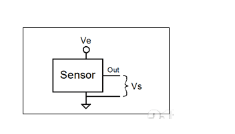
由图6可以得出下列公式：

Vs = （V+） x Rt/（R1+R2+Rt） 公式12

Vref = （V+） x R1/（R1+R2+Rt） 公式13

将公式12中的Vs和公式13中的Vref代入公式4，得出图6中ADC的输出。经过简化可得公式14。公式14表示：如果R1是定值，D则正比于、且仅随Rt的变化而变化，这正是所期望的结果。

D = FS x K x （Rt/R1） 公式14

由公式14 可以看出，R2不影响读数；R2降低了Rt所消耗的功率。如果没有R2的话，Rt的自身热量将导致温度示数出现很大误差。R2还降低了ADC的共模输入电压。这对某些共模输入电压范围小于电源电压的ADC是非常必要的。

类似于MAX1403的ADC包含用于驱动RTD的电流源。然而，它们并不是精密电流源，还需要进行一些校准。校准通常是采用一个额外的ADC输入来测量由相同的电流源驱动的参考电阻来实现的。然后，采用软件按照已知电阻的测量值依比例确定未知电阻的测量值。虽然这种技术可以很好地工作，不过，将R1作为参考电阻更加简单并且无需额外的ADC输入。板上的电流源仍能用来激励RTD和参考电阻。用一个电流源替换图6中的R2不会对公式14产生影响。

一些ADC可提供两个互相匹配的电流源用于精确测定远程RTD。在这些应用中长导线的电阻会增加RTD的阻抗，从而产生误差，必须想办法去除。成本最低的解决方案是采用三线RTD。如图7所示，电流源1可用于产生RTD两端的压降。该电流源还在通向RTD的上部导线上产生额外的压降。为了补偿这个多余的压降，用电流源2在中间的导线上产生一个压降。通过RTD底部的导线使这两个电流源流向地。RTD上三根导线的长度和材料都相同，这样可使彼此之间的电阻非常接近。匹配电阻传送匹配电流可产生匹配的压降。因此，上部的两根导线压降彼此抵消，ADC上的差分输入电压与RTD两端的电压相同。

图7. MAX1403 ADC有两个匹配的电流源，在该电路中，电流源1用于产生RTD两端的压降，电流源2用于产生中间导线的压降。

温度和压力
       图8结合了图5和图6中的设计理念，采用一个很简单的电路，以单个电阻作为基准同时测量温度和压力。Vs1和Vs2的幅值相差很大。这个差值可通过改变ADC （例如MAX1415）内置可编程增益放大器（PGA）的增益进行调节。这些转换器允许PGA对每个通道都设置不同的增益。增益的改变可使公式4中的K值改变，因此，允许单个参考电压能够适应较宽范围的输入电压。

图8. 用单个电阻作为基准的简单电路测量温度和压力

惠斯通电桥

      惠斯通电桥是由Charles Wheatstone爵士（1802至1875）在电子学发展的早期阶段发明的。惠斯通电桥通过对三个已知电阻值和一个未知电阻值进行比较来测量电阻。当电桥恰好达到平衡时，电阻测量值与激励电压、仪表精度或电路中的仪表负载无关。在尚不具备电压标准和高品质仪表的时代，这个条件是非常重要的。然而，桥式电路在当前仍很流行，因为在所有电桥电阻具有相同的温度系数时，它们不会产生大的失调并能抑制温度效应。

      图9是一个由同一电压源供电的两个分压器组成的惠斯通电桥。习惯将电桥画成菱形，因为这种形状强调了同一电压源为每个分压器供电的重要性。电桥的输出（Vo）是两个分压器输出电压之差（公式15）。当Vo为零时，称电桥达到平衡。在这种条件下，因为Ve与一个为零项相乘，所以激励电压（Ve）的精确值并不重要。公式16可计算出平衡电桥中未知电阻（Ru）的阻值。在实际应用中，通常使Ra = Rb，这样公式16可简化为Ru = Rc。

图9. 由同一个电压源供电的分压器组成的惠斯通电桥示意图

Vo = Vb（Rc/（Rc+Ru） - Rb/（Ra+Rb）） 公式15

若Vo = 0，则Ru = Rc x Ra/Rb 公式16

目前已经很少使用平衡电桥电路测量电阻，但是在传感器中采用非平衡电桥相当常见。在工厂校准时，电桥通常被平衡在一个优选的工作点上；通过测量电桥中的不平衡来测量与该点的偏差。下面举例说明以该方式使用电桥的优点。

假定将一个硅应力计与薄膜相粘合，构成一个压力传感器，并具有所期望的压力分辨率（0.1%）。在0psi和25°C条件下，电阻的阻值为5000Ω。在100psi （满量程压力）和25°C的条件下，电阻值增加2%，达到5100Ω。除了对应力敏感，电阻对温度也敏感，具有2000ppm/°C的电阻温度系数（TCR）。

由于在整个压力范围内电阻变化了100Ω，因此必须能够分辨0.1—＃937；的电阻才能获得0.1psi （0.1%）的压力分辨率。测量5000Ω中的0.1Ω相当于50，000分之一或15.6位的分辨率。比分辨率更严重的问题是温度变化的影响。由于电阻具有较高的TCR，温度每变化1°C，相当于压力变化10psi对电阻的影响。每摄氏度的温度变化对电阻的影响相当于满量程的10%。

现在考虑电桥电路中采用相同的电阻，激励电压为2V时的情况。其他三个电阻都是5000Ω，并和感应电阻具有相同的TCR。这些电阻的安装条件能够保证其等温。这种方式具有两个显著的优点。

该应用中电桥的最大优点是它能抑制温度引起的变化。分析公式15发现TCR不再是问题。即使电桥电阻加倍输出仍保持不变。只要所有电阻按同比例变化，其输出不变！

电桥的第二个优点是降低了分辨率要求。在压力为0psi时，电桥输出是0mV，在100psi时电桥输出为10mV。要测量0.1psi的压力，则需要从10mV中分辨10？V。相对于直接测量电阻需要15.6位的分辨率而言，只需要10位的分辨率。

从实际应用的角度来看，10位ADC不能直接测量10？V的信号。信号必须放大。信号放大的成本可能会使无需外部放大器的高分辨率ADC更吸引人。低分辨率方案的最大优点在于其对基准的要求。设计能在整个时间和温度范围内稳定达到16位分辨率的电压基准、电流源或参考电阻通常是不切实际的。

该实例中的数值选取不是用来刻意突出电桥的重要性。这些数值对于许多压阻式压力传感器非常典型（见附录2）。

惠斯通电桥的线性化

使用非平衡惠斯通电桥的缺点是其具有非线性。公式15分母中的Ru项表示：电桥的输出与Ru不是线性函数关系。电阻变化非常小时线性误差也很小，而当电桥不平衡时线性误差也变大。幸运的是，如果ADC参考电压来自电桥的话，就可消除这个误差。

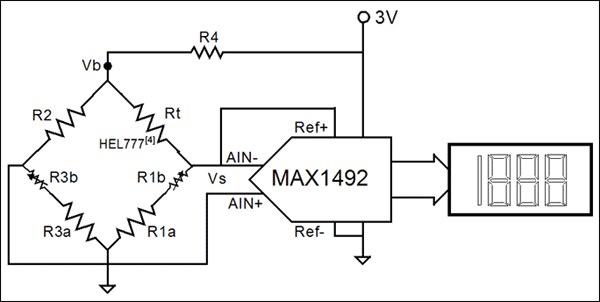
图10所示为一个带数字显示的简单温度传感器。温度感应元件（Rt）是铂RTD。选择铂是因为其电阻随温度线性变化。电桥电路除去0°时的多余信号，这样可使ADC的读数等于温度。公式17给出了图10中的电桥信号（Vs）。公式18是ADC的参考电压。两信号都是Rt的非线性函数，但是它们共同作用的结果是线性的。

如何利用传感器和ADC的比率特性来提高电子系统的精度

图10. 在具有数字显示的简单的温度传感器中，电桥电路除去0°时的多余信号，使得ADC读数等于温度。

Vs = （Vb）（R3/（R2+R3） - （R1/（R1+Rt）） 公式17

Vfer = （Vb）（R1/（R1+Rt） 公式18

ADC的输出（公式19）是将公式17和18中的Vs和Vref分别代入公式4中得出的。公式19表示采用这个参考电压时，ADC输出变为Rt的线性函数，并减去所期望的偏移项。

D = Rt（R3/（R1（R2+R3）） - R2/（R2+R3） 公式19

在图10中，R3b和R1b分别调节失调量和灵敏度。当进行调节时，显示器将直接以°C或°F为单位显示温度的大小。唯一的一个明显误差来自RTD自身的非线性。0°C至100°C范围内该误差仅为十分之几摄氏度。

通过MAX1492 ADC的串行接口，还可对图10电路的失调误差和灵敏度误差进行数字校正。这种校准方法不仅无需R1a和R3a，而且还提供了校正RTD中线性误差的机会。如果需要更高的测量分辨率，可用MAX1494替换MAX1492，可使分辨率上升一位。

根据公式19，R4的值不会影响读数。电路中增加R4可以降低RTD的自身热量。同时也减弱了来自电桥的信号，并且降低了参考电压。虽然MAX1492无内部PGA，但是它允许使用较小的参考电压。使用较小的参考电压可以省去额外的放大电路。

结束语

在许多传感器应用中，利用简单电路，使传感器输出和ADC参考输入之间保持适当的关系，可以省去电压基准和电流源。除了降低成本和节省空间之外，这些电路还可消除不理想基准所引入的误差，改善性能。