磁通定理_磁通密度计算公式_变压器空载运行的磁通和感应电动势

　　表示磁场分布情况的物理量。通过磁场中某处的面元dS的磁通量dΦ定义为该处磁感应强度的大小B与dS在垂直于B方向的投影dScosθ的乘积，即dFB =BdScosθ式中θ是面元的法线方向n与磁感应强度B的夹角。磁通量是标量，θ《90°为正值，θ》90°为负值。通过任意闭合曲面的磁通量 ΦB 等于通过构成它的那些面元的磁通量的代数和，即对于闭合曲面，通常取它的外法线矢量（指向外部空间）为正。上篇中提到感应电动势的计算公式（感应电动势是什么_感应电动势公式_感应电动势的计算）这篇小编要讲磁通定理，看看变压器空载运行的磁通和感应电动势会发生什么？

　　什么是磁通

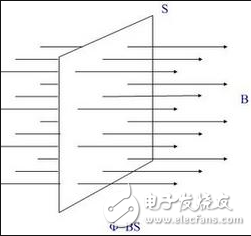
　　垂直穿过某一截面S的磁力线总数称为磁通。

　　磁感应强度B与垂直于磁场方向S的乘积，称为通过该面积的磁通，即φ=BS

　　磁通的单位为韦伯（Wb）

　　若磁场中各点的磁感应强度相等则为均匀磁场。

　　磁通定理

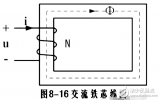
　　如果在磁场中任取一闭合面 ，规定外法线为正，则穿出闭合面的磁通量为正，穿入闭合面的磁通量为负。由于磁感应线是无头无尾的闭合线，有几根磁感应线穿入闭合面，一定有同样数目的磁感应线穿出闭合面。所以，通过任意闭合面的磁通量恒等于零。这就是磁通定理，其数学表达式为

　　磁通定理与静电场的高斯定理在数学表达式上相似，但它们在本质上不同，分别反映磁场和静电场（从磁感应线和电力线）在本质上的不同。上式可以从毕 - 萨定律出发加以严格证明。

　　磁通密度计算公式

　　定义：在均匀磁场中，磁感应强度B和垂直于磁场方向的某一面积S的乘积，称为通过这个面积的磁通量，用符号“Φ”表示。

　　因此可得知磁通量计算公式为：

　　上述公式中所代表的的具体含义分别是：

　　B：表示磁感应强度，单位（T）

　　S：表示与磁力线方向垂直的面积，单位（m2）

　　Φ：表示穿过S面积的磁通，单位（Wb）

　　磁通量单位：磁通量标示符Φ的国际单位制单位是韦伯，常以符号Wb表示。在电力工程计算中，也常采用麦克斯韦作单位，简称“麦”，韦伯和麦克斯韦之间的换算关系为：

　　1麦克斯韦（Mx）= 1 高斯（Gs）×厘米2 = 10-8韦伯（Wb）

　　磁通密度

　　如果吧磁感应强度B的大小和磁通量Φ与磁力线抽象的联系起来，则可认为磁通Φ在数值上就等于垂直通过该单位截面的磁力线条数。由磁通量计算公式Φ=BS得：

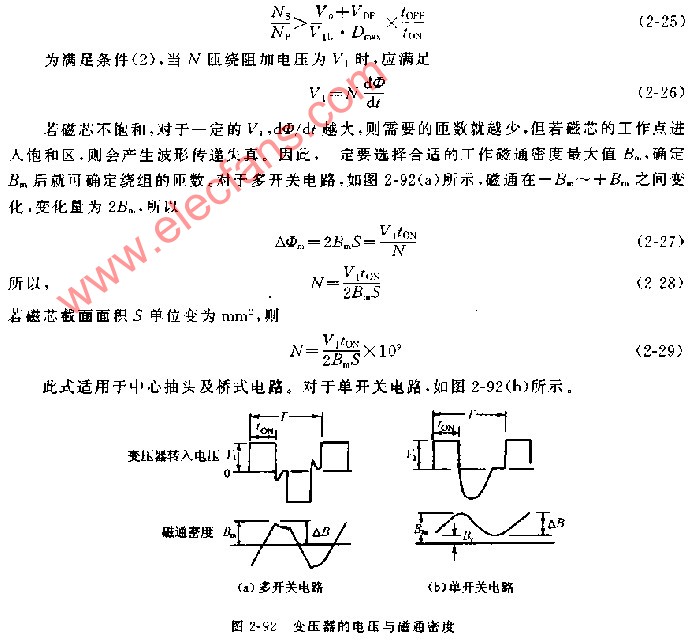
　　这样，磁感应强度B的大小就等于通过单位面积上的磁力线条数。因此，磁感应强度大小又称为磁通密度。由此得出一个结论：磁通密度是磁感应强度的一个别名，它表示垂直穿过单位面积的磁力线的多少。（注意笔者上面将Φ和B比作磁力线的描述中加粗的字体含义区别）

　　由此可知，B和Φ是从不同角度描述磁场性质的物理量。磁感应强度B是描述磁场中某点的磁场大小，而磁通量Φ是表示磁场中某一范围内的磁场总体情况的物理量。磁感应强度B是矢量（有大小和方向的量叫矢量），而Φ是标量（只有大小而无方向的量叫标量）。在分析电磁现象时，应视具体情况而选用合适的量。

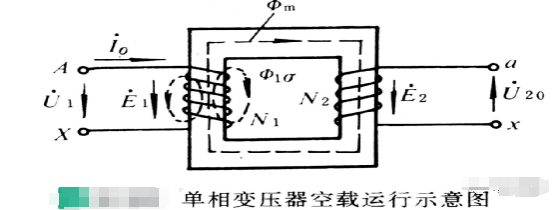
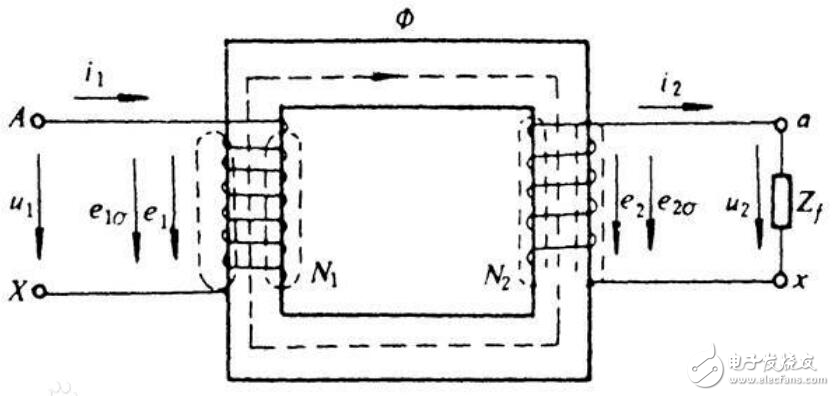
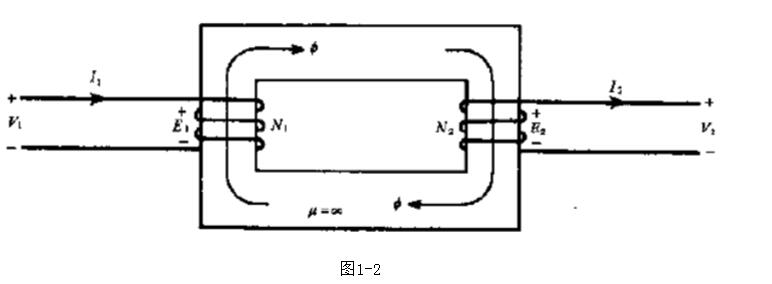
　　变压器空载运行的磁通和感应电动势

　　空载运行：是指变压器一次侧绕组接到额定电压、额定频率的电源上，二次侧绕组开路时的运行状态。

　　物理现象：

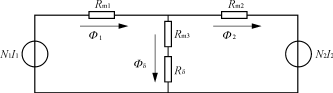
　　磁动势和磁通的情况：

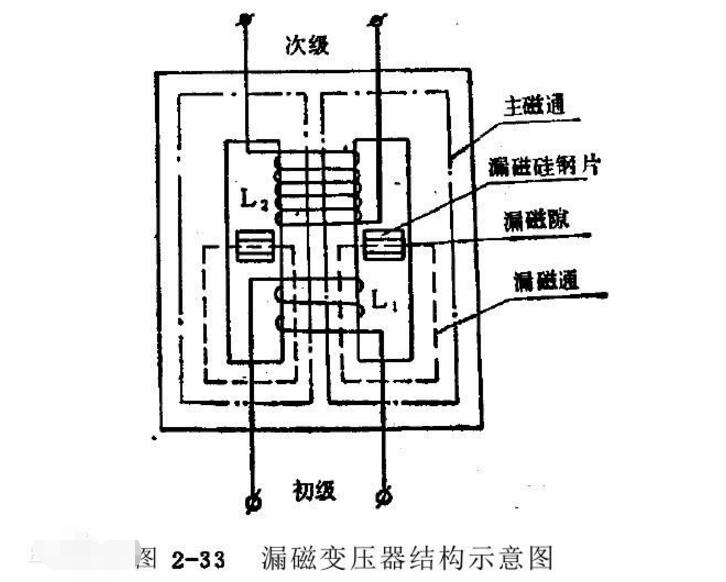
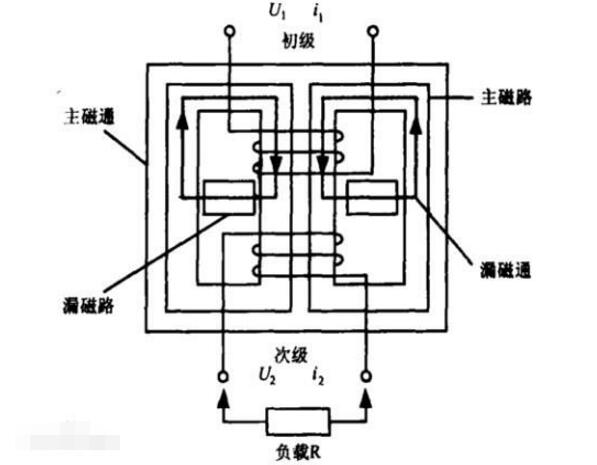
　　主磁通和漏磁通的区别：

　　1、由于铁磁材料有饱和现象，所以主磁路的磁阻不是常数，主磁通与建立它的电流之间呈非线性关系。而漏磁通的磁路大部分是非铁磁材料组成，所以漏磁路的磁阻基本上是常数，漏磁通与产生它的电流呈线性关系。

　　2、主磁通在一次侧、二次侧绕组中均感应电动势，当二次侧接上负载时便有电功率向负载输出，故主磁通起传递能量的作用。而漏磁通仅在一次侧绕组中感应电动势，不能传递能量，仅起压降作用。因此，在分析变压器和交流电机时常将主磁通和漏磁通分开处理。

　　正方向的规定

　　为什么要规定正方向？

　　1、根据电路的定律、定理，列出物理量间相互关系的代数表达式；

　　2、根据计算结果确定实际方向：

　　若计算结果为正，则实际方向与参考方向一致；

　　若计算结果为负，则实际方向与参考方向相反。

　　从理论上讲，正方向可以任意选择，因各物理量的变化规律是一定的，并不依正方向的选择不同而改变。

　　正方向规定不同，列出的电磁方程式和绘制的相量图也不同。在电机方向的学科中通常按电工惯例来规定正方向。

　　在负载支路，电流的正方向与电压降的正方向一致，而在电源支路，电流的正方向与电动势的正方向一致；

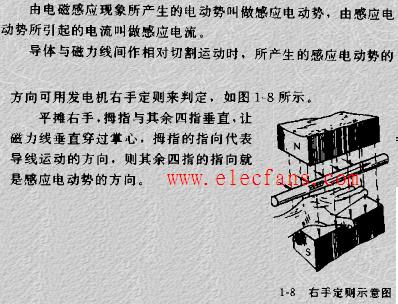
　　磁通的正方向与产生它的电流的正方向符合右手螺旋定则；

　　感应电动势的正方向与产生它的磁通的正方向符合右手螺旋定则；

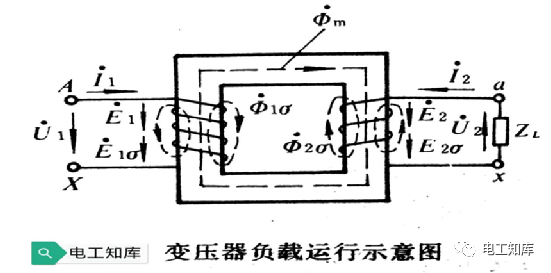
　　在一次侧，u1由首端指向末端，i1（i0）从首端流入。当u1与i1同时为正或同时为负时，表示电功率从一次侧输入，称为电动机惯例。在二次侧，u2和i2的正方向是由e2的正方向决定的，即i2沿e2的正方向流出。当u2和i2同时为正或同时为负时，电功率从二次侧输出，称为发电机惯例。

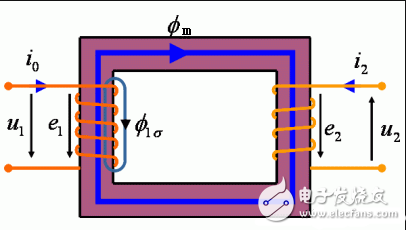
　　图 3．1 变压器的空载运行

　　空载时的电磁关系

　　电动势与磁通的关系：

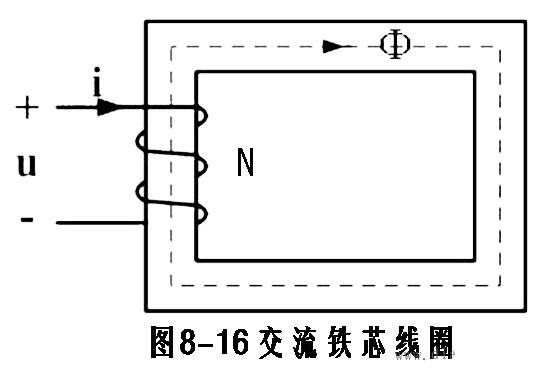
　　假定主磁通按正弦规律变化，即Φ=Φmsinωt

　　根据电磁感应定律和对正方向规定，一、二次绕组中感应电动势的瞬时值为 ：

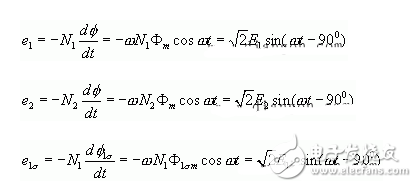
　　式中：