补码加法,补码加法计算原理
补码加法,补码加法计算原理
负数用补码表示后,可以和正数一样来处理。这样,运算器里只需要一个加法器就可以了,不必为了负数的加法运算,再配一个减法器。
补码加法的公式是
[x]补+[y]补=[x+y]补 (mod 2) (2.17)
现分四种情况来证明。假设采用定点小数表示,因此证明的先决条件是
︱x︱﹤1, ︱y︱﹤1, ︱x+y︱﹤1。
(1)x﹥0,y﹥0,则x+y﹥0。
相加两数都是正数,故其和也一定是正数。正数的补码和原码是一样的,可得:
[x]补+[y]补=x+y=[x+y]补 (mod 2)
(2)x﹥0,y﹤0,则x+y>0或x+y<0。
相加的两数一个为正,一个为负,因此相加结果有正、负两种可能。根据补码定义,
∵ [x]补=x, [y]补=2+y
∴ [x]补+[y]补=x+2+y=2+(x+y)
当x+y>0时,2 + (x+y) > 2,进位2必丢失,又因(x+y)>0,
故 [x]补+[y]补=x+y=[x+y]补 (mod 2)
当x+y<0时,2 + (x+y) < 2,又因(x+y)<0,
故 [x]补+[y]补=2+(x+y)=[x+y]补 (mod 2)
(3)x<0,y>0,则x+y>0或 x+y<0。
这种情况和第2种情况一样,把x和y的位置对调即得证。
(4)x<0,y<0,则x+y<0。
相加两数都是负数,则其和也一定是负数。
∵ [x]补=2+x, [y]补=2+y
∴ [x]补+[y]补=2+x+2+y=2+(2+x+y)
上式右边分为“2”和(2+x+y)两部分.既然(x+y)是负数,而其绝对值又小于1,那么(2+x+y)就一定是小于2而大于1的数,进位“2”必丢失.又因(x+y)<0,所以
[x]补+[y]补=2+(x+y)=[x+y]补 (mod 2)
至此我们证明了,在模2意义下,任意两数的补码之和等于该两数之和的补码.这是补码加法的理论基础,其结论也适用于定点整数
[例8] x=0.1001, y=0.0101,求x+y。
[解:]
[x]补=0.1001,[y]补=0.0101
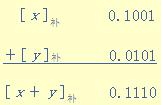
所以 x+y=+0.1110
[例9] x=+0.1011, y=-0.0101,求x+y。
[解:]
[x]补=0.1011,[y]补=1.1011
所以 x+y=0.0110
由以上两例看到,补码加法的特点,一是符号位要作为数的一部分一起参加运算,二是要在模2的意义下相加,即超过2的进位要丢掉。
非常好我支持^.^
(64) 17.5%
不好我反对
(301) 82.5%
相关阅读:
( 发表人:admin )
