零知识证明的逻辑概念详细解析

零知识证明的工程实现是一件极具挑战性的工作，但这并不意味着理解零知识证明这件事也同样困难，它背后的逻辑是简单的。

为什么需要去了解它？隐私问题自不用提，另一个重要原因则在于，随着对区块链探索的深入，我们发现通过密码学的方法来实现信任是对共识算法信任的有效补充，这两种信任可以更低摩擦地结合在一起，因此也更易被实现和应用。这个趋势也可以从近期区块链技术的发展方向中察觉到。

而只有当我们知道这些密码学方法背后的逻辑，才不会迷失其中，才能理解它为何要这样去设计，它适用于什么样的应用场景。

那么现在，就让我们开始零知识证明之旅吧。它包含三段旅程：

隐藏秘密之旅；

证明秘密之旅；

构建通用零知识证明之旅。

1. 隐藏秘密：单向功能

在《星际迷航》的宇宙中，P = NP，这对于计算界也许是件好事，它意味着所有可以在多项式时间内验证的问题，也可以在多项式时间内求解。但对于密码学界而言，这可能是一场灾难。

密码学需要存在一种「单向功能」，也就是说能够从 A 计算出 B，但从 B 计算出 A 存在着计算上的不可行性——计算从 A 到 B 是单向的，我们才有可能把 A 藏起来。而如果 P = NP，在多项式时间内可验证的问题同时也是可求解的，那么通过 B 就能计算出 A，秘密也就无法隐藏。

这就是密码学背后的简单逻辑：单向功能。而单向功能背后的支撑是 P！ = NP。

这与零知识证明的关系是什么呢？我们可以把零知识证明分解为两个功能，第一个功能是隐藏秘密，第二个功能是证明自己有秘密。而隐藏秘密，如上文所述，就是找到一个具有单向功能的计算式。

零知识证明：

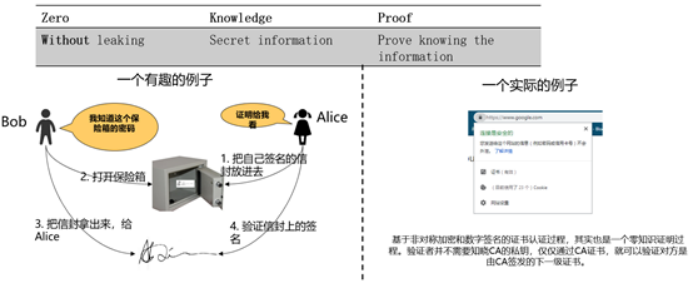
零知识证明是指让验证者相信某个断言为真，且整个过程不泄露「断言为真」之外的任何知识。为了更容易理解，本文把它简化为隐藏秘密和证明拥有秘密。

椭圆曲线算法（ECC）是密码学中被普遍应用的一个具有单向功能的函数，它看起来是这样的：k × P = Q，在已知 P 的情况下，我们可以通过 k 计算出 Q，但难以通过 Q 反向计算出 k。需要注意的是，密码学中加法或乘法运算的含义不局限于我们熟悉的实数域上加法或乘法运算的含义。

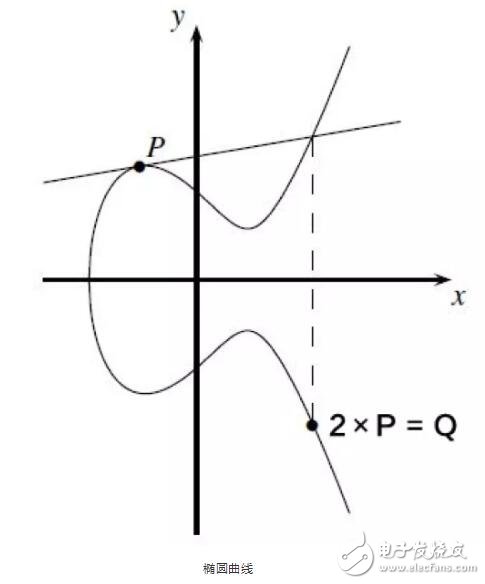
让我们看看它是如何做到单向性的。在该函数中，P 是椭圆曲线上的一个点，我们把一个小球放在该点并沿切线方向击打出去，小球在椭圆曲线中撞来撞去撞了 k 次（大致可以这么理解），最后会落在一个点 Q 上。如果我们知道初始位置 P 和撞击次数 k，是能算出小球的落点 Q 的；但如果我们只看见小球落在 Q 上，是无法算出从 P 点到 Q 点撞了多少次，也就是 k 的。

下图是 k = 2 的一个示例，小球从 P 点出发，撞击了两次落在 Q 点上，因此 Q 等于2 × P。椭圆曲线算法常被用于生成公钥和私钥，公钥就是小球最后的落点 Q，私钥就是撞击次数 k。k × P = Q 的单向功能使得它可以隐藏私钥这个秘密。

2. 证明秘密：同态

对于零知识证明来说，隐藏秘密只是第一步，我们还需要证明自己确实掌握了秘密。就像在第一段旅程中只需要理解单向功能，在这第二段旅程中，我们只需要理解「同态」，有了同态我们就有了证明秘密的能力。那么什么是同态？

我们可以把单向功能看成一种映射关系，比如 k × P = Q 就是 k 到 Q 的映射：在一个空间中，我们有无数个 k 点，它们被映射到另一个空间，变成无数个 Q 点。这就像现实世界和影子世界，通过光线的映射，现实空间的物体变成了影子空间的影子。

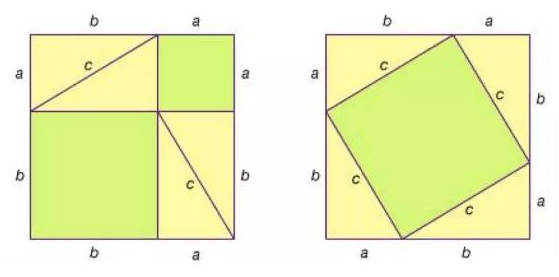
这时候假设有一块机械手表，机芯就是那个隐藏起来的秘密。我们把含机芯的手表拆成 8 个零部件并映射到影子空间中，这时影子空间就会有 8 个影子；但注意在现实空间我们展示给大家看的是一块完整的手表，机芯是未暴露的，这块手表在影子空间也会有个影子，我们叫它第 9 号影子。

现在我们把 8 个零部件的影子组合起来，如果它们能够组成一块完整的手表影子，就可以用该影子与第 9 号影子做对比，如果两者是相同的，就能证明现实空间的这块手表中是有机芯的，因为它的影子与含机芯的零部件组成的影子相同。这其实就完成了一个简单的零知识证明过程。

完整零部件的影子组合成的手表影子与完整手表的影子相同，我们称这种映射为同态。用数学公式来表达就是 f（手表） = f（零件1 + …… + 零件8） = f（零件1） + …… + f（零件8）。其中，f（手表）是手表的影子，f（零件1） + …… + f（零件8） 是零部件的影子组合成的手表影子。

简化一下这种关系就是：f（a+b） = f（a） + f（b），即「先计算后加密的结果」f（a+b） 与「先加密后计算的结果」f（a） + f（b） 是相同的。同态使得我们可以直接对密文进行计算，然后对隐藏了秘密的明文先计算后加密，再通过比较两者是否相同验证明文中是否真的藏有秘密。

同态定义：

抽象代数中，同态是两个代数结构（例如群、环、或者向量空间）之间的保持结构不变的映射。

如果你只想了解零知识证明的基本逻辑，旅程到这里就可以结束了，知识点只有两个：1. 用单向功能隐藏秘密；2. 用同态映射证明秘密。是不是还算轻松？

接下来让我们看看这个过程在真实的密码学中是怎样的，以椭圆曲线数字签名算法（ECDSA）为例，它是一个具有「零知属性」的算法。你可以选择不看，它不会影响你对同态的理解。

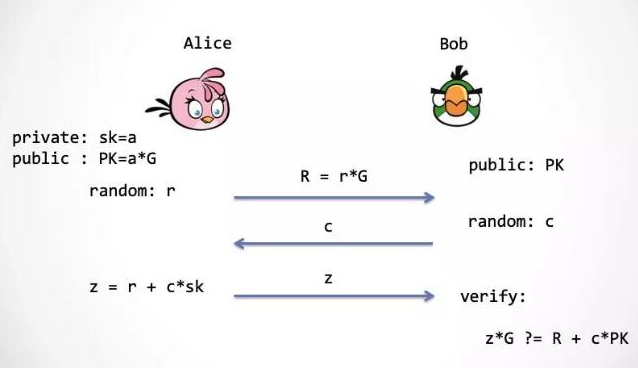
椭圆曲线数字签名算法对签名的验证：

在该算法中，关键的过程是验证 f（Z + dA × R） = f（Z） + f（dA × R） = f（Z） + Qa × R，其中，Z 是需要用私钥签名的消息，dA 是私钥，R 与随机数相关，Qa 是公钥。因为同态属性，这个等式是成立的，我们就可以用等式右边的 Qa（公钥）来验证 Z 是否是用等式左边的 dA（私钥） 签名的。

在这里，dA 是机芯，Z+dA×R 是藏有机芯的手表，f（Z + dA × R） 是这块手表的影子，而 f（Z） + f（dA × R） 是手表零部件的影子组合成的手表影子。

椭圆曲线算法的同态属性使得其他算法，比如椭圆曲线数字签名算法，可以利用它来隐藏并证明秘密，但该算法的能力有限，因为它只具备加法同态，也就是 f（a+b） = f（a） + f（b），但不具备乘法同态，即 f（a×b） = f（a） × f（b）。

这相当于把现实空间的物体投射到影子空间后，影子空间可以用加法来组合影子，但对于一些需要用乘法才能组合的影子，它就无能为力了。

怎么办？可以引入「配对函数」。比如椭圆曲线配对函数就是对椭圆曲线算法做一系列的调整，生成一个新的映射空间，这个新空间既满足加法同态，也满足类乘法同态（注意，只是类乘法同态），这样一来，除了用加法，我们还可以用类乘法去证明秘密。

现在，第二段旅程抵达了终点。我们需要了解的是，同态是证明秘密的关键所在，但并不是所有的映射关系都有「良好」的同态，而不同的应用场景对同态的要求也不一样，在实际的设计中，需要根据具体需求实现不同的同态。

如果原空间与映射空间既满足加法同态，也满足乘法同态，我们称其为全同态。全同态意味着可以对密文进行任意的运算（可以对影子进行任意方式的组合），这对实现数据隐私有着重要的意义，但实现全同态是一件非常困难的事情。

3. 通用零知识证明：NPC 问题

你一定注意到了，我们说椭圆曲线数字签名算法具有「零知属性」，却并没有说它是零知识证明协议，因为它的主业是做数字签名，隐藏私钥只不过是它必须要实现的一个功能。而且它也只能隐藏私钥，如果想让它帮你隐藏一个你自己的秘密，它是做不到的。

而零知识证明协议，比如我们熟悉的 zk-SNARKs，它的主业就是隐藏并能证明需要它隐藏的各类秘密。这是如何做到的？

让我们回到本文最开始的那个单向函数 k × P = Q，它能隐藏一个秘密 k，如果我们把它变复杂一些，比如变成 t × h = （v0 + a1 × v1 + …… + am × vm）（w0 + b1 × w1 + …… + bm × wm）这样一个多项式，是不是就有了很多可以隐藏秘密的「空间」，比如把秘密放在 a1，a2，……，am 中。

事实上，上文中这个复杂的多项式就是 zk-SNARKs 中用于实现零知识证明的多项式，该多项式能够证明各类秘密，因为它能证明布尔电路。

为什么能证明布尔电路，就能证明各类秘密？因为布尔电路可满足性是一个 NPC（NP-Complete）问题，而 NPC 问题有一个「特性」，即所有的 NP 问题（包含NPC）都可以在多项式时间内归约（转换）成某一个具体的 NPC 问题。

比如布尔电路、图论三染色、甚至我们熟悉的扫雷游戏，都是 NPC 问题。我们可以把扫雷游戏规约成布尔电路的可满足性，也就是能够用证明布尔电路的多项式实现对扫雷游戏的零知识证明；可以把图论三染色规约成布尔电路的可满足性，也就是能够用证明布尔电路的多项式实现对三染色的零知识证明……

因此理论上，我们能够以任何一个 NPC 问题为基础构建一个通用的零知识证明协议。但这仅仅是理论上的，因为使用它们做证明的难易度是截然不同的。目前主流的方法是选择布尔电路或算术电路，因为它们实现起来相对容易、电路规模小，zk-SNARKs 和 Bulletproofs 都是选择的这种方法。

4. 零知识证明协议

在三段旅程之后，零知识证明对我们而言也许不再是神秘莫测的事物，它背后有着简单逻辑：1. 单向功能是隐藏秘密的方法；2. 同态映射是证明秘密的基础；3. 证明 NPC 问题的多项式（但这并非唯一的方法）可以实现通用零知识证明。

不同的零知识证明协议在这三点上的具体实现是不一样的，最主要的不同可能体现在第 3 点中，哪怕证明的是同一个 NPC 问题，也可以有截然不同的方法。因为不同的设计，零知识证明协议最常被提及的差异主要包括：

1. 不同的计算空间和计算时间。更小的空间和更短的时间是我们不断改进零知识证明协议的主要动力，也是比较不同零知识证明协议的主要指标。

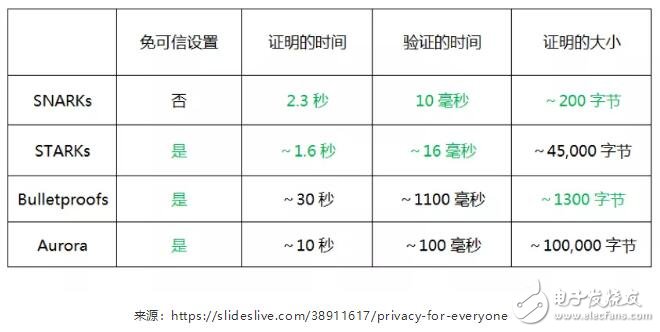
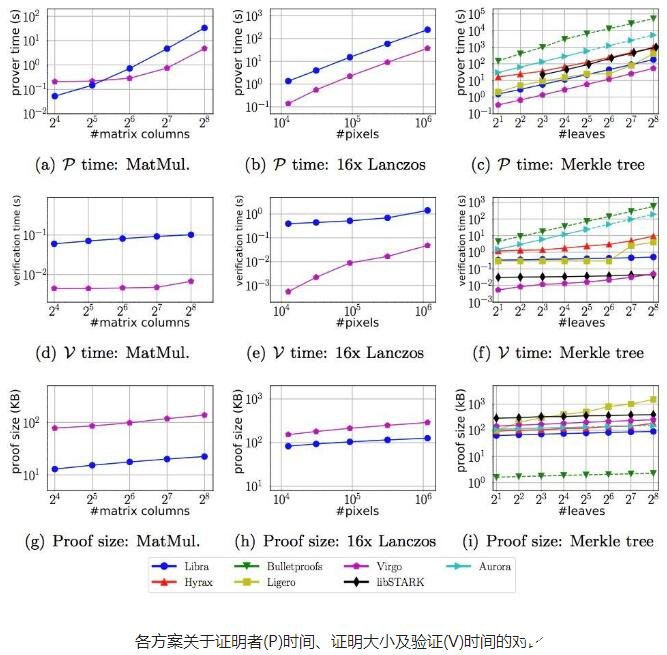
比如下图是 ZCash 首席执行官 Zooko Wilcox 在谈到零知识证明协议时用到的表格，主要比较的就是不同协议的证明时间、验证时间和证明大小。

2. 是否需要初始化可信设置。不需要可信设置当然更好，会减少信任问题和安全问题，不过新的证明方法就可能带来新的计算问题，比如 Bulletproofs 不需要可信设置，但它在高复杂度情况下的验证成本会很高。

3. 所依赖的安全假设。安全假设与安全密切相关，比如 Bulletproofs 依赖的是一个标准安全假设：离散对数问题，加上一个随机预言模型；而 zk-SNARKs 依赖的是一个不可否证的安全假设问题：指数知识假设。

上述的这些指标和属性很难被同时满足，因此在设计零知识证明协议，或者选择零知识证明协议/方法作为某个协议的功能组件的时候，需要考虑特定场景的需求问题。比如对证明时间有较高要求，就可能需要选择占用更多空间、或者具有较小通用性的方法；对可信设置有要求，就可能需要选择有更高证明成本的方法。

因此，一方面，零知识证明是不断发展的，各种不同的协议正在被设计出来，某些新协议在某些方面会更具优势；另一方面，不同的协议有不同的适用场景，要根据需求来做设计或选择，并没有一个适用于所有场景的更好的协议。

如果你愿意，旅程到此就可以结束了；如果你想继续，接下来的这一段有点「野」。

5. 另辟蹊径

这是关于 zk-STARKs 的。它也是零知识证明协议，但它是基于信息编码的零知识证明，这是完全不同的一条道路，并且有可能打乱你已经清晰的思路。

zk-STARKs 并没有使用密码学中的单向函数，简单理解的话，它是这样做的：假设 P 有 9 个要证明的数，a1，a2，……，a9，那么把它们编码成 b1，b2，……，b9，每个bi中都含有a1，a2，……，a9 的部分信息。在做验证的时候，验证者 V 对 b1，b2，……，b9 做抽样检查，从少量 bi 中就能分析出编码有没有错误，这样就可以大概率探测到 a1，a2，……，a9 是否属实。

当 V 对 P 作随机抽样时，P 能够主动用随机数混淆抽样的 bi，同时又能使 V 完成验证，从而实现零知识性。

所以 zk-STARKs 的「单向」并不是基于计算不可行的单向，它是因为没有暴露 b1，b2，……，b9 全部，导致无法通过 b1，b2，……，b9 反向计算出 a1，a2，……，a9。在「同态」部分，它也不是抽象代数（或密码学）中的同态概念，而是基于线性编码纠错理论进行抽样验证。

zk-STARKs 也不是基于上文介绍的 NPC 难题做验证，它是基于概率检查做验证的。关于这类验证方法，可以从一种古老的验证系统 PCP（Probabilistically Checkable Proofs）中找到线索，不过在 zk-STARKs 中使用的方法叫 IOP（Interactive Oracle Proofs），与 PCP 的不同之处在于它用的是 Oracle。

之所以介绍 zk-STARKs，一方面是因为它也颇为流行，另一方面是想说明零知识证明可能是一个难以探索到边界的事物，比如 zk-STARKs 就是迥异的，因此本文只是理解零知识证明的一个角度，且因为自身认知有限，这种角度也许并不适用于所有的零知识证明方法。
责任编辑；zl