EOS RAM在经过了价格大幅度波动后,其背后的Bancor定价机制也越来越为人所熟知。继《【火线视点8】没有免费的午餐——从EOS RAM价格看公链通证经济体系设计》后,火币区块链研究院继续对这一算法研究,分析其后背的数学和经济学原理,并通过公式,我们计算对比了不同参数下RAM价格,主要得到以下研究结果:
Bancor公式中隐藏价格函数与经济学上的价格弹性曲线的概念相通。
由于是根据供需量来得出价格,Bancor经过微积分计算得出购买RAM时所需EOS的等效价格,防止产生购买价格误差。
在不同的曲线参数下,价格会有不同。我们以北京时间7月10日18点40分的情况为例,使用MATLAB R2015a进行测算:付出10 EOS以上,参数取值改为0.5会比0.0005的商品“性价比”更高。
报告正文
1.引言
EOS RAM在经过了价格大幅度波动后,其背后的Bancor定价机制也越来越为人所熟知。继《【火线视点8】没有免费的午餐——从EOS RAM价格看公链通证经济体系设计》后,火币区块链研究院继续对这一算法研究,分析其后背的数学和经济学原理。通过公式,我们计算对比了不同参数下RAM价格,可看到参数的确会产生一定程度上的影响。
另外需要注意的是:测算得到的数据结果不是也不应被视为是对EOS RAM未来价格走势等情况的证明或确认。特此声明。
2.主要结论
经过研究与测试分析,我们得到以下主要结论及技术建议:
Bancor公式中隐藏价格函数与经济学上的价格弹性曲线的概念相通。
由于是根据供需量来得出价格,Bancor经过微积分计算得出购买RAM时所需EOS的等效价格,防止产生购买价格误差。
在不同的曲线参数下,价格会有不同。我们以北京时间7月10日18点40分的情况为例,使用MATLAB R2015a进行测算:付出10 EOS以上,参数取值改为0.5会比0.0005的商品“性价比”更高。
3.什么是Bancor
Bancor算法的本质我们在此前的《【火线视点8】没有免费的午餐——从EOS RAM价格看公链通证经济体系设计》报告中有过介绍:它是在1940年-1942年间由凯恩斯、舒马赫提出的一个超主权货币的概念,可作为一种账户单位用于国际贸易中,并由英国在二战后正式提出。然而,由于美国实力在二战后一枝独秀,Bancor 方案并没有在布雷顿森林会议上被采纳使用。但应用这一思想的 Bancor 算法则继续延续了其生命力。Bancor 算法由 Bancor Network 项目提出应用,旨在采用公式来设定好数字资产间的兑换价格。其联合创始人 Eyal Hertzog 近期也被BM邀请一起来探讨 EOS 中 Bancor 算法的应用。
虽然Bancor Network近期也经历被盗风波,但这不妨碍我们继续研究这一算法。既然是原本要用于国际贸易的模型,那必然涉及到不同实体间如何兑换。Bancor 白皮书中对定价模型有着十分严谨和详细的说明。它定义了两类token:一种是通常会流通使用的 connector token(即储备金,例如:BTC、ETH、EOS等),而另一种是作为“超平台”中间媒介的 Smart Token。为了使得兑换价格满足刚才提到的供需关系,设计的公式中的价格为 connector 的可流通余量(balance)除以 按照一定系数的Smart Token 供应量:

其中,CW 的英文是 Connector Weight,表示设计出来的 Smart Token 的总价值与实际在使用中的 connector 余量间的关系,设计好后为一个固定参数:

总体上来说,就是 Smart Token 的供应量越少或者 connector 的余量越多,那么使用 connector 来兑换 Smart Token 的价格就越高。
虽然很不严谨,但这也就能理解了为什么 EOS 的 RAM 越少,价格越高了。至于不严谨的原因,我们将在下文继续解释。
4.公式设计思路
回到 RAM 价格上,那么无疑在 EOS 主网刚上线的时候,RAM 供应量最多。可以看到最低价格是 0.017 EOS/KB 。按照这个价格,也就是买 1MB 需要 0.017 * 1024 = 17.408 EOS。那么,全部 64GB RAM 在这个时候值 1140850.688 EOS,是不是这个时候花费这些 EOS 就可以把 64 GB一次性都买下?答案显然是否定的。
实际上,有多种方式可以限制这种做法。最简单的一种就是限制每次买卖的数量:只要设置每次只能购买 32GB,那么第二次买 RAM 的价格就会提高很多,买的总成本就会变的很高。再循环细分下去为 16GB、8GB …… 总的价格就会越来越合理。这在数学上是有相应的工具可以使用的。
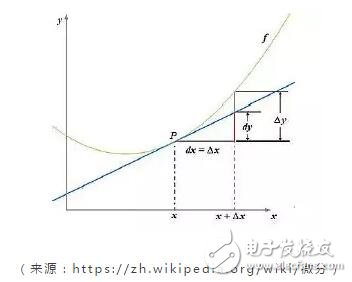
是的,就是微积分。在 Bancor Network 白皮书中引用的另外一个资料中,可以看到这个推导过程。
定义R为当前connector的余量、S为当前Smart Token的供应量、F为系数(即上文中的CW)、P为当前Smart Token的价格,那么有:
Smart Token的市场总量 = SP
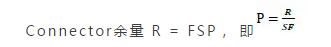
当要购买dS 的Smart Token时,用户需要付出P dS 的成本,也等于剩余connector的变化量,即dR = P dS
又因为R = FSP,同时微分可得到:dR = d(FSP) = F d(SP) = F(S dP + P dS),所以综合上述两个等式可得:

然后我们可以看到,这个微分方程的结果和经济学上的一个概念是一样的。
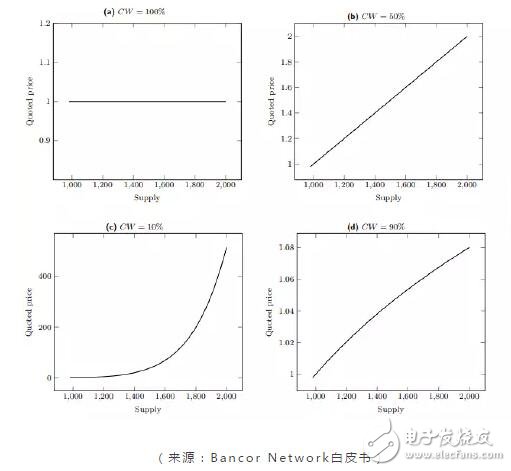
是的,就是经济学上的价格弹性曲线:
当 CW 或者 F 为 1 时,提供100%的流动性,因此价格毫无弹性,一直维持在某一水平线上
当 CW 大于 0 小于 1 时,即上述正常供需情况下的价格曲线
有了这个价格函数后,再对其进行积分,即可得到不同量的 connector 可换购的 Smart Token 数量。
定义用户要购买Smart Token的数量为T,那么可得到需要付出的connector的数量E为:

如果用付出的connector 除以兑换到的Smart Token 数量,即可得到等效价格(Effective Price),即只要付出的connector总量一样,不管分多少次购买,所获得的Smart Token总量是一样的,因此也就不需要限制单次购买量了。但相应的,如果单次付出不同数量的connector,折算得到的单价也会不一样,所以不会存在上文假设的“套利”情况。
5.EOS RAM的公式更复杂
EOS 应用 Bancor 算法过程中,并不是将 EOS 和 RAM 直接用价格曲线进行兑换,而是引入了中间 token——RAMCORE,对应于 Bancor 中的 Smart Token。
EOS 和 RAM 兑换逻辑的代码主要在:
https://github.com/EOSIO/eos/blob/v1.0.8/contracts/eosio.system/exchange_state.cpp
EOS 到 RAM 的兑换过程就涉及了两个公式,所以上文中用一个公式来举例就很不严谨,只是为了定性的说明价格特性。
从代码中可看到EOS与RAMCORE的兑换公式为:
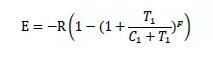
其中,E为EOS到RAMCORE所能兑换的数量,R是RAMCORE的初始发行总量,C1为当前EOS余量,T1为用于购买的EOS数量,F为常量参数
将上述公式的进行反向整理设计,即可得到RAMCORE与RAM的兑换公式为:
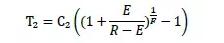
其中,T2是准备购入的RAM数量;C2为可分配的RAM余量。将中间变量E代入即可得出用于购买的EOS数量(T1)与可兑换到的RAM数量(T2)之间的关系。
为方便直观的理解,可以对公式进行简化,得到:

可以看到随着可买RAM余量(C2)的降低或者EOS数量(C1)的增多,RAM的价格会加速增长(即同样付出T1的EOS下,可换取到的RAM数量T2变少了)
6.不同参数下的价格偏差计算
根据简化公式,F 应该对价格影响很小。那么 BM 之前说的把 0.5 多除了1000,变成0.0005,对价格是否有很大影响?我们可以直接通过公式计算来验证。
按照公式,要计算先确定好公式中的参数。参数的获取可通过网络渠道来获得(参考https://github.com/eoshackathon/eos_dapp_development_cn/blob/master/docs/ram_price.md):

由于C1和C2的参数会时刻根据行情进行变化,我们选取上述时间作为示例计算参数。下一步,我们使用MATLAB(R2015a 8.5.0.197613)进行公式的计算。
当要付出不同量 EOS 时,分别计算出F=0.0005和F=0.5的 RAM 价格结果,可购买到的RAM之差(F=0.0005-F=0.5)以及两个价格之间的差值:

可以看到,当F取值变化的时候,不同购买量下的结果的确不同:当一次付出10000 EOS时,F=0.0005能购买到的RAM比F=0.5少了 20 KB,相应的RAM单价高了 4.0412e-04 EOS/KB;而当一次付出100000 EOS时,会少近 2MB,同时单价高 0.0040 EOS/KB。
根据结果,在购买量大的时候,确实会有区别,而且改为F=0.5后RAM的“性价比”反而会更高,这很可能也是BM及EOS社区在调整参数时所考虑的问题。
 电子发烧友App
电子发烧友App






















评论