我们为 V SYSTEMS 区块链平台设计了了一个注重高扩展性的权益证明(PoS)共识机制,称为超级节点权益证明共识(Supernode PoS)。该共识机制的特点包括固定的区块铸币间隔、冷铸币、以及权益流动性。
1. 能源的作用
早在 2011 年,比特币网络经历了可能是它的第一次显著增长。那时,绝大部分的比特币使用者及支持者们对于这一去中心化?网络的能源消耗问题可能并不关心。然而,Peercoin 项目已经提出了问题:能源消耗对达成共识真的必不可少吗?对于大多数比特币的鼓吹者而言,这个问题的答案是肯定的:比特币就像是黄金;挖金矿所消耗的能源给黄金赋予了价值,而比特币挖矿所消耗的能源不仅能使网络达成共识并保共识安全,也是比特币货币价值的支撑。
但回顾历史,人们对于是什么给予了黄金货币价值这一问题众说不一。奥地利学派推断其必然来自于某种初始的商品价值。有人推测,一旦民族国家有了足够的能力可以剥夺黄金的货币角色,那么黄金就应该没有什么价值了。只要人们相信比特币的货币效用,就自然会问道:到底是什么给予了比特币价值?
Peercoin 在一定意义上是在尝试解开这个最重要的货币奥秘。它成功地将工作量证明或(借用黄金挖矿而来的)挖矿的能源消耗从共识算法中分离了出来,并将能源的作用限制到仅用于数字货币的发行。接下来很容易考查能源仅剩的与货币发行的关联,因为人们可以切换到某种类似股票的发行模型,从而可轻易将能源成分从发行机制中剔除。
因而事实上,权益证明共识技术进一步表明了货币价值并非来源于能源消耗。而且,货币价值也不需要内在价值或任何其他类型的商品价值。仅由货币效用就可以赋予价值。
2. 权益证明共识—无能耗的共识
Peercoin 达成共识的方法极具开创性。它完全抛弃了比特币的取得惊人成功的工作量量证明共识机制,而去寻求一种完全不不依赖能源消耗的算法。它对权益证明充满信心,相信这一概念可以独立地形成一个共识算法,而不需要任何工作量量证明成分。
有的作者误解这一点。就共识算法而言, Peercoin 是纯权益证明的。工作量量证明仅仅用于数字货币的公平分配,并不不参与共识算法。
对于一个无能耗的共识系统,我们称产生区块的过程为铸币(minting),以区分于消耗大量量能源的挖矿过程。
Peercoin 的共识算法继承了了比特币的一些特征。例如,它也随机地产生区块,仅可以观察到平均区块间隔或目标区块间隔。与这一过程相关联的是一个称作权益证明难度的度量,对应于该度量量有一个?用于铸币的由共识协议维护的可调节阀值。
引入权益证明共识机制是区块链技术发展中的一个巨大里程。它不仅消除了为达到分布式共识?而进行挖矿的能源消耗,也极大增强了区块链的扩展能力,为区块链技术的各种应用铺平了道路。
3. 针对权益证明共识的批评
自从 Peercoin 开创性的面世后,常有人针对该系统某些方面提出批评。一个经常能听到的批评是“权益欺压(stake grinding)”。这种攻击在 2012 年Peercoin 最初版本发布后不久即被发现。Peercoin 于 2013 年2 月发布的 0.3 版本中实现了一个重要的新算法,以抵抗这种类型的攻击。
这个新算法引入了一个称为“核(kernel)”的共识字段。它是一个会随区块链逐渐变化共识数字:在给定的时间隔内协议会选中一个区块,被选中的区块可以改变核的一个比特位。核可以看成是区块链上的一个缓慢改变的随机源(entropy source),区块链的一个短分叉给它带来的影响将十分有限。有了核的保护,权益欺压的威胁就基本上被消除了。
另一个针对权益证明共识常见的批评为“无风险分叉(nothing-at-stake)”问题。该问题可表述为,由于铸币不涉及工作量或能源消耗,铸币者可尝试在区块树的所有分支上进行铸币而不会有任何损失。因而在利益的驱使下,铸币者将会在所有分支上进行铸币,以避免某一给定分叉输掉竞争而导致的损失。这种论证的问题在于它忽略了权益证明的核心原则。权益证明的思想是,当某人在货币供应中拥有了的一定比例的权益后,他应当已有激励去做对整个系统有益的事情,而不会对系统进行攻击。由于在所有分支上进行铸币可认为是对协议的一种攻击,它已经是权益证明所不允许的了。按这样的观点,即便是所谓的理性铸币者也不应当以内部货币单位来估量价值,而应当以外部稳定货币来衡量其权益的总价值。
考虑到对权益价值可能的负面影响,这或许与公地的悲剧有一定关联。然而,即便按公地悲剧最初的解释,可能避免的少量铸币损失也比不上权益价值潜在损失的量级。事实上,没有证据表明“无风险分叉”导致了任何为进一步制止该攻击而作出的协议调整。
4. 关于冷铸币的争论
在权益证明共识面世后不久,Peercoin 社区就掀起了了关于冷铸币(cold minting)特征的讨论。它与比特币称为冷存储的特征有关,即私钥由离线钱包进行管理理。由于权益证明共识要求铸币者对区块进行签名,为此其私钥必须保持在线。这与冷存储可获得的高安全性是矛盾的。
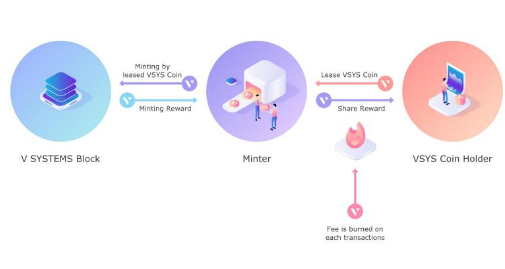
解决的办法是将铸币与消费的角色相分离。也就是说,权益所有权的密钥与铸币所需的密钥可以是不同的。那么,铸币密钥保持在线的同时,所有权密钥可以放置在离线存储中。这自然就会允许出现铸币池(minting pool),类似于比特币的矿池。鉴于比特币矿池的中心化倾向,铸币池也是不被赞成。
考虑到众多因素,冷铸币特征并未在 Peercoin 中实现。而在其他一些权益证明系统中确已经实现了铸币密钥与所有权密钥的分离。这种分离现在通常被称为权益代理或出租。
5. 向超级节点的转换
区块链行业在最近几年年中见证了去中心化应用的巨幅增长。比特币与以太坊都出现过周期性交易拥堵。越来越多的关注点投向了单一区块链的表现上。
这就已经为共识算法的设计带来了几个问题。首先,挖矿或铸币节点可能没有足够的激励升级节点硬件。且这种节点也可能大量存在。由于整个网络的维护成本非常之大,有的节点在硬件升级上注定会被甩在后面。
另一个问题与比特币产生区块的随机过程有关。尽管平均区块间隔是 10 分钟,但有时候下一个区块的产生需要等待比这长得多的时间。对于面向性能的系统而言,这就成了一个问题。这类系统更倾向于固定的而非随机分布的响应时间。
如上的考虑,铸币协议应当设计成有固定的区块间隔,且要将铸币节点提升到比网络中其他节点更重要的位置。
6. 铸币时段与铸币权竞争
为实现铸币的固定区块间隔,我们定义一个称为铸币时段(minting slot)的实体。每个时段对应于铸币权的一次平均分配。因此,为获得某个时段的铸币权,一个潜在的铸币参与者必须取得该时段的所有权。
在每分钟内定义了60 个铸币时段,每个时段对应于其中特定的一秒钟。要在给定的一秒钟内取得铸币权,必须取得该秒对应铸币时段的所有权。
基本上系统中的铸币者将会轮流着进行铸币。这样做的好处是,如果有某些超级节点停?止了铸币,不管出于什么原因,他们对系统响应及吞吐量的影响都会被最小化。
每个超级节点的本地时钟都通过网络时间协议进行同步,以保证铸币活动的正常顺序。回到 2009 年年,比特币选择不依赖于网络时间协议进行时钟同步,所以比特币协议允许矿工们时钟偏移多达 2 个小时。通常而言,现今的网络时间协议可以作为一项基本的互联网服务,与域名服务类似,因而可以合理地假设其有很高的安全性。
铸币时段的竞争可以允许在任意时间自由进行。挑战者可以选择一个时段向当前的铸币者发起挑战。为防止滥用挑战,挑战者需要支付一笔较高的挑战费。当挑战者发布一个竞争交易后,协议将检查竞争者与当前铸币者的质押权益以决定谁是竞争的胜出者。
7. 铸币经济
铸币者参与铸币的质押权益包括其拥有的且未租借给别人的数字货币,以及其他用户租借给该铸币者的数字货币。术语“租借(lease)”指明的关系为铸币者通常以铸币池形式运行,并需要给数字货币的拥有者支付一定利利息。在租借期间,货币的所有权并未转让,因此铸币者不能花费或转让租借来的货币。
铸币时段的平等铸币权使得网络中超级节点拥有平等的地位及相同的铸币输出。这与比特币挖矿设计形成鲜明对比。在比特币挖矿中,没有内在机制防止矿池市场形成垄断,其已成为了系统去中心化目标的一个现实威胁。
铸币时段的平等铸币权在铸币经济中扮演了了一个不可或缺的角色。超级节点形成了一个由铸币池组成的市场。铸币池市场决定租借的利率。由于权益所有者有将权益租借给支付更高利率的超级节点的理性偏好,而对于支付高利率的超级节点来说,铸币输出(即收入)是固定的,租借来更多的权益将会迫使它降低租借利率,所以存在一个平衡点,其作为一种内在的力量迫使超级节点的租借利率趋于相等。
V SYSTEMS 平台也采用了Peercoin 的手续费销毁模型以降低通胀率,同时消除铸币者之间的利益摩擦。
对超级节点硬件资源的要求将通过共识协议范畴之外的社区力量进行标准化与提升。
8. 权益流动性与频繁竞争攻击
以往的权益证明共识系统对于权益在参与铸币后的移动行为进行了诸多限制。尽管在技术层面这可能有其合理考虑,但在经济层面,它却是用户参与铸币的一个进入门槛。
然而,在权益证明共识中,参与铸币的权益数量直接关系到共识的安全等级。从这个意义上讲,对权益的移动不加任何限制是对网络安全有益的。称不限制权益移动的这种性质为权益流动性(stake liquidity)。有了权益流动性,铸币者可以随时花费或转让其拥有的权益。而租借权益的人也可以随时解除租借关系,并花费或转让其权益。
权益流动性也引入了某些攻击的可能性。从权益证明的角度来看,不应当允许使用同一权益在多个铸币时段索取铸币权。然而由于权益具有流动性,或许可以利用这种流动性尝试快速移动权益, 为权益获取比其应得的更多的铸币时段。称这种类型的攻击为频繁竞争攻击(busy contention attack)。
抵抗这类攻击的办法是为账户余额引入某种度量,其类似于铸币时段竞争的累加平均。思路是,权益必须留存在账户中一段时间,以等待账户度量恢复到满额,这样即可阻止频繁竞争攻击。
9. 账户模型与余额
传统的记账系统使用账户模型,它密切监测一个称为余额的可变状态以及相应交易历史。比特币内部使用了一种不同的形式,我们称之为币袋(coinbag)模型。想要获得账户余额,则需要收集与账户或地址相关联的币袋信息,并将各个币袋的货币数目相加得到余额。过去几年,许多加密货币系统都用回了更传统的账户模型。V SYSTEMS 也采用了账户模型,使得能更有效监测余额。
定义了租借关系之后,每个账户的基本余额可以描述为两个不同的部分:一是标准余额(regular balance),即用户拥有的余额;另一个是铸币余额(minting balance),它是标准余额加上租借来的余额并减去租借出去的部分。这两种不同的余额会随着相关交易易的确认而即时变动。
10. 关于余额模式的提议
10.1 币龄
币龄(coin age)被定义货币数量与持币周期之积。例如,以币天(coin-day)为单位的币龄就是货币数量与持有这些货币的天数的乘积。
仍使用 Peercoin 白皮书中的例子,如果 Bob 从 Alice 那里收到 10 个币并持有这些币 90天,那么我们就称 Bob 累积的币龄为 900 币天。另外,当 Bob 花掉了从 Alice 那里接收到的 10 个币时,就称 Bob 用这 10 个币累积的币龄已经被消费(或销毁)了。
作为控制铸币概率的价值证明,币龄显示出了它的优点与稳定性。然而,由于它是一个基于交易的量,计算复杂度与给定时间内所执行的交易数量有关。而且,币龄也并不是一个能体现出铸币者对社区贡献量大小的准确值。
10.2 已确认余额
已确认余额(confirmed balance)指的是经 N 个区块确认之后的铸币余额(总的标准余额 + 租入 -租出)。
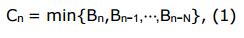
其中,Bi 是在?高度为 i 的区块中的铸币余额。N 是一个用来估计作?用区间的常数。已确认余额的优点包括:
· 余额不不会因某些大额输入而立即增加,但会因大额转出而立即减少;
· 为了得到一个很?高的已确认余额,矿工/铸币者需要收集并长时间持有货币。
然而,已确认余额本身也有缺点:
· 在一段时间内连续或累积的输入不不影响这段时间内的余额计算;
· 计算复杂度为 O(N )。对于高速铸币情形,为了了达到较好的性能与较高的稳定性,需要选取一个较大的 N。此时,O(N ) 算法将会是对系统性能造成影响的一个因素。
10.3 关于余额计算方式的提议
10.3.1 加权平均余额
为克服已确认余额的缺点,并降低计算复杂度,我们需要为高速挖矿/铸币的区块链系统设计一个新的、有更多性质且更容易计算的余额模式。
借鉴操作系统平均负载以及随机过程公式的思想,我们设计了如下加权平均余额:

这一新余额模式的计算复杂度降到了O(1) ,只需在每次铸币余额发生变动时记录一下加权平均余额。而且该模式下余额的最快增长速度是线性的(参看例11.1)。但是,从例11.1.1 及例 11.1.2 可以看出,如果余额频繁变动,则加权平均余额的下降速度会变慢。此外,这也是一个好的性质,只要总的加权平均余额受控的话。受控意味着余额不会莫名其妙地被创造出来(类似于物理学中的能量守恒律)。从例11.2.1 及例11.2.2 可以得出加权平均余额公式并不满足守恒律。
10.3.2 铸币平均余额
为使加权平均余额拥有好的性质,并克服其缺点,我们提出一个新的余额模式,称为铸币平均余额(MAB),其定义如下:
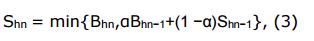
其中,Bhn 表示高度在 hn 时的当前余额。
铸币平均余额是取当前余额与加权平均余额的较小者。计算复杂度仍为 O(1) 。而且,在这个公式中,如果用户将其所有余额转出,则 MAB 会直接减为 0。有了了这个性质,总的铸币平均余额将会是守恒的,且被总余额所控制。
11. 一些例子
本章中,我们将设计许多数值实例例以展示铸币平均余额的性质。假设铸币的速度为每秒一个区块,则一天中可以得到 24 ×60 ×60 = 86400 个区块。本章中,我们对所有例子都取 N = 86400。而且作为理想情形,我们也令所有交易手续费为 0。
11.1 增长与下降速率
本章的第一个例例子是关于余额增长与下降速率的。
11.1.1 简化的增长与下降速率
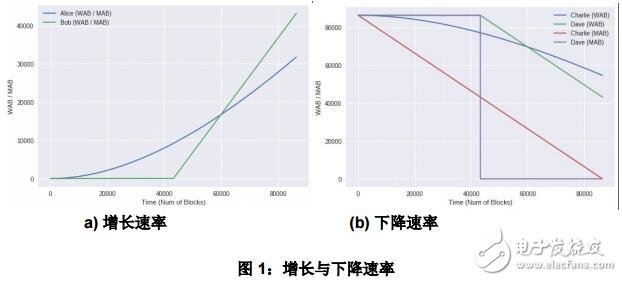
设 Alice 与 Bob 的初始余额都为 0。Alice 在每个区块产生时都能得到 1 个币,而 Bob 在高度为 43200 的区块上可一次性获得 86400 个币。Alice 的增长表现可用几何级数公式计算。图 1a 展示了一天内 Alice 与 Bob 的加权平均余额以及铸币平均余额的表现。
类似地,设 Charlie 与 Dave 的初始余额/WAB/MAB 都为 86400。Charlie 每个区块都减少 1 个币,而 Dave 在高度为 43200 的区块中失去 86400 个币。图 1b 展示了了一天内Charlie 与 Dave 的加权平均余额以及铸币平均余额的表现。
11.1.2 缓慢下降速率
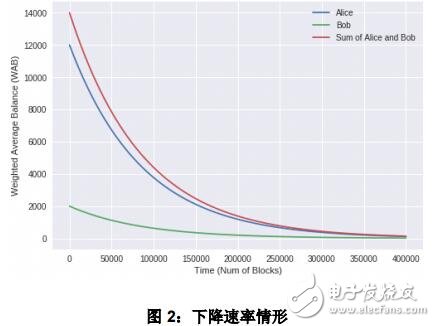
设 Alice 和 Bob 分别有初始加权平均余额 12000 和 2000。设初始区块高度为奇数,仅Bob 有余额 1,且 Bob 在区块高度为奇数里将他所有余额转给 Alice。类似地,在区块高度为偶数时, Alice 将其所有余额转给 Bob。图 2 展示了400000 个区块内 Alice 与 Bob的加权平均余额情况。可以看到两者 WAB 之和在缓慢下降。而如果 Alice 与 Bob 在这段时间内没做任何动作,那么他们 WAB 之和应当在高度为 86400 时等于 1。
11.2 余额守恒律律
我们将给出几个例子来说明铸币平均余额(MAB)的良好性质。
11.2.1 守恒律律
在这个例子中,Alice 与 Charlie 的初始 WAB 以及余额均为 100,而 Bob 与 Dave 的初始WAB 与余额均为 0。在高度 h =0 时,Charlie 向 Dave 转了100 个币。在另一个组中,Alice 与 Bob 将每隔 10800 个区块交换一下他们的余额。图 3 表明每个组中的总余额是守恒的。
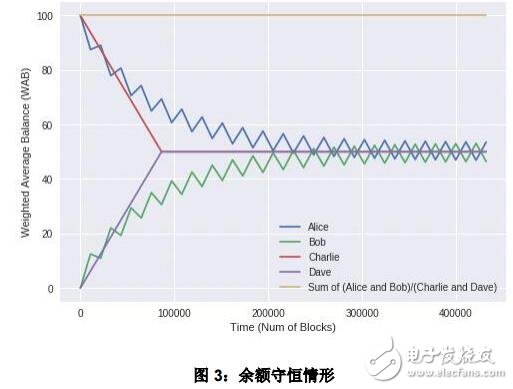
11.2.2 非守恒情形
在这个例子中,Alice 的初始 WAB/MAB 以及余额均为 100,而 Bob 与 Charlie 的初始 WAB/ MAB 以及余额均为 0。在高度 h =0 时,Alice 向 Charlie 转出 80 个币。而后,Alice 与 Bob 每隔 10800 个区块交换一下余额。图 4a 与 4b 显示了了两个余额计算公式之间的差异。
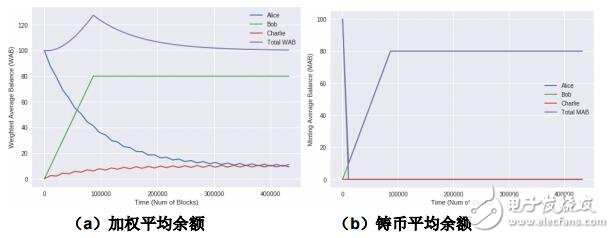
从图 4a 可以看出总的 WAB 在某些区间内会超过 100,即意味着利用某些“好”的策略略可以创造更多的 WAB。然而,图 4b 表明总的 MAB 总是小于 100,而这在实际应用中是一个好的性质。
11.3 铸币者的铸币平均余额
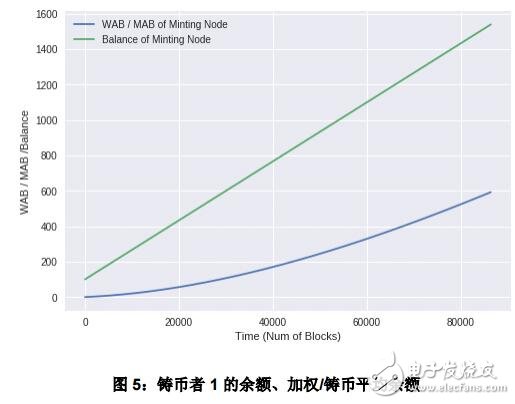
在本例例中,我们将展示一些关于铸币者的情况。第一个铸币者的初始余额 100,而初始WAB/ MAB 均为 0。铸币奖励为每分钟 1 个币。
图 5 展示了了一天内 WAB、MAB 以及余额的变化情况。
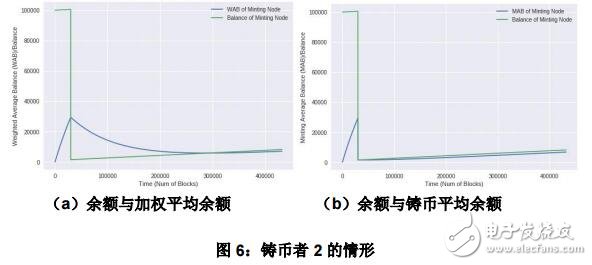
第二个铸币者的初始余额为 10000,初始 WAB/MAB 为 0。铸币奖励仍为每分钟 1 个币。在高度为 500 时,铸币者将其余额内的 99000 个币转出。
图 6a 及 6b 展示了了在五天内 WAB、MAB 以及余额的变化情况。
12. 总结
超级节点权益证明共识(SPoS)是朝着高性能区块链系统的一个演化过程。生态资源可以更更有效地向超级节点的硬件升级倾斜,系统响应不不仅更更快?而且更更加可预测、更更加稳定。我们也设计了了铸币平均余额以?支持权益流动性。
 电子发烧友App
电子发烧友App























评论