为了了解tangle是什么东西,我们得先了解什么叫有向图。
有向图是点(下图中有数字的方格)还有边(下图箭头线)的集合

其中Tangle是IOTA的资料结构(像以太和比特币都是区块链的资料结构),Tangle是一种特殊的有向图。Tangle上面保存了交易。每笔交易由一个点代表(vertex)。当一个新的交易要加入Tangle。他必须验证之前Tangle上的两个交易,每个验证会增加一个边(edge),所以加入一笔交易,会在Tangle上增加两个边。
用同样一个例子来解说
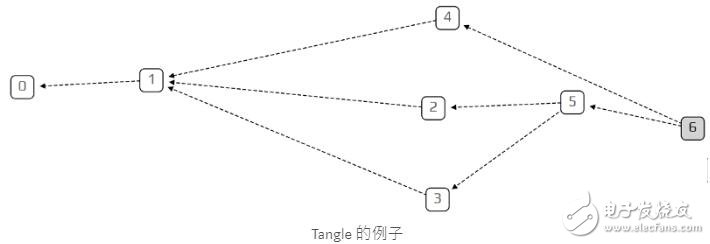
像在上面的Tangle中,交易5验证了交易2交易3,然后交易5又被交易6验证。在这篇文章暂时还不会讨论验证的详细过程,目前只要当作验证是确认上一笔交易有没有花超过该帐户余额就好了。
我们称呼还没被验证的交易叫做tips(毕竟他会在整个Tangle末端的地方)。像上图交易6就是一个tip。每一个新产生的交易都需要验证两笔tips的交易(至少至少至少要一个)。选择需要被验证的tips的演算法是IOTA技术的特色。
但为了循序渐进,我们会从最简单的方法开始: 我们随机抽取任意两个tips,并且每个tip 被抽到的机率都是相等的。
为了展示tangle在这种随机抽取策略(讲得比较专业一点叫“uniform random tip selection”)下tangle会长什么样子,IOTA Foundation做了动画模拟展示。这个模拟随机产生了一个tangle,这个随机的tangle会由一个创世区块(genesis)开始。在这个展示中,最左边是创世区块,最右边是最新的交易(tips)。tips会以灰色表示。当滑鼠滑到任何一笔交易上面的时候,被当下交易验证的交易会以红色表示,验证当下交易的交易会以蓝色表示。
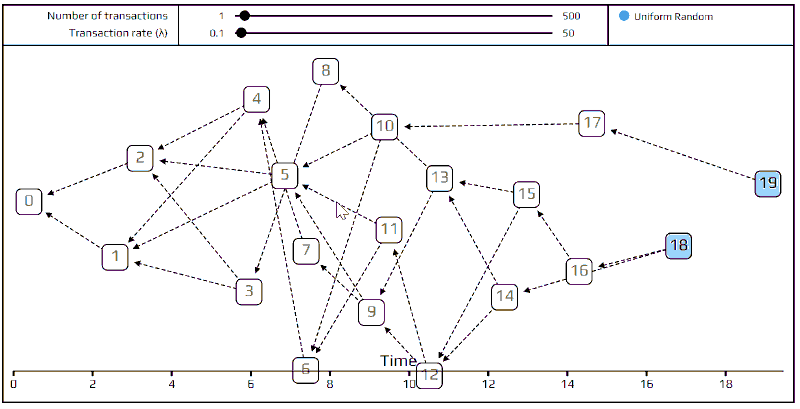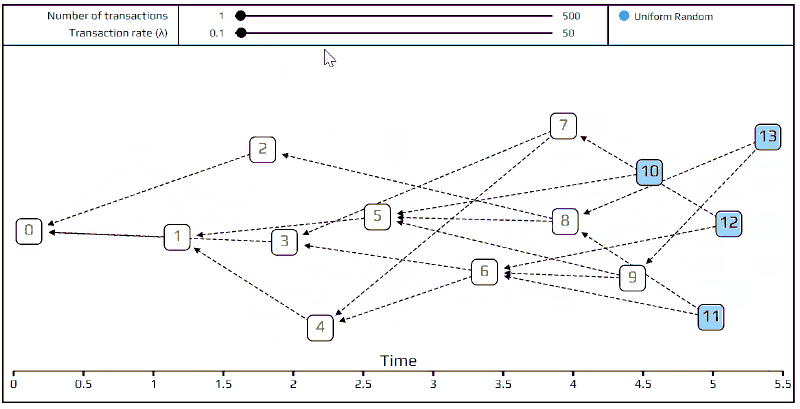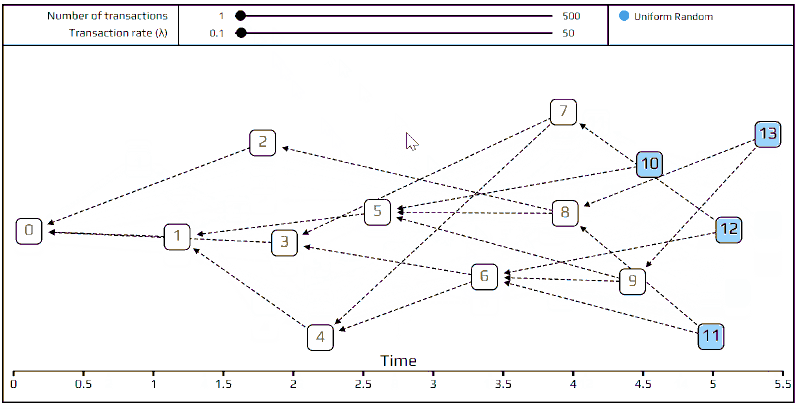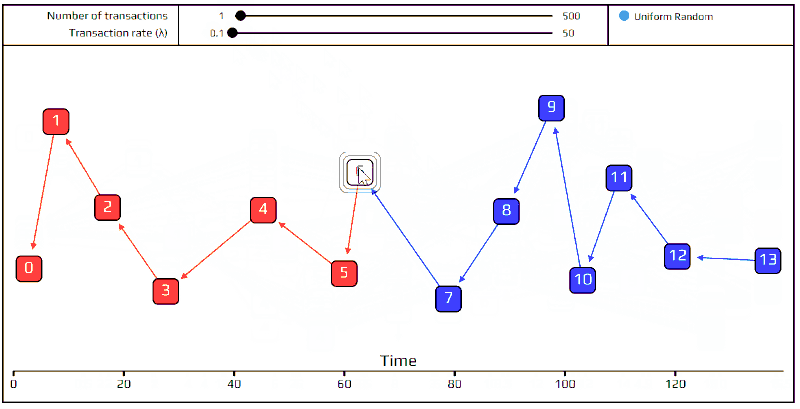
在上面的模拟中,你或许已经注意到交易并不平均分散在各个时间,而是在某些时间会特别的「繁忙」。这个让模型更加真实的随机方式,是使用帕松过程去模拟交易抵达而完成的。而这个模型在分析多少客户在指定的时间段之中走进商店,或者多少电话打进客服中心的这些例子中非常普遍。我们可以于下图中看到这个行为如何用在纠缠。交易4、5、以及6几乎同时抵达,而交易6之后有个长的中断,暂时没有新的交易发出来。
对我们的目标来说,我们只需要知道一件关于帕松分布事情:平均而言,进入的交易速度被设定为我们称为λ的常数。例如,我们设定λ=2,交易量为100,则总模拟时间将会是50次每单位时间。试试看吧!
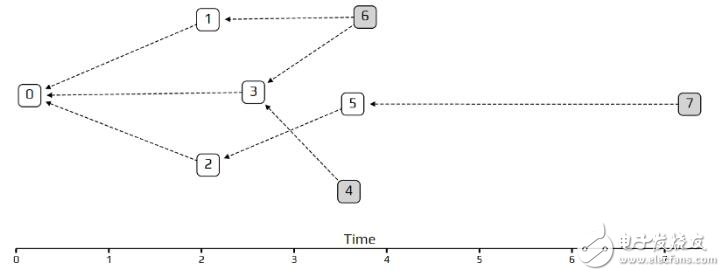
在开始之前,一件需要说明而更有趣的事情是;如果我们设定λ为非常小的数(例如0.1),则我们就可以得到「链」。一个交易不是认可(approve)两个,而是只认可(approve)前一个交易长得像链的缠结,这是因为交易将变慢以至于任何给定的时间内,只有一个端点(tip )去认证。在另个极端状况中,如果λ很大,所有的交易将抵达得很快,使得它们所见到的唯一的端点即是创始端点(创始交易所产生的端点)。这就是模拟的限制:以一个很大的λ和固定的交易量,我们将在相当短的时间段中进行模拟。
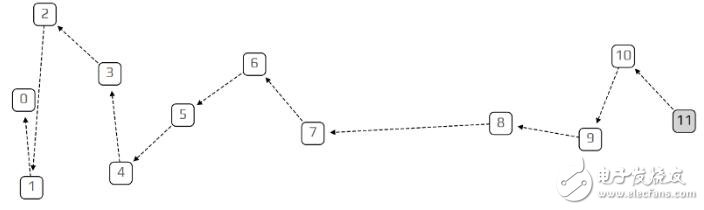
非常小的 λ所生产的链
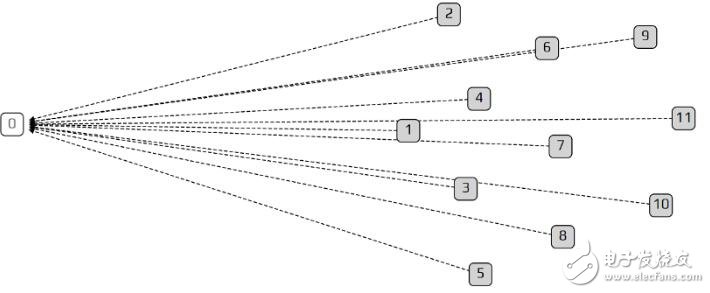
非常大的λ:只有创始端点是可见的
所以什么是交易看不「见」前一个端点呢?在模型中,我们让每个交易它抵达后一定时段内是不可见的(invisible)。我们使用字母h标示延迟的时间长度。这个延迟表示该交易被准备以及透过网路传播的时间。在我们的模拟中,我们常常设定h=1。这代表我们只能在过去的每段单位时间内,认可最少一次的交易。这个延迟不只是很务实的小细节,也是缠结最基本的性质,如果没有这个延迟的话,我们将得一个非常无聊的链。这个延迟是真实世界中,各个节点广播通知彼此有新的交易出现所花费的时间。加上这个参数,也使得我们的纠缠和现实世界的状况更加接近。
最后,来讲更先进的节点选择演算法─「无权重随机漫步」。使用这个算法,我们在创始交易(genesis transaction)上放一个「随机漫步者(walker)」,然后让该随机漫步者开始「走向」端点。每一步,它都跳往一个我们最近直接认可(directly approve)的交易。因为我们在选择要移动去哪个交易时,移动到每个交易的机率是相同的,这就是「无权重」一词的由来。下面我们做了一个模拟来表示它如何进行。
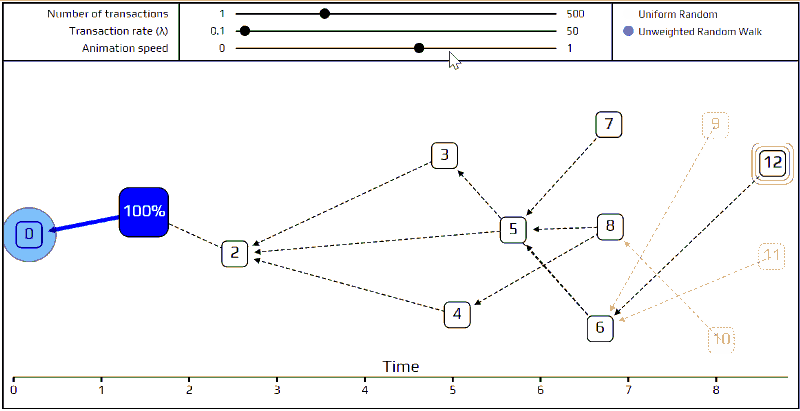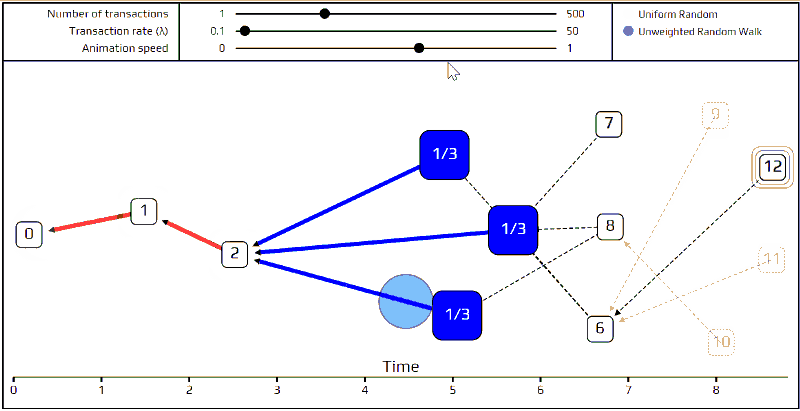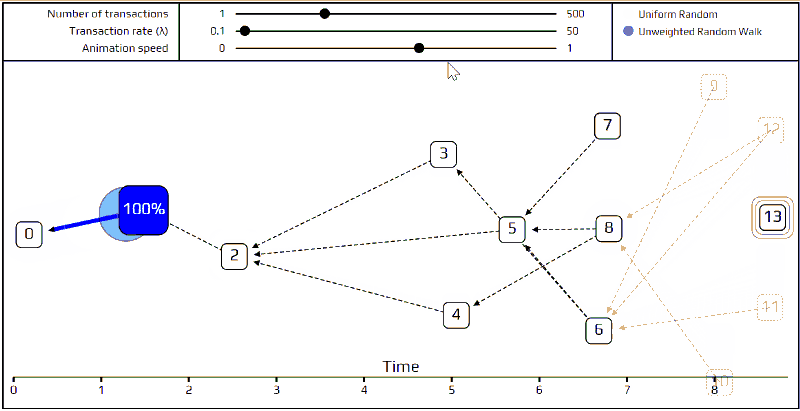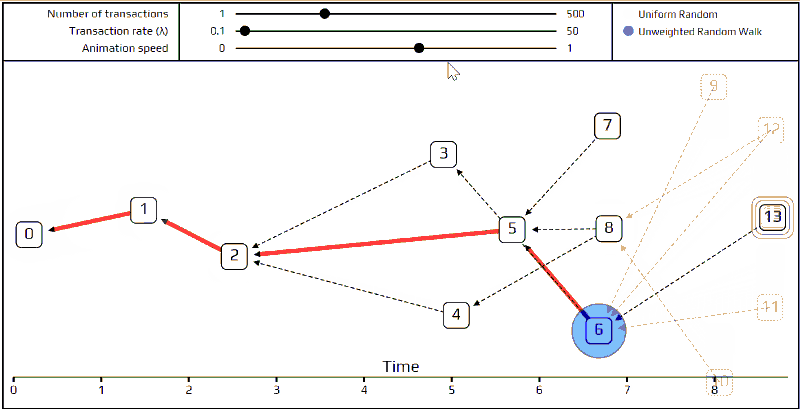
你们可以看到这个随机漫步者所移动的路径被标记为红色,每个有着不同的可能路径的连接点则被标记为蓝色。对于那些刚发布的交易们,因为太新了,对于随机漫步是「不可见」的,这些不可见的交易则被标记为透明的。
在学会无加权随机漫步( unweighted random walk)后,接下来要介绍他的进阶进化版加权随机漫步( weighted random walk)。
为什么要舍去无加权随机漫步转而使用加权随机漫步呢? 因为我们必须避免懒惰端点(lazy tips)的存在。所谓懒惰端点是指这个端点(tips)完全不跟上tangle的最新状态,在广播(broadcast)自己的每一笔交易的时候只认可之前旧的交易。这样的懒惰端点对于整个IOTA网路没有任何帮助,新的端点永远不会被认可到,整个IOTA网路会停滞不前。
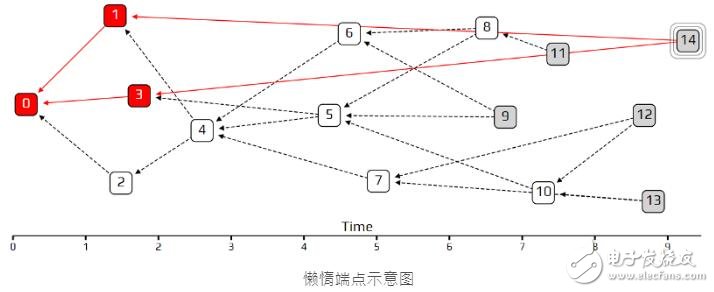
在上面例子中,交易14就是一个懒惰端点,因为他认可的交易是非常久之前的交易1 和交易3 ,如果我们使用均等机率的随机漫步,这样的懒惰端点交易14 被认可到的机率跟其他一般的端点是一样的,这样就很大的程度的鼓励了这种对于社群有害的行为。
要如何解决这种问题呢? 如果我们强迫所有的人只能认可最新的交易,这样的行为就跟去中心化的想法背道而驰。每个使用者、每笔交易都可以认可任何一笔他们想要的交易。我们没有可信的办法可以判断交易时间上的先后顺序,所以要去实践认可最新交易的这个方法,是有困难的。我们的解决方法是开发出一个内建的共识机制去避免这种状况的发生,因此可以让懒惰端点比较不可能被其他人认可到。
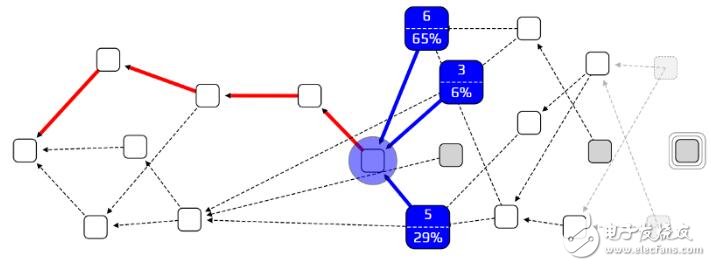
我们的解决办法是要给随机漫步一个偏置量(bias),借此让我们比较难选到懒惰端点。我们用累积加权(cumulative weight)去表达一个交易的重要性。我们更容易走到(选到)一个加权值较大的交易而不是一个加权值较小的交易。累积加权的计算方法很简单,就是
去计算这笔交易有多少交易给它直接或间接认可,再+1
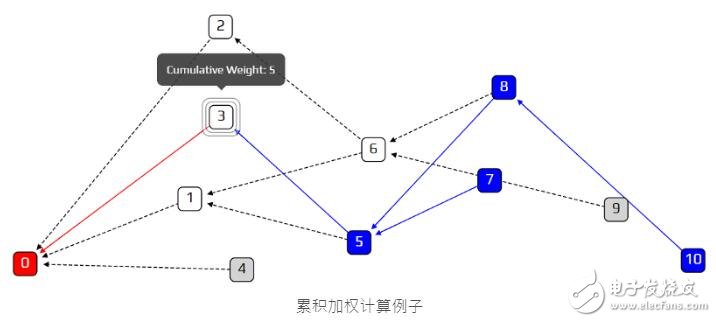
以上图为例,交易3 因为被交易5 直接认可,交易7、交易8、交易10 间接认可。因此这样得到
· 累积加权值= 1(直接认可数) + 3(间接认可数) + 1(公式要求加的1)
为了要展示一下累积加权的效果,我们再透过另外一个懒惰端点的例子来进行说明。
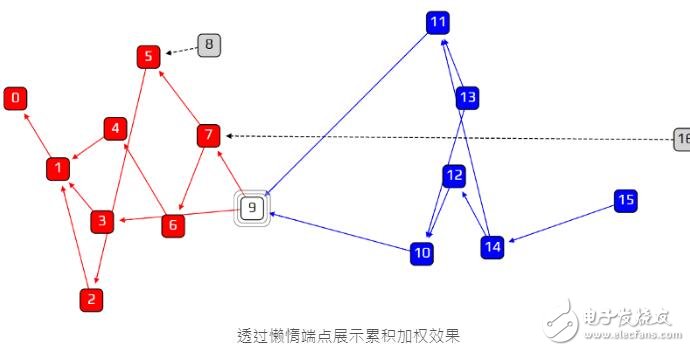
在上图,交易16 是一个懒惰端点。为了要选到交易16,我们的随机漫步必须先到交易7 并且跳过交易9,才能选到交易16。然而这种状况不太会发生,因为交易16 的累积加权只有1,然后交易9 的累积加权有7,相比之下交易9 的累积加权大得多。因此累积加权是一个有效遏止懒惰端点的方法。
但这样可能会有另外一个疑惑冒出来: “我们真的需要这些随机性吗? ”如果用一个超级加权的随机漫步( super-weighted random walk )呢?透过这种方法,我们的随机漫步在要选下一笔交易的分岔点时,可以永远只选加权值最大的交易就好,不需要任何的随机性及机率“,我们会得到的tangle会变成下面的图示一样。
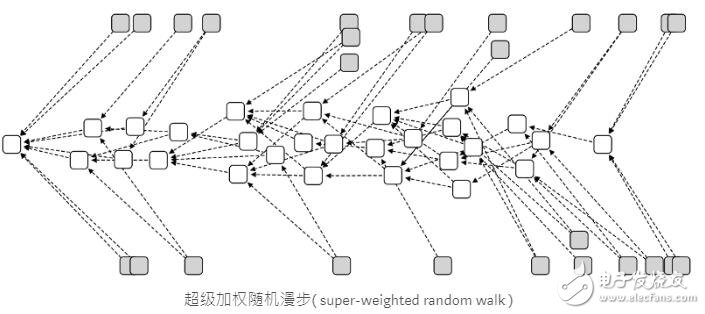
在这个tangle 中,灰色方块是没有任何人认可过的tips,一个正常的tangle 应该是希望每个tips 在右边(时间比较后面)的地方有其他tips。但像这样散落后面没有接tips 就会有点问题。这些散落的tips 没有任何交易去给他们做认可。这就是我们如果对随机漫步给予偏置量太多时会产生的问题: ”如果我们坚持只选择累积加权值最大的交易,这样就会有很大比例的交易永远不会被认可到“,这样也就会产生像上图一样,中间是被认可成功的交易大道,两旁散落着一些被遗弃的交易。
因此我们需要一个方法去明确定义,在分岔点时,选每个不同交易认可者的机率。这个过程使用的确切公式不是说十分重要,只要我们给予加权值比较大的交易一个偏置量,并且透过一些参数去控制这个偏置量多大这样就好了。因此在此我们在这边接绍一个新的参数α,α控制交易累积加权值的重要性。α的明确定义在白皮书里面有,如果有需要以后也会有专文件绍。
如果α=0这样就会回归无权重的随机漫步。如果α非常大,这样就会变成超级加权随机漫步( super-weighted random walk )。所以在这两极之间,可以找到一个平衡,这个平衡点可以充分的处罚懒惰端点,而且也不会造成太多的tips被遗落在外没有被认可。如何找到这个理想的平衡点是一个IOTA很重要的研究项目。
决定每一步随机漫步选取机率的方法叫做马可夫链地卡罗 (Markov chain Monte Carlo)简称MCMC。马可夫链的特性是每一个状态的分布概率都跟之前的前一个状态有关,之前的其他状态都没有关系(独立的)。
如果有任何新点子都可以透过模拟去展示,我们很建议读者在读完之后玩玩不同α和λ ,可以看看不同的值下会产生怎样不同的tangle。
到目前为止,我们已经介绍过有向无环图(DAG)、随机漫步(random walk)、和各种不同交易端点的选择法(tip selection mechanism)。在本篇文章,我们终于要来谈谈有关钱的事情。这次,我们要来介绍什么叫做”交易A 认可了交易B“。
就像本系列前面谈到的,每一笔交易都包含着交易资讯像是”Alice给Bob 10 IOTAs“。交易认可者的工作第一步就是确认是不是Alice真的有10 IOTAs可以给Bob。
可能有些人会疑惑那这些IOTAs从哪里来的呢? (好啦其实我觉得大家没有疑惑) IOTA跟其他知名的币像是以太币还有比特币不同的地方是,IOTA不需要挖矿, IOTA在创世交易( genesis transaction )时就产生出了所有的IOTAs,从此之后不会有任何新的IOTA被产生,IOTA的数量也就维持定值。在创世交易时,就将IOTAs传给一开始的投资者(ICO投资者)。在这之后,这些使用者互相交易,就构成了现在的交易网路。
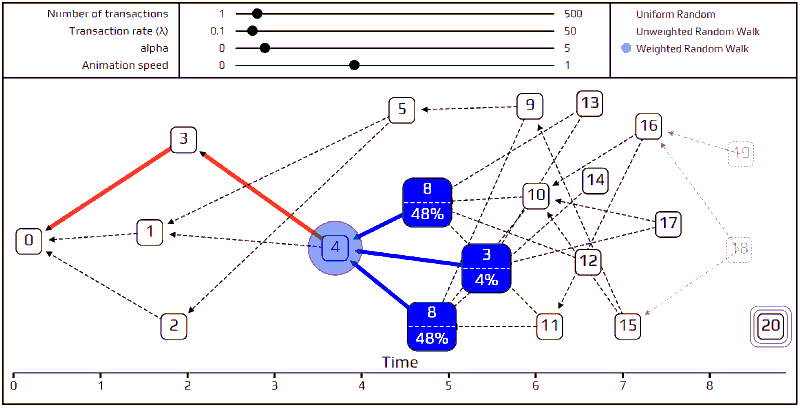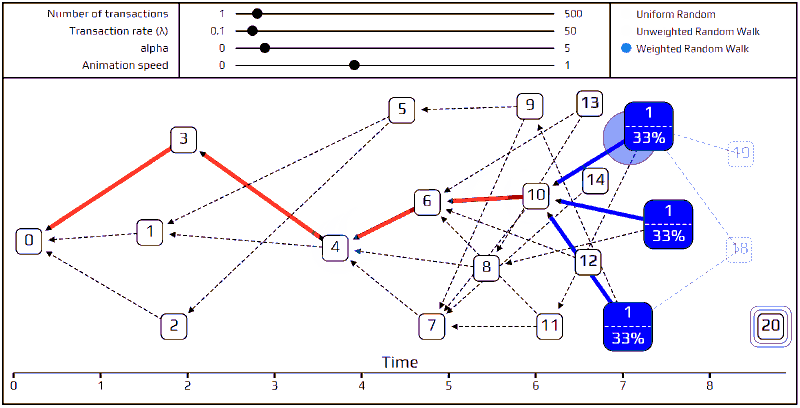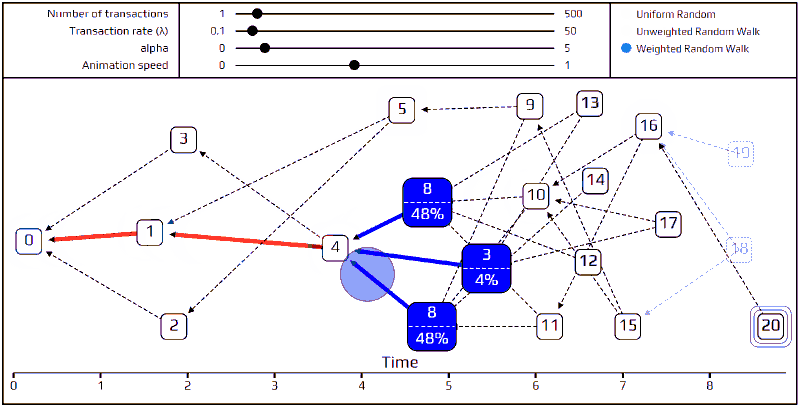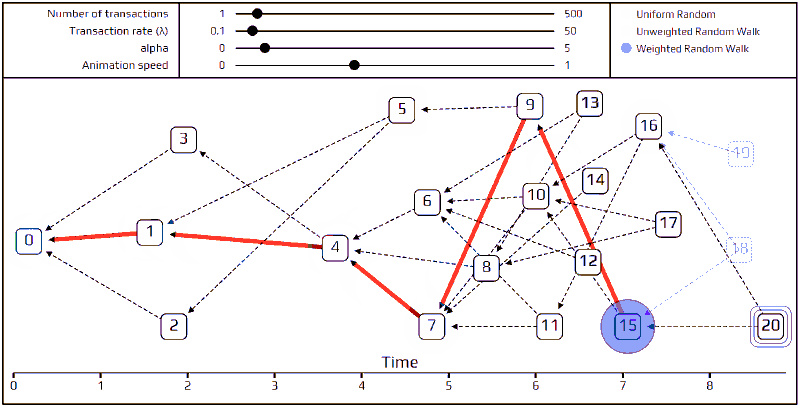
好的让我们回过来看看Alice 和Bob,用他们来做个很简单的范例。下面的小框框代表了一个交易,为了方便起见,我们把他们两个人交易前和交易后的帐户余额都写上来。我们可以看到,在一开始Alice 有10i,在给了Bob 10i后Alice 什么都没有了。

过了一阵子,有一个人叫Charlie,他自己做了另一笔交易。在他跑了端点选择的演算法(tip selection algorithm)后,判断他需要认可Alice 的交易才行。为了完成认可,他需要确认Alice 真的有10i 可以供花费。而且Charlie 如果没有认真验证的话对自己也没什么好处,如果他给一个余额不足的交易通过认可,这样他自己的交易永远都不会被验证成功。
为了要认可Alice 的这笔交易,Charlie 必须列出所有Alice 这笔交易,直接和间接认可过的所有交易,一直列到创世交易。然后就出现了下面这一个很长的列表
1. 创世交易创造了15i
2. 创世交易给Bob 2i
3. 创世交易给Alice 8i
4. 创世交易给Charlie 5i
5. Charlie 给Donna 3i
6. Bob 给Alice 2i
任何的过程只要结果是让Alice 有10i 而且Bob 有0i 都是可以接受的结果。而且Charlie 必须注意到所有其他帐号在这个系统里面帐户余额都不能是负数,如果是负数的话,Charlie 的交易就会是无效的。
接下来我们看看另一个例子。如果Alice 想要给Bob 超过他户头余额的IOTA数会发生什么事情。

如果Alice 给Bob 100i,但是Alice 只有10i。这样Alice 的交易,和接下来所有让Alice 交易认可成功的交易,都会被整个IOTA 网路视为无效交易。
整个状况会变得更有趣如果我们是认可了两笔交易而不是一笔交易(实际上一般状况下也需要认可两笔啦)。
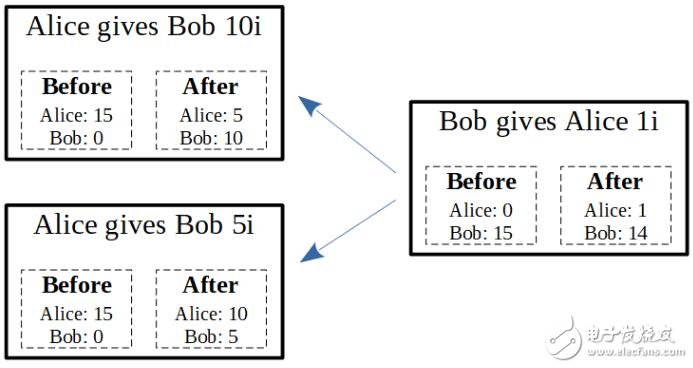
在右边Bob 付钱的交易,成功认可了左边两笔Alice 付钱的交易,因为Alice 的帐户余额是足以付那两笔交易的钱。
那如果余额不足怎么办? 下面这张图呈现了这个例子。在下面这个例子中Bob 不能让Alice 的交易被认可成功,因为如果认可成功的话,这样Alice 的帐户余额就会是负数的,而负数的帐户余额是不被允许的。如果Bob 让Alice 的交易认可成功,他就打破了IOTA 协议,在IOTA 网路上的所有人都不会让Bob 的交易被认可成功。
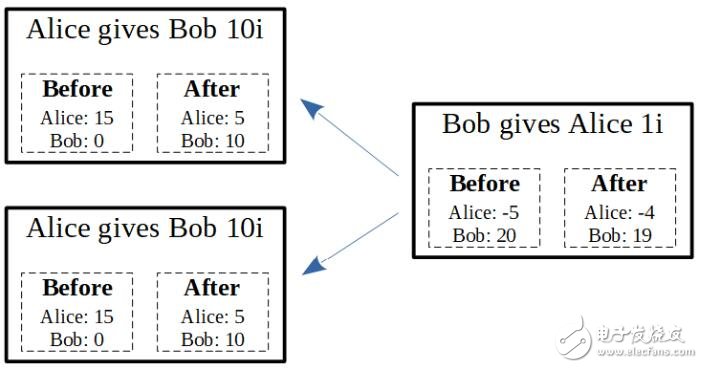
上面这个状况叫做双花(双重花费double spend),因为Alice 把他的钱花了两次。而且必须注意到,Alice 在他花费的当下没有破坏IOTA 协议,因为每一笔交易的当下,Alice 的帐户余额都足以支付当下那笔个别的消费。也许Alice 也不是故意做双花攻击,她只是不小心就送出了两笔交易的广播。反正结果就是,Alice 创造了两个分岔,这两个分岔在tangle 上没办法被整合。这样就造成一个大问题给所有的IOTA 诚实使用者: ”到底哪一笔交易才是能让他们认可成功的呢? “
这个问题的解决办法就是之前所提到的加权随机漫步( weighted walk)。最后这两个分支会有一个变成加权值比较大另一个比较小。之后的交易会接在加权值比较大的分支上(这个行为就像是交易被留下),加权值较小的会被放弃。这件事也暗示着,交易从被发出去到认可成功会有一段时间的延迟,即使有些交易成功认可了这笔刚发出去的交易,也不能保证这笔刚发出去的交易会不会是有冲突交易分岔上的一部份。为了确认这笔交易是不是被确认认可了(comfirmed)。我们必须等到这笔交易的确认信心( confirmation confidence )足够高,关于这些我们下面会进行解释。
在上面内容我们有提到,当Alice 多次花费或者多次广播交易时会造成双重花费的问题。我们下面来介绍在tangle 上会如何解决这个问题,还有如何片段哪一个交易历史才适合的交易历史。
为了阐明这个问题,我们将会检视下面这个双花的情境。
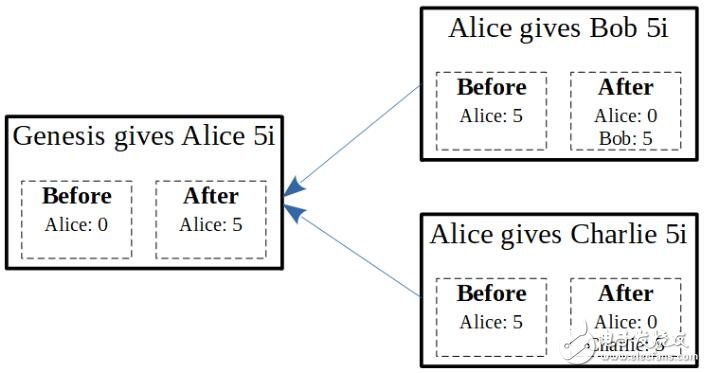
如你所见,Alice 在最一开始有5i。在接下来的交易,Alice 把这5i 同时给Bob 还有Charlie两个人,也就是说他重复花费了这5i。这很明显的是一个问题! 即便这两笔交易都是合法的,但是我们如果让两笔交易都合法的话就会让Alice 多给了不存在的5i。用tangle 的术语来说,我们没办法让未来的交易同时认可(approve)这两笔交易,因为这样会造成Alice 帐户余额是负数。
前面的文章告诉我们,透过加权随机漫步演算法,在上图最终会有一个分支加权值会大得多。因此共识(consensus)就会形成,然后加权值比较大的交易就会成为合法交易。但是从Bob 和Charlie 的角度,他们怎么知道他们真的从Alice 那边收到钱了呢?
想像一下Bob 和Charlie 都是恐龙贩售商(dinosaur dealer,这例子真贴近生活……),Alice 是一个恐龙狂粉,他跟这两个恐龙贩售商都买了一只暴龙。假如这两位贩售商一看到交易出现在tangle 上就瞬间寄出暴龙的友好店家。但这样的话,最终这两个好心店家会有一个人发现他没有收到钱。我们要如何不让友好店家们不会白白送人一只爬虫类动物呢?
这是一个非常严重的问,比特币是第一个成功解决这种问题的技术。为了示范tangle是如何解决这种问题,我们要介绍一个新概念叫”确认信心( confirmation confidence )“。这个信心是测量tangle上对于一个交易的接受程度(level of acceptance)。
信心程度是透过下列过程进行计算。
1. 跑端点选择演算法100 遍。
2. 记下有多少个交易认可我们这笔交易,并且记录下来叫A。
3. 这个交易的确认信心( confirmation confidence )就是A percent
换句话说,确认信心( confirmation confidence )就是认可这笔交易的端点百分比。并非所有端点都是给予相同程度的重要性,如果某个端点他有更高的机率被选取的话,那他在计算确认信心( confirmation confidence )时的重要性就会更高。为了呈现这点,我们把确认信心( confirmation confidence )加到模拟里面。在下图,拥有超过95%确认信心( confirmation confidence )的交易,我们以粗框方格表示。
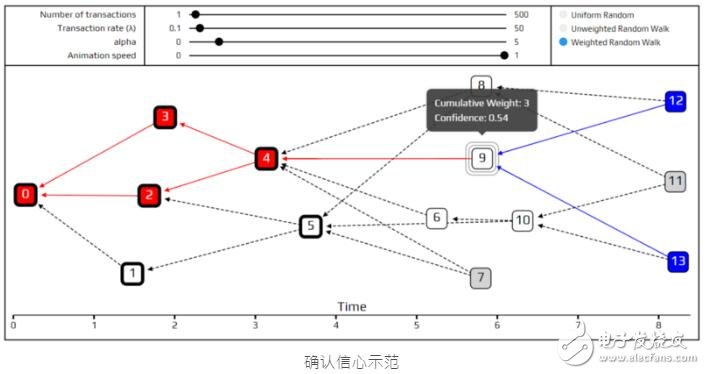
在上图,交易9 被4 个中的2 端点认可(交易12、交易13认可,交易11、交易7 不认可)。如果我们用机率一致的端点选取演算法,交易9 会有50% 的确认信心。然而,认可交易9 的端点们明显的比没有认可交易9 的端点们有更高一点的可能性,因此这提升了一点交易9 的确认信心。
现在要让Bob 和Charlie 判断何时出货Alice 订的暴龙变得明确许多。只要Alice 的交易超过某个非常高的信心水平,比如说95%,这样这笔交易被推离共识,认为是非法交易的可能性就会变得很低。但是我们必须说”可能性变得很低“,而不是说”不可能“。如果Alice 是坏蛋,而且他拥有足够的算力,他还是能够成功的执行双花攻击。
为了执行双花攻击,Alice 会新发布一个付钱给Charlie 而非给Bob 的交易。Alice 必须用这个给Charlie 的交易认可两个旧的交易,而这两个旧的交易不可以参考到给Bob 的那个交易(原文写给Charlie 的交易,但是我觉得怪怪的感觉是给Bob 的交易才能双花)。接下来他会一直送出超级大量新的交易,去让这个给Charlie 钱的交易(分支)有更高的累积加权值。如果Alice 拥有足够巨大的算力,就可以让整个IOTA 网路相信Alice,并且把之后自己的交易接在这个新的分支后面。因此Alice 成功的翻转了历史纪录,成功实行了双花攻击。在这个时候,如果我们去看给Bob 钱的交易的确认信心,我们会发现,给Bob 钱交易的确认信心从95% 掉到趋近于0,甚至是0。
攻击如下图所示,越往下时间越后面。
这种情境只会在Alice 拥有超过,或者接近整个IOTA 网路算力时才会发生,也就是说Alice 能够发送超过或接近整个IOTA 网路其他人送出的交易数总和。因此对于一个成熟而且足够活跃的网路来说,这是不用担心的。但是对于现在的IOTA 网路而言,这会是一个很大的问题。现在IOTA 网路的交易量还不足以抵抗双花攻击。
因为IOTA 本身的设计就有可扩充性,所以IOTA Foundation 设计了一个暂时的志愿性质的共识机制。这个机制就是协调员(coordinator)。每两分钟(印象中这数字现在有改变)就会有一个里程碑交易(mileston transaction)被IOTA Foundation 发布出来。所有被里程碑交易认可的交易的确认信心都会直接被提升到100%。透过协调员,Alice 的交易就永远不会被认可。我们采用这个方式去保护现在还不成熟的IOTA 网路,直到IOTA 网路足够活跃到能够转移到100% 去中心化,应用整个完整的IOTA 分散式共识演算法。在这个时候IOTA Foundation 就会关掉协调员,让tangle 自己成长。到那个时候,移掉协调员也可以让整个网路有几个数量级的加速。
 电子发烧友App
电子发烧友App


















评论