Grin,一种使用MimbleWimble协议的新型加密货币,连日来让整个市场为之兴奋。但其相关教程却乏善可陈。
Grin输出采用了Pedersen Commitment。输出形式如下:
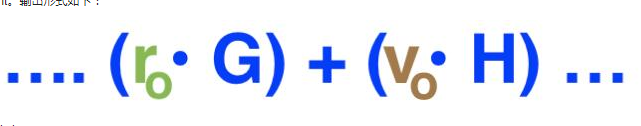
Grin输出——Pedersen Commitment方案。
Pedersen Commitment是一种隐藏信息的巧妙方式。如果这是你第一次听到Commitment,那么再看到这个词语的时候你就可以将其理解为“隐藏价值”。
如果我们选择一个非常大的数字 k 作为私钥,则k * H被认为是相应的公钥。即知道公钥k * H的值,要推导出 k 的值也几乎是不可能的。..
• r 是私钥,用作盲因子, G 是椭圆曲线上的不动点,他们的乘积 r*G 是曲线上r的公钥。
• v 是输入或输出值,H 是椭圆曲线上的另一个不动点。
在公式(k + j)* H = k * H + j * H中, k 和 j 都是私钥,说明两个私钥和获取的公钥(k + j)* H,等于每个私钥的对应公钥和(k * H + j * H)。
在ECC入门中有对密码学更深入的研究,但简而言之,要花费Grin,就必须要知道盲因子(r)和Grin的数量(v)。而要解构commitment来推断这些值是不可能的。我们必须提前知道这些值。
盲因子之所以存在是因为向你支付Grin的人也知道v的值是多少(他们向你发送了多少Grin)。但只有你(而非Grin的发出方)知道该输出的盲因子,因此,只有你能够花掉这笔输出。
假设该笔输出使用的盲因子为20,且该笔输出包括40个Grin。(注:Grin的数量实际上是以原子单位1 NanoGrin的倍数发送的。简单起见,这里我们使用“Grin”来表示。):
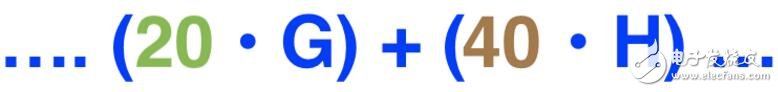
该笔输出中,盲因子为20,Grin数量为40.
若查看Grin的区块链浏览器,你会发现这笔输出不会如上所述整齐地分解。以下为真正的Grin输出,与我们所创建的一样:

Grin输出形式(在Commit列下)
同样,要从该输出中推导出“20”(盲因子)或“40”(Grin数量)是不可能的。
花费输出
假设我们展示的输出属于Alice。现在,Alice希望将40个Grin中的25个发送给Bob。为方便说明,我们将忽略矿工费。
如果你用一张5美元的钞票买了一件3美元的东西,那么你会得到2美元的找零(余额)。比特币交易方式亦是如此,Grin也不例外。如果Alice想要从她未使用的40个Grin输出中发送25个Grin给Bob,她也会在同样一笔交易中创建一个输出,这笔输出会将余下的15个Grin(找零)返还给她自己。
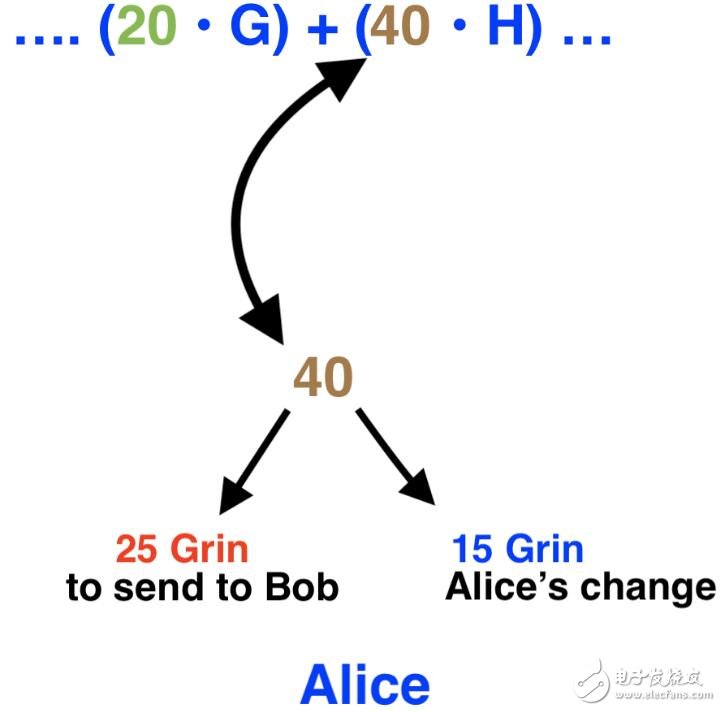
Alice确定想要发送给Bob的Grin数量,及其余额。
这15个Grin将回到Alice的账户中,这就意味着,只有她能够控制并再次花费。换言之,Bob无法花费Alice的这15个找零。为此,Alice必须为这15个找零创建一个新的盲因子。假设Alice选择34作为盲因子。
Alice既知道r值(找零输出的盲因子),也知道v值(余下Grin数量)。这样,她就拥有了创建找零输出(co)所需的一切信息。这也将作为一笔输出记录在区块链上,就像Alice很快生成的、将25个Grin发送给Bob的输出一样。

Alice的余额输出。
如前所述,要花费任何一笔输出,必须知道输出中所使用的盲因子。Alice知道她想要花费的输出中所使用的盲因子(20),但她需要一种方式向所有人证明她知道。
为此,她需要创建一个完全独立的计算方法——盲因子总和。这里需要Alice用她刚刚为自己的余额输出创建的盲因子(34),减去她希望花费的输出的盲因子(20)。
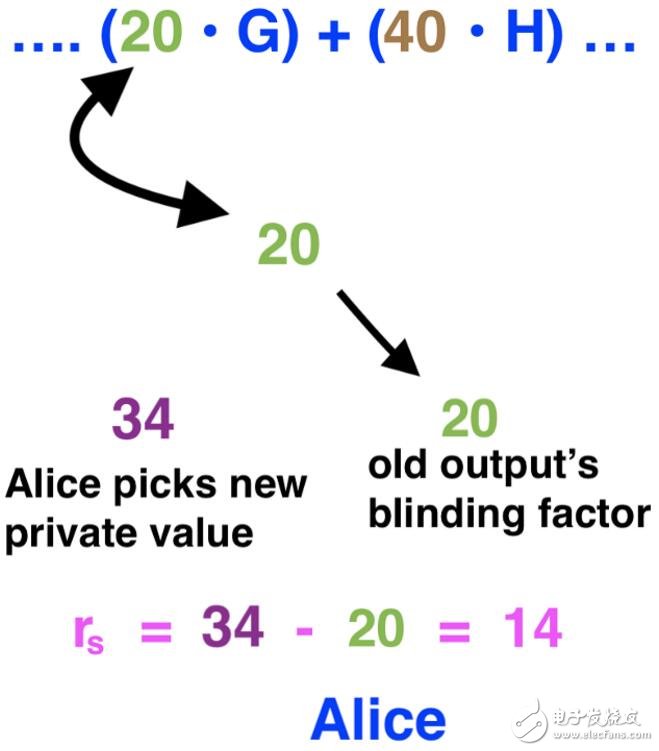
Alice的盲因子总和。
s(s代表发送方,即Alice)是Alice所有盲因子的总和,本例中总和为14。(注:本文中我有意忽略了内核偏移)。
最后,Alice要创建一个随机数ks(s同样代表发送方)。她将使用该随机数为这笔交易构建签名,我们将在稍后展示签名的构建过程。Alice不会将实际随机数发送给Bob。相反,她发送的是ks • G,这是对该随机数的承诺(commitment)。如前所述,Alice将随机数与生成点G相乘,从而隐藏了实际随机数的值。
Alice会将以下信息发送给Bob。但实际上,Grin数据并未被分为“元数据(Metadata)”和“数据(Data)”字段。而为了清晰起见,我们在这里会按照如下形式表示。
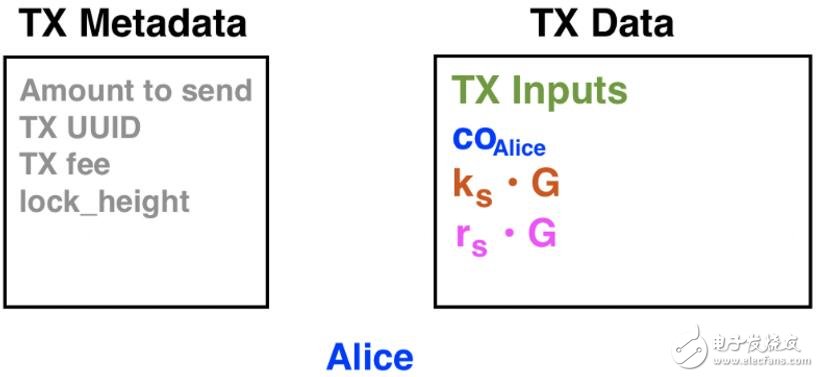
Alice在本次Grin交易的第一步中发送给Bob的所有信息。
元数据字段包括:
1. 发送数量:Alice想要发送给Bob的Grin数量(本例中为25)。
2. TX UUID:Alice和Bob在来回发送数据时用于标识此交易的唯一标识符。
3. TX fee: 交易费用(本教程中将不予讨论)。
4. 区块高度(lock_height):该笔交易生效时的区块编号。
数据字段包括:
1. TX输入:未花费的输出,Alice用作与Bob进行交易的输入。
2. co: Alice的余额输出。
3. ks • G: Alice的随机数ks乘以生成点G,成为对该随机数的承诺。
4. rs • G: Alice所有盲因子rs的总和乘以生成点G,成为对该值的承诺。
Alice将以上全部数据发送给Bob,Bob继续下一步操作。
轮到Bob
Bob在接收到Alice发来的数据后,将交易费用(TX fee)和区块高度(lock_height)变量联系起来以创建M,我们称之为该笔交易的“信息(Message)”。

该笔交易的“信息”
Bob为他想要从Alice那里收到的25个Grin选择一个盲因子rr(r代表接收方,在本例中为Bob)。假设他选择11作为盲因子rr,同时还选择了自己的随机数kr(r同样代表接收方)。
正如Alice所做的,Bob也分别将这两个值乘以生成点G,创建对这两个值的承诺。接着Bob利用这些数值,为该笔交易生成Schnorr challenge,由变量e表示:
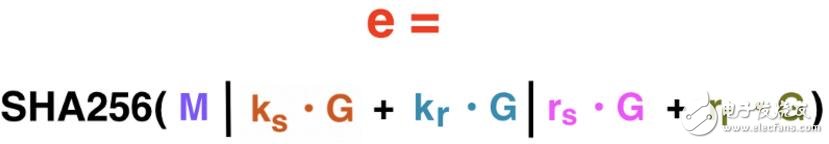
该笔交易的Schnorr challenge。
Schnorr challenge按顺序包含以下内容的SHA256哈希:
1. 交易信息。
2. Alice和Bob使用随机数的承诺总和。
3. Bob(25个Grin输出)的盲因子承诺总和,和Alice所有的盲因子总和。
Bob使用e为交易生成他的Schnorr签名,sr(r代表接收方)。虽然这是Bob签名的全部内容,但我们称之为Bob的部分签名,因为它最终将与Alice的部分签名相加,从而得到整个交易的签名。
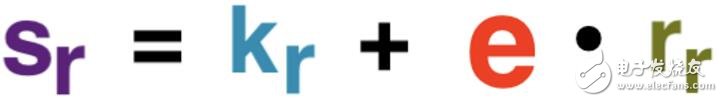
该笔交易Bob的部分签名
当Alice最终收到sr时,她是无法从中得知kr或rr的值的。
Bob将以下内容发回给Alice:
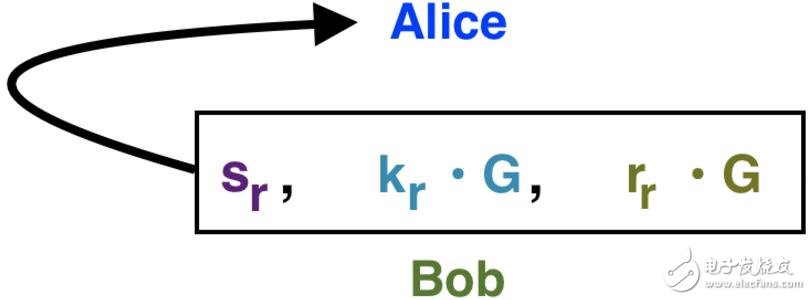
Bob将他的部分签名、随机数承诺以及对输出盲因子的承诺发回给Alice。
这些内容按顺序包括:
1. sr: Bob的部分签名。
2. kr • G: Bob的随机数承诺
3. rr • G: Bob对他想要得到的25个Grin的盲因子承诺
最后一步:回到Alice
Alice现在拥有所需一切信息,可以在本地计算e,即该笔交易的Schnorr challenge。在本地计算了e之后,Alice可以验证Bob的部分签名。
Bob的部分签名sr包含以下内容:
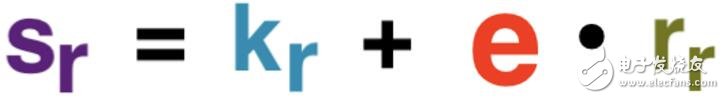
该笔交易Bob的部分签名
基于我们前面描述的椭圆曲线的性质,Alice可将生成点G引入方程式两边,等式仍然成立。

Alice将等式两边分别乘以生成点G。
由于Alice收到了Bob的kr•G(Bob的随机数承诺)和rr•G(Bob的盲因子承诺,他将使用该盲因子来获得他将收到的那25个Grin),同时由于已经在本地计算了e,Alice可以简单地乘以生成点G,并确保等式的右边等于这个值,从而验证Bob的部分签名sr。
如此,Alice便证明了:
1. Bob知道他会收到多少Grin(25个)。
2. Bob知道其随机数。
3. Bob知道他想要得到的25个Grin的盲因子。
而Alice不会知道Bob选择的随机数或者盲因子。
接着,Alice生成自己的部分签名:
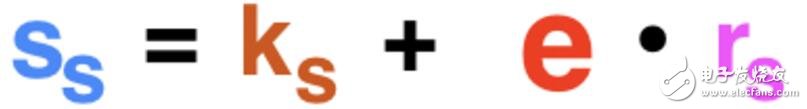
Alice为该笔交易生成部分签名。
Alice现在可以生成交易的签名,其中包括Alice和Bob的部分签名:

交易签名,包括Alice和Bob部分签名的总和以及对其随机数的承诺。
签名按顺序包括:
1. Alice和Bob部分签名的总和。
2. Alice和Bob的随机数承诺的总和(他们彼此互不知道对方的真实随机数)。
简化后该签名表现为:
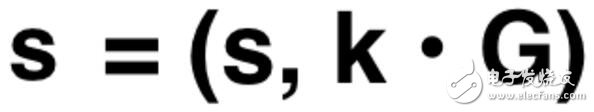
该交易的签名
其中 s = ss + sr, k = ks + kr.
记住这个签名,很快你就会理解它的意义。
完成交易
数字货币需要“记忆”——也就是说,当你将一笔钱发送给某一个人的时候,你就不能将它再发送给另一个人。而Grin的运作方式隐藏了发送的Grin数量和接收方。那么,我们怎么能证明一笔钱没有被重复支付或凭空创造出来呢?
在一笔Grin交易中,当从输入中减去所有输出时,剩余Grin的数量应该等于0。那么回到之前的5美元例子:
给收银员3美元(输出) + 2美元找零返还给我 (输出) – 5美元纸钞 (输入) = 0
在Grin的交易中,当一笔交易合法时,相同的求和使得v值总和为零。但我们如何在不展示这些数值的情况下证明这一点呢?让我们看看从Alice到Bob的交易中使用的输入和输出:
(34•G) + (15•H) + (11•G) + (25•H) - (20•G) - (40•H) = (25•G) + (0•H)
这里的巧妙之处在于,当Grin的数量抵消时(不存在凭空创造的情况下应该得到的结果),从输入减去输出所剩下的就是“过多盲因子(the excess blinding factor)”的承诺,或“kernel excess”。本文例子中,盲因子的承诺是25•G,是曲线上的公钥。
如果一笔Grin交易的输出总和减去输入总和会在曲线上产生一个有效公钥,那么你就会知道,v值一定已经被抵消了。如果对于某个已知的n值,等式的右边不是n•G + 0•H的形式,那么该笔交易无效。这意味着要么花费的金额大于输入的总和(就好比你拿出5美元纸钞,向收银员支付3美,却得到找零10美元),要么输入大于输出(就好比你拿出5美元纸钞,向收银员支付3美元,却没有找零)。
还记得这个签名吗?
该交易的签名
这个签名实际上已经对我刚刚提到的过多盲因子签署了承诺。以下对此进行了阐释。
如果你还记得的话,这就是当你在等式两边同时乘以生成点G时,Bob的部分签名。
当两边同时乘以生成点G时,Bob的部分签名。
同样,以下为等式两边同时乘以生成点G后,Alice的部分签名。
等式两边同时乘以生成点G后,Alice的部分签名。
如果将两个方程式相加会发生什么? 你会得到:
sr•G + ss•G = (kr • G) + (ks • G) + (e • (rr•G + rs•G))
记住,rr是Bob的盲因子,rs是Alice的盲因子之和。前面提到的rr•G + rs•G等同于(rr + rs)•G。
Bob对其盲因子的承诺是11•G。Alice对其盲因子总和的承诺是14•G。二者相加,得到25•G,这就是对交易中过多盲因子的承诺。因此,加上sr和ss (Bob和Alice各自的部分签名)就证明了整个交易的有效性,因为它们加起来就等于对过多盲因子的承诺。
进一步简化该等式,我们会得到:
sr•G + ss•G = (k•G) + (e • (r•G))
或:
sr•G + ss•G = (k•G) + (e • (25•G))
接下来就要检查左右两边是否相等。
记住,这个等式中的所有内容(部分签名的总和,e中的所有内容,对过多盲因子的承诺,对随机数总和的承诺)都是公开可见的,因此任何人都可以对此进行验证。我们既不需要Alice也不需要Bob的盲因子来验证交易。加上他们的部分签名,并验证他们对过多盲因子的承诺进行了求和,我们就证明了:
1. 在花费Alice之前的输入时,没有凭空创造新的资金。
2. Alice和Bob在创建该笔交易时都知道其输出的盲因子。这意味着他们可以花费新的输出,不会出现问题。
我们用来验证交易的信息被放在交易内核中。
交易内核
除输出外,交易内核是从Grin交易输出中得到的另一条信息。每笔交易都会生成一个交易内核,但是Grin区块链是无法查看的,也无法将一笔输出与交易内核相关联。每笔Grin交易都存在一个交易内核,其中包含了“没有凭空创造新的资金”的证明。
交易内核中存储信息如下:
1. 交易的签名(s, k • G)。
2. 与“过多盲因子”相关的公钥(在本例中为25•G)。如上所述,可用其验证s。
3. 交易费和交易的区块高度。(注:如果是Coinbase交易,则这两者均不存在)。
总结
完成以上操作后,从该笔交易向网络中广播的信息仅包括:
1. 使用的输入。
2. 新的输出。
3. 交易内核。
4. 内核偏移。
 电子发烧友App
电子发烧友App



















评论