一、有功功率
无源二端网络 N 中含有线性电阻、电容、电感、受控源等元件，阻抗为 
。其端电压和端电流分别为 
。
二端网络 N 吸收的瞬时功率为
平均功率（ average power ）是指在一个周期内吸收的瞬时功率的平均值，用 P 表示，即
有功功率
在一个周期内吸收的瞬时功率的平均值，称为平均功率，又称有功功率（ active power ），单位为瓦（ W ）。
有功功率是真正由来做功的功率，由网络中的电阻元件产生。 
称为二端网络的功率因数（ power factor ）， 
又称为功率因数角。
二、无功功率和视在功率
无功功率
无功功率表示网络与电源进行能量交换的规模，由网络中的储能元件产生。单位是乏（ var ）。
视在功率
单位是伏安（ VA ）。
设二端网络的等效阻抗为
则该二端网络的等效电阻为
该二端网络的等效电抗为
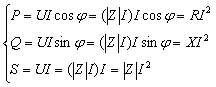
图 7.5-1 中， 
，则 
， 
，根据各功率的定义，可以得到
1 、电阻元件， Z=R ， 
， 
，则
电阻元件只从电路中吸收能量，而不与电路作能量交换；
2 、电感元件， 
， 
， 
，则
电感元件不耗能，只与电路作能量交换；
3 、电容元件， 
， 
， 
，则
电容元件也不耗能，只与电路作能量交换。
三、复功率
复功率
二端网络的端电压为 
，端电流为 
，设端电流的共轭相量为 
，则定义 
和 
的乘积为复功率（ complex power ），即
功率守恒
如果二端网络中含有 n 个元件，则有功、无功、复功率都守恒
但是，视在功率不守恒
例 7.5-1 图 7.5-2 所示电路中， 
，角频率 
， 
，电路吸收的有功功率 P=200W ，求电阻 R 和电感 L 。
 |
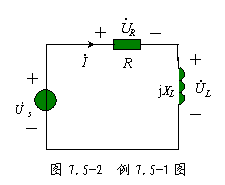解：由 KVL 可得
所以，
因为电路吸收的有功功率就是电阻 R 吸收的有功功率，即
所以，电阻
又
则感抗为
所以，电感
例 7.5-2 图 7.5-3 所示正弦稳态电路中，已知电压源 
，电流源 
，试分别求出电压源和电流源发出的总有功功率。
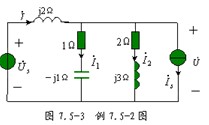
解：根据功率守恒性，电压源和电流源所发出的总有功功率，就是 1 Ω和 2 Ω电阻吸收的有功功率之和，因此，只要先求出通过 1 Ω电阻的电流 
和通过 2 Ω电阻的电流 
就可以了。
设电流源两端的电压为 
，列写节点电压方程，
代入参数，得
解得
所以
因此，电压源和电流源发出的总有功功率为
四、最大功率传输
一个含源的二端网络，总可以用一条电压源 
和等效阻抗 Zo 相串联的戴维南等效支路来替代，如图 7.5-4 所示。
 |
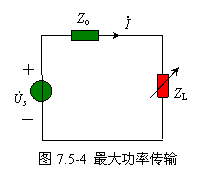设电压源的等效阻抗为 
，负载阻抗为 
。
则电路中的电流
电流的有效值为
负载 
获得的有功功率实际就是 
中的电阻部分 
获得的有功功率，所以，负载获得的功率为
1 、负载 
的电阻部分 
和电抗部分 
皆可调
式中， 
，欲使 PL 达到最大，可先令 
，即 
，这时，
再调节 RL ，使 PL 达到最大，令 
，即
解得：
因此，当负载阻抗与电源等效阻抗互为共轭复数， 
时，即
负载获得最大功率，称为共轭匹配（ conjugate matching ）。这时获得的最大功率为
2 、负载 
的阻抗角 
固定，而阻抗模 
可变
有些情况下，负载是电阻性设备，即 
， 
，这时， 
， 
，通过调节 RL 使负载获得最大功率。
负载获得的功率为
令 
，即
解得：
当负载为一个电阻时，负载获得最大功率的条件是负载电阻与电源等效阻抗的模相等，即模匹配（ modular matching ）。
模匹配时负载电阻获得的最大功率为
结 论
1 、当负载 
和 
皆可调时，采用共轭匹配
， 
2 、当负载为纯电阻 
时，采用模匹配
， 
3 、一般情况下，负载在模匹配时获得的最大功率比共轭匹配时要小。
例 7.5-3 电路如图 7.5-5 所示， 
，负载为以下两种情况：（ 1 ）负载 
为可变电阻，（ 2 ）负载 
为可变阻抗（ RL 、 XL 均可调），试问负载分别为何值时获得最大功率，并求最大功率值。
 |
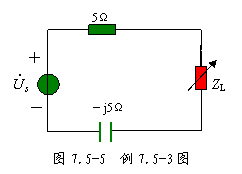解： 电压源的等效阻抗为
（ 1 ）负载为可变电阻时，欲使负载获得最大功率，则应采用模匹配，
，即负载 ZL=RL=7.07 Ω时获得最大功率，最大功率为
（ 2 ）负载为可变阻抗，即 RL 、 XL 均可调时，欲使负载获得最大功率，则应采用共轭匹配，
，即负载 
时获得最大功率，最大功率为
，显然，负载采用共轭匹配时获得的最大功率比采用模匹配时要大。