第2节 卫星的无摄运动

3.2.1卫星运动的轨道参数

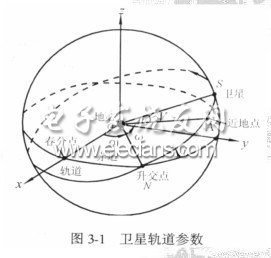
卫星的无摄运动可由一组经过选择的具有鲜明几何意义的轨道参数来描述，它们是：

Ω——升交点赤经。

i——轨道面倾角。

a——卫星轨道为椭圆。

e——卫星轨道为椭圆。

ω——近地点角距。

M——平近点角。

  以上六个轨道参数，前5个是常数，不随时间变化而改变，大小由卫星发射条件所决定。

  卫星S围绕地球质心O的运动关系如图3-1所示。

3.2.2二体问题的运动方程

在图3-1中所示的二体问题中，依据万有引力定律可知，地球O作用于卫星S上的引力F为：

式中：G——万有引力常数，G=(6672±4.1)×10^-14 N·m²/kg² ；

      M,m——地球和卫星的质量；

      r——卫星的在轨位置矢量。

由牛顿第二定律可知，卫星与地球的运动方程：

设以O为原点的直角坐标系为O-XYZ，S点的坐标为（X，Y，Z），则卫星S的地心向径r=（X，Y，Z），加速度，代入（3-4）得二体问题的运动方程：

3.2.3二体问题微分方程的解

1、卫星运动的轨道平面方程

直接由微分方程（3-6）求积分，可得卫星运动的轨道平面方程：

2、卫星运动的轨道方程

卫星运动的轨道方程为：

3、用偏近点角E代替真近点角V

由表示偏近点角E与真近点角V的关系的图3-2，不难证明:

4、开普勒方程

设卫星的运动周期为T，则卫星平均角速度为：