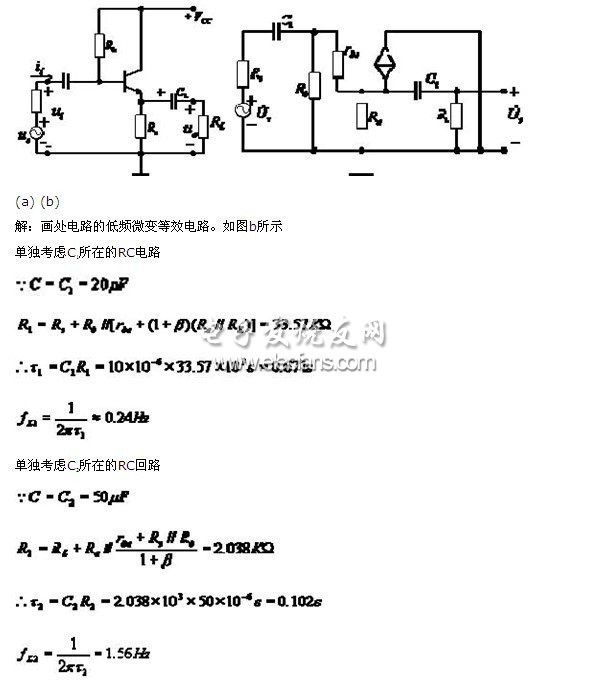
3.3 共e极放大电路的频率特性
(1) 共e极放大电路及其混合π型等效电路
具体分析时, 通常分成三个频段考虑:
(1) 中频段: 全部电容均不考虑, 耦合电容视为短路, 极间电容视为开路。
(2) 低频段: 耦合电容的容抗不能忽略, 而极间电容视为开路。
(3) 高频段: 耦合电容视为短路, 而极间电容的容抗不能忽略。
这样求得三个频段的频率响应, 然后再进行综合。 这样做的优点是, 可使分析过程简单明了, 且有助于从物理概念上来理解各个参数对频率特性的影响。
下面分别讨论中频,低频,高频时的频率特性。
- 一. 中频放大倍数Ausm
由图(2),可得
(2)中频段等效电路
由上述关系代入Uo的表达式中,得
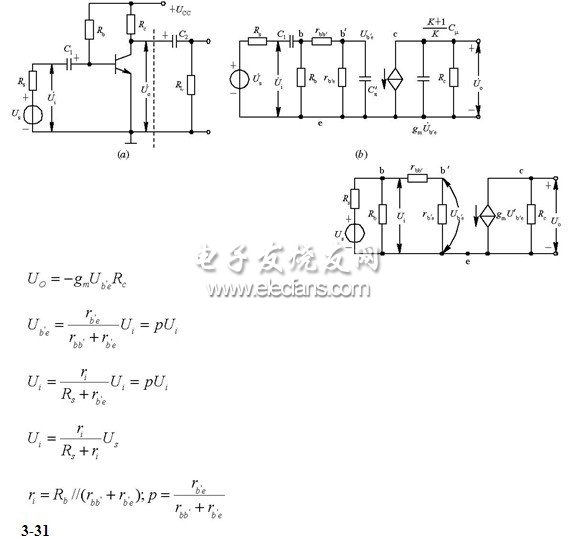
二.低频放大倍数Ausl及波特
由图(3),可得
3.32
(3)低频段等效电路
式中p、ri同中频段的定义。将 、 代入式3-32, 得 U?U?
将公式(3 - 31)代入, 并令
3-33
AAA11==?
3-34

将式(3 - 34)分别用模和相角来表示:
3-35 201
3-36
根据公式(3 - 35)画对数幅频特性, 将其取对数, 得
3-37
先看式(3 - 37)中的第二项, 当f>>fl时
故它将以横坐标作为渐近线;当f<<fl时
其渐近线也是一条直线,该直线通过横轴上f=f1这一点,斜率为20db/10倍频程。
(4)低频段对数频率特性
低频段的相频特性, 根据式(3 - 36)可知,

当f>>fl时, 趋于0, 则φ≈-180°; 当f<<fl时, 趋于90°,φ ≈-90°;当f=fl时, , φ =-135°。 这样可以分三段折线来近似表示低频段的相频特性曲线, 如图(4)(b)所示。 farctanfarctan=45arctanf
f≥10fl时, φ =-180°
f≤0.1fl时,φ =-90°
0.1fl<f<10fl时, 斜率为-45°/10倍频程的直线。
可以证明, 这种折线近似的最大误差为±5.71°, 分别产生在0.1fl和10fl处。
三.高频电压放大倍数Aush及波特图
由图(1),可得
(1)高频等效电路
由等效电路可求得 则 U
3-38 (2) 简化等效电路
为求出 与 的关系, 利用戴维宁定理将图(1)进行简化, 如图(2)所示, 其中 UsU
由图(2),可得

代入3-38式,得
令
上限频率为
则 A?
usmushAA=?
高

四
围内的放大倍数的表达式

频率大与单级放大器的下限频率。
由前面的各级放大电路总的电压放大倍数,是各级放大倍数的乘积。即 ?
nuuuuAAAA????=21
中在上、 下限频率处数707.0707.0ushushAAAA????===
而
ushAA=
ffhbw=
二可
1111
下
多
时
ffff,≈≈
例
例1 某放大电路在低
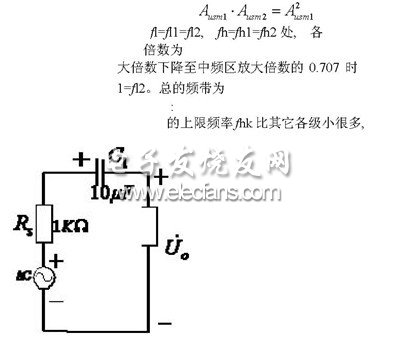
解: