计数器是时序电路也是数字系统中使用最多的电路形式,分类的方法也较多。按计数脉冲触发方式可分为同步和异步两大类;按计数制分类分为二进制、非二进制(包括十进制及其他任意进制)两类;按计数过程中的数值的增减分类可分为加法、减法、可逆计数器。这些分类又交叉重叠,因而计数器的种类名称较多。计数器不仅用于对时钟脉冲计数,还可以用于分频、定时、产生节拍脉冲和脉冲序列以及进行数字运算等等。
下面我们讲计数器是按计数器中的数字的编码方式分类,如二进制计数器、二—十进制计数器等。
一、 二进制计数器
1. 异步递增二进制计数器
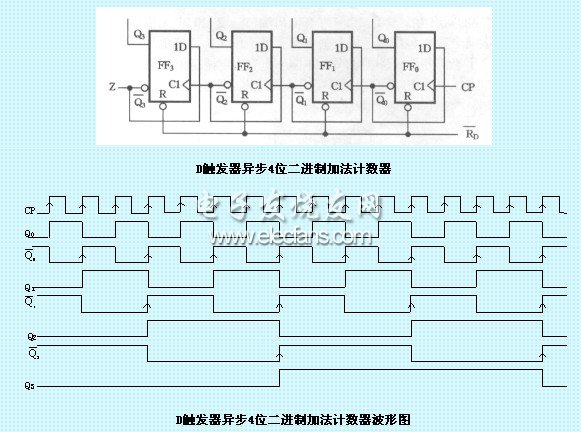
递增计数器就是每输入一个脉冲就进行一次加1运算,而二进制计数是输入脉冲个数与自然二进制数有对应关系。异步计数器是在做加1计数时是采取从低位到高位逐位进位的方式工作的。因此其中的各个触发器不是同步翻转的。按照二进制加法计数规则,每一位如果已经是1,则再计入1时应变为0,同时向高位发出进位信号,使高位翻转。若使用下降沿动作的触发器(此时该触发器应接成计数状态,例如JK触发器使J=K=1)组成计数器,只要将低位触发器的Q端接到高位触发器的时钟输入端即可。当低位由  时,Q端的下降沿正好可以作为高位的时钟信号CP。那么一个四位异步递增二进制计数器就如下图:
时,Q端的下降沿正好可以作为高位的时钟信号CP。那么一个四位异步递增二进制计数器就如下图:

JK触发器异步4位二进制加法计数器
分析:
(1)J、K接1,即四个触发器均处在计数状态
(2)清零端给一个负脉冲,进行总清,防止过去状态干扰输出
(3)画波形图

JK触发器异步4位二进制加法计数器时序图
从以上分析可以看出,各触发器的变化是依次逐个进行的,而每个触发器的变化都需要一定的延迟时间,尤其计数器位数教多时,累计延迟时间就教长,所以异步计数器比同步计数器的速度低。要可以用一个Z表示进位输出,也就是记满1111后次态为0000此时不同于总清的0000。
从波形上可以看出,每经一级触发器输出的脉冲的周期就增加一倍,即频率降低一倍,因此一位二进制计数器就是一个二分频器。
异步4位二进制加法计数器状态转移表

当触发器的个数为N时,最后一个触发器输出的频率将降为输入脉冲频率的1/2N,它能累计的最大脉冲个数为2N-1。例如我们前面画的图N=4,它就能累计15个脉冲而Q3输出1/16分频。如果使用上升沿触发器构成异步二进制递增计数器,其逻辑图:
综上所述,对一个二进制递增计数器归纳如下:
u 计数器由若干个工作在计数状态时的触发器构成。如用负跳变触发器则进位信号从  端引出;用正跳变触发器构成则进位信号则从
端引出;用正跳变触发器构成则进位信号则从  端引出
端引出
u N个触发器具有  个状态,称为以
个状态,称为以  为模的计数器(或模
为模的计数器(或模  计数器),其中计数容量为
计数器),其中计数容量为  -1
-1
u 由于异步计数器进位信号象波浪一样推进,因此又称为纹波计数器
2. 异步二进制递减计数器
按照二进制减法计数规则,递减计数器规律:若低位触发器已经为0,则再输入一个减计数脉冲后应翻转成1,同时向高位发出借位信号,使高位翻转。
|
CP数 |
Q2 |
Q1 |
Q0 |
|
0 |
0 |
0 |
0 |
|
1 |
1 |
1 |
1 |
|
2 |
1 |
1 |
0 |
|
3 |
1 |
0 |
1 |
|
4 |
1 |
0 |
0 |
|
5 |
0 |
1 |
1 |
|
6 |
0 |
1 |
0 |
|
7 |
0 |
0 |
1 |
|
8 |
0 |
0 |
0 |
如果用下降沿触发的JK触发器构成异步二进制减法计数器,则:

下降沿动作的异步二进制减法计数器

将异步二进制减法计数器与异步加法计数器比较可以看出,它们都是将低位触发器的一个输出端接到高位触发器的时钟输入端而组成的。在采用下降沿触发的计数器时,加计数以  端为输出端,而减法计数以
端为输出端,而减法计数以  端为输出端。可以推导,若采用上升沿计数器则情况相反。
端为输出端。可以推导,若采用上升沿计数器则情况相反。
3. 同步二进制递增计数器
异步计数器工作速度较低,常常又被称为串行计数器。为了提高计数述速度,可采用同步计数器,其特点是计数脉冲同时接于各位触发器的时钟脉冲输入端,当计数脉冲到来时,应该翻转的触发器同时翻转,没有各级延迟时间的积累问题。同步计数器又称并行计数器。
假设要组成四位二进制(M=16)的同步递增计数器,首先根据计数规律得到状态表:
|
CP序号 |
Q3 |
Q2 |
Q1 |
Q0 |
等效十进制数 |
|
0 |
0 |
0 |
0 |
0 |
0 |
|
1 |
0 |
0 |
0 |
1 |
1 |
|
2 |
0 |
0 |
1 |
0 |
2 |
|
3 |
0 |
0 |
1 |
1 |
3 |
|
4 |
0 |
1 |
0 |
0 |
4 |
|
5 |
0 |
1 |
0 |
1 |
5 |
|
6 |
0 |
1 |
1 |
0 |
6 |
|
7 |
0 |
1 |
1 |
1 |
7 |
|
8 |
1 |
0 |
0 |
0 |
8 |
|
9 |
1 |
0 |
0 |
1 |
9 |
|
10 |
1 |
0 |
1 |
0 |
10 |
|
11 |
1 |
0 |
1 |
1 |
11 |
|
12 |
1 |
1 |
0 |
0 |
12 |
|
13 |
1 |
1 |
0 |
1 |
13 |
|
14 |
1 |
1 |
1 |
0 |
14 |
|
15 |
1 |
1 |
1 |
1 |
15 |
|
16 |
0 |
0 |
0 |
0 |
0 |
分析状态表,可以得到各触发器的翻转条件
u 最低位触发器FF0每输入一个脉冲翻转一次
u 其它各触发器都是在所有低位触发器的输出端全为1时,在下一个CP有效沿到来时状态改变一次。
由于同步计数器中各触发器的CP端输入同一时钟脉冲,因此触发器的翻转状态就由它们的输入信号状态决定。例如JK触发器状态就由J、K端的状态决定。组成同步计数器的关键就是根据翻转条件,确定各触发器输入端的逻辑表达式。
如果用下降沿触发的JK触发器组成上述计数器,根据JK触发器的逻辑功能和上述两个条件,可列出四位同步二进制递增计数器各触发器之间的连接逻辑关系:
|
触发器翻转条件 |
J、K端的逻辑关系 |
|
|||
|
FF0 |
每输入一个脉冲翻转一次 |
J0=J0=1 |
|||
|
FF1 |
Q0=1 |
J1=K1=Q0 |
|||
|
FF2 |
Q0=Q1=1 |
J2=K2=Q0Q1 |
|||
|
FF3 |
Q0=Q1=Q2=1 |
J3=K3=Q0Q1Q2 |
根据这些方程可以画出同步二进制递增计数器的逻辑电路图:

同步4位二进制加法计数器
对于同步二进制递增计数器也可以用状态图描述或工作波形(时序图)描述。

4位二进制加法计数器状态图

4位二进制加法计数器时序图
4. 二进制递减计数器
对于同步二进制递减计数器,首先要列写状态表,下面以4位二进制递减计数器为例
|
CP序号 |
Q3 |
Q2 |
Q1 |
Q0 |
输出Z |
|
0 |
0 |
0 |
0 |
0 |
1 |
|
1 |
1 |
1 |
1 |
1 |
0 |
|
2 |
1 |
1 |
1 |
0 |
0 |
|
3 |
1 |
1 |
0 |
1 |
0 |
|
4 |
1 |
1 |
0 |
0 |
0 |
|
5 |
1 |
0 |
1 |
1 |
0 |
|
6 |
1 |
0 |
1 |
0 |
0 |
|
7 |
1 |
0 |
0 |
1 |
0 |
|
8 |
1 |
0 |
0 |
0 |
0 |
|
9 |
0 |
1 |
1 |
1 |
0 |
|
10 |
0 |
1 |
1 |
0 |
0 |
|
11 |
0 |
1 |
0 |
1 |
0 |
|
12 |
0 |
1 |
0 |
1 |
0 |
|
13 |
0 |
0 |
1 |
1 |
0 |
|
14 |
0 |
0 |
1 |
0 |
0 |
|
15 |
0 |
0 |
0 |
1 |
0 |
|
16 |
0 |
0 |
0 |
0 |
1 |
分析状态可以总结:
u 低位触发器FF0每输入一个脉冲翻转一次
u 其它各触发器都是在所有低位触发器的输出为0时变化
仿效递增计数器,可得四位同步二进制递减计数器级间连接的逻辑关系:
|
触发器翻转条件 |
J、K端的逻辑关系 |
|
|
FF0 |
每输入一个脉冲翻转一次 |
J0=J0=1 |
|
FF1 |
Q0=0 |
J1=K1= |
|
FF2 |
Q0=Q1=0 |
J2=K2= |
|
FF3 |
Q0=Q1=Q2=0 |
J3=K3= |
根据逻辑表达式可以画出逻辑图:

同步4位二进制减法计数器
当然也可以用状态图和时序图描述该电路。
从上面分析可以发现,对于同步二进制计数器,递增和递减的区别在于J、K端来自低位触发器的输出为1还是0,那么通过一个控制端就可以实现可逆计数。
二、 8421BCD码十进制计数器
二进制计数器,虽然它的袋内陆结构简单,运算方便,但是当二进制数的位数较多时,要很快地读出来就比较困难,因此有讨论十进制计数器的必要。所谓十进制就是“逢十进一”。前面讨论四位二进制计数器的计数状态是从0000~1111共16个状态。要表示十进制的十个状态,就要去掉其中6个状态,至于去掉哪些可以有不同的安排,如果考虑BCD编码,即去掉1010~1111这6个状态。
下面给出用JK触发器组成的一位异步十进制递增计数器逻辑图

异步8421BCD十进制加法计数器
分析计数原理:

代入JK触发器的特性方程  可以写出
可以写出

画出时序图:

异步8421BCD十进制加法计数器时序图
按照同样的道理,可以分析8421BCD码同步十进制递减计数器。
事实上,画工作波形、列写状态方程、状态表是分析时序逻辑电路常用的方法,要仔细理解并掌握这些分析方法。




