1.3.1 真值与机器数
上述讨论的过程中都没有考虑二进制数的符号,一般认为其为正数,但在算术运算过程中,总会出现负数。实际上不带符号的数是数的绝对值,在绝对值前加上表示正负的符号(+/- )就成了带符号数。它可由两部分组成:一部分是表示数的符号,另一部分是表示数的数值。由于数的符号是一个具有正、负两种值的离散信息,所以它可以用一位二进制数来表示。通常是以0表示正数,以1表示负数。对于一个n位二进制数,如果数的第一位为符号位,那么余下的n-1位就表示数的数值部分。
一般,直接用正号“+”和负号“-”来表示符号的二进制数,称为符号数的真值。数的真值形式是一种原始形式,无法直接用在数字计算机中。但是,当将符号数值化之后,便可以在计算机中使用它了。因此在计算机中使用的符号数便称为机器数。
如二进制正数+1011在机器中的表示为01011,二进制负数-1011在机器中的表示为11011。
通过前面介绍的二进制数的加、减、乘、除四种运算可知,乘法运算实际上是做左移加法运算,而除法运算则是做右移位减法运算。即在机器中只需要做加、减两种运算。但在做减法运算时,必须先比较两个数绝对值的大小,再将绝对值大的数减绝对值小的数,最后在相减结果的前面加上绝对值较大的数的符号。因此,虽然逻辑电路可以实现减法运算,但所需的电路复杂,运算速度较作加法慢得多。为了能使减法运算变成加法运算,人们给出了三种机器数的表示形式,即原码、反码和补码。
1.3.2 原码
原码又被称为“符号—数值表示”。用当原码形式表示正数和负数的,第1位是符号位。对于正数,符号位表示的0,对于负数,符号位表示的1,其余各位表示数值部分。
假如两个带符号的二进制数分别为S1和S2,其真值形式为
S1= +11001 S2= -01011
则S1和S2的原码表示形式为
[S1]原= 011001 [S2]原= 101011
根据上述原码形成规则,一个n位的整数S (包括一位符号位)的原码一般表达式为
![]() (1.3.1)
(1.3.1)
对于定点小数而言,一般将小数点定在最高位的左边,此时,数值小于1。定点小数原码一般表达式为
![]() (1.3.2)
(1.3.2)
由原码的一般表达式中可以得出:
(1 )当S为正数时,[S]原和S的区别只是增加一位用0表示的符号位。由于在数的左边增加一位0对该数的数值并无影响,所以[S]原就是S本身。
(2 )当S为负数时,[S]原和S的区别是增加了一位用1表示的符号位。
(3 )在原码表示中,有两种不同形式的0,即
[+0]原= 0.00…0
[- 0]原= 1.00…0
1.3.3 反码
反码又称为“对1的补数”。当用反码表示时,左边第1位即为符号位,符号位为0代表正数,符号位为1代表负数。对于正数,反码和原码相同。而对于负数,反码的数值是将原码数值按位求反,即原码的某位为1,则反码的相应位便为0,或者原码的某位为0,反码的相应位便为1。所以,反码数值的形成与它的符号位有关。
假如两个带符号的二进制数分别为S1和S2,其真值形式为
S1= +1l001 S2= -01011
则S1和S2的反码表示形式为
[S1]反= 011001 [S2]反= 110100
根据上述的反码形成规则,一个n位的整数S (包括一位符号位)的反码一般表达式为
![]() (1.3.3)
(1.3.3)
同样,对于定点小数,如果小数部分的位数为m,则它的反码一般表达式为
![]() (1.3.4)
(1.3.4)
从反码的一般表达式可以看出:
(1 )正数S的反码[S]反与原码[S]原相同。
(2 )对于负数S,其反码[S]反的符号位为1,数值部分是将原码数值按位求反。
(3 )在反码表达式中,0的表示有两种不同的形式,即
[+0]反= 0.00…0
[-0]反= 1.11…1
1. 3. 4 补码
补码又称为“对2的补数”。在补码表示方法中,正数的表示同原码和反码的表示是一样的,而负数的表示却不相同。对于负数,将原码转变成补码的规则是:符号位不变,仍为l,数值部分变反加1,即逐位变反,在最低位加1。
如两个带符号的二进制数分别为S1和S2,其真值表达式为
S1= +11001 S2= -01011
则S1和S2的补码表示形式为
[S1]补= 011001 [S2]补= 110101
根据上述补码形成规则,一个n位的整数S (包括一位符号位)的补码一般表达式为
![]() (1.3.5)
(1.3.5)
同样,对于定点小数,补码一般表达式可写成
![]() (1.3.6)
(1.3.6)
由补码的一般表达式可以看出:
(1 )正数S的补码[S]补、反码[S]反和原码[S]原是相同的
(2 )对于负数,补码[S]补的符号位为1,其数值部分为反码的数值末位加1。
(3 )在补码表示法中,0的表示形式是唯一的。即
[+0]补= 0.00…0
[-0]补= 0.00…0
1. 3. 5 机器数的运算
前面介绍了带符号数的三种表示法,由于形成规则不同,加、减运算的规律也不相同。下面分别加以介绍。
一、原码运算
原码中的符号位仅用来表示数的正、负,不参加运算。进行运算的只是数值部分。原码运算时,应首先比较两个数的符号,若两数的符号相同,则可将两个数的数值相加,最后给结果附上相应的符号;若两数的符号不同,则需比较两数的数值大小,然后将数值较大的数减去数值较小的数,并将数值较大的数的符号作为最后结果的符号。下面举例说明。
例1.3.1 已知S1= 0.1001,S2= -0.0101,求[S2+S1 ]原和[S2-S1]原。
解: [S2+S1]原= [ (-0.0101 )+ (0.1001 )]原
由于S1和S2的符号不同,并且的S1绝对值大于S2的绝对值,因此要进行S1减S2的运算,其结果为正。
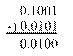
运算结果为原码,即
[S2+S1]原= 0.0100
故其真值为
S2+S1= 0.0100
又 [S2-S1]原= [ (-0.0101 )- (0.1001 )]原
由于S1和S2的符号相同,因此,实际上要进行Sl加S2的运算,其结果为负。
![]()
运算结果为原码,即
[S2-S1]原= 1.1101
故其真值为
S2-S1 = -0.1101
二、反码运算
由反码的定义可以得到反码加、减运算规则如下:
[S2+S1]反= [S2]反+[S1]反
[S2-S1]反= [S2]反+[-S1]反
反码的加、减运算规则表明:两数和的反码等于两数的反码之和,而两数差的反码也可以用加法来实现。运算时,符号位和数值位一样参加运算,如果符号位产生进位,则需将此进位加到和数的最低位,称之为“循环进位”。运算结果的符号位为0时,说明是正数的反码,与原码相同;运算结果的符号位为1时,说明是负数的反码,应再对运算结果求反码,才得到原码。下面举例说明。
例1.3.2 已知S1= 0.1001,S2= -0.0101,求[S2+S1]反和[S2-S1]反。
解: [S2+S1]反= [S2]反+ [S1]反= 1.1010+0.1001
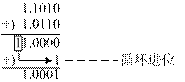
由于符号位产生了进位,因此要进行“循环进位”,即
[S2+S1]反= 0.0100
由于其符号位为0,则其真值为S2+S1= 0.0100
又 [S2-S1]反= [S2]反+ [-S1]反= 1.1010+1.0110
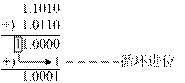
由于符号位产生了进位,因此要进行“循环进位”,即
[S2-S1]反= 1.0001
由于其符号位为1,则其真值为S2-S1= -0.1110
三、补码运算
补码运算同反码运算一样,两数差的补码可以用两数补码的加法来实现。补码加、减运算规则是:
[S2+S1]补= [S2]补+[S1]补
[S2-S1]补= [S2]补+[-S1]补
运算时,符号位和数值位一样参加运算,如果符号位产生了进位,则此进位可“略去”。运算结果符号位为0时,说明是正数的补码,与原码相同。运算结果符号位为l,说明是负数的补码,应对结果再求补码才得原码。
下面举例说明。
例1.3.3 已知S1= 0.1001,S2= -0.0101,求[S2+S1]补和[S2-S1]补。
解: [S2+S1]补= [S2]补+[S1]补= 1.1011+0.1001
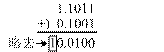
由于符号位产生了进位,因此,要将此进位略去,即
[S2+S1]补= 0.0100
运算结果的符号位为0,说明是正数的补码,补码与原码相同。
由于其符号位为0,则其真值为
S2+S1= 0.0100
又 [S2-S1]补= [S2]补+[-S1]补= 1.1011+1.0111

由于符号位产生了进位,因此,要将此进位略去,即
[S2-S1]补= 1.0010
运算结果的符号位为1,说明是负数的补码,应对补码求补后才能得到原码,即
[S2-S1]原= 1.1110
由于其符号位为1,则其真值为
S2-S1= -0.1110
从上述的讨论可以看出,原码、反码和补码各有优缺点。原码表示法简单方便,但原码减法必须做真正的减法,不能用加法来代替,因此实现原码运算所需的逻辑电路比较复杂。反码和补码的优点是只需用加法逻辑电路便可实现。并且用补码进行减法运算很方便,它只需进行一次算术相加。而用反码进行减法运算,若符号位产生进位就需进行两次算术相加。而且反码还有一个缺点,就是具有两个零值,这容易在计算过程中产生歧意。
