3.2.1简单逻辑门电路
一、与门
实现与运算逻辑功能的逻辑器件称为与门,每个与门有两个或两个以上的输入端和一个输出端,两输入端的与门的逻辑符号如图3.2.1(a)所示。

图3.2.1 与门、或门和非门的逻辑符号
在图3.2.1(a)中,![]() 、
、![]() 为输入端,
为输入端,![]() 为输出端,其输出和输入的电压取值关系如表3.2.1所示。假定高电平
为输出端,其输出和输入的电压取值关系如表3.2.1所示。假定高电平![]() 表示逻辑值1,低电平
表示逻辑值1,低电平![]() 表示逻辑值0,则这样的一个二值逻辑问题,输出和输入之间的逻辑关系如真值表3.2.2所示,输出
表示逻辑值0,则这样的一个二值逻辑问题,输出和输入之间的逻辑关系如真值表3.2.2所示,输出![]() 和输入
和输入![]() 、
、![]() 之间的逻辑关系表达式为:
之间的逻辑关系表达式为:
![]() (3.2.1)
(3.2.1)
|
表3.2.1 与门输出、输入的电压关系 |
||
|
输入 |
输出 |
|
|
|
|
|
|
VL |
VL |
VL |
|
VL |
VH |
VL |
|
VH |
VL |
VL |
|
VH |
VH |
VH |
|
表3.2.2 两输入端与门真值表 |
||
|
输入 |
输出 |
|
|
|
|
|
|
0 |
0 |
0 |
|
0 |
1 |
0 |
|
1 |
0 |
0 |
|
1 |
1 |
1 |
二、或门
实现或运算逻辑功能的逻辑器件称为或门。每个或门有两个或两个以上的输入端和一个输出端,两输入端或门的逻辑符号如图3.2.1(b)所示。图中![]() 、
、![]() 为输入端,
为输入端,![]() 为输出端,其输出和输入之间的电压取值关系如表3.2.3所示。同样假定高电平
为输出端,其输出和输入之间的电压取值关系如表3.2.3所示。同样假定高电平![]() 用逻辑值1表示,低电平
用逻辑值1表示,低电平![]() 用逻辑值0表示,或门的真值表如表3.2.4所示。或门输出和输入之间的逻辑关系表达式为:
用逻辑值0表示,或门的真值表如表3.2.4所示。或门输出和输入之间的逻辑关系表达式为:
![]() (3.2. 2)
(3.2. 2)
|
表3.2.3 或门输出、输入的电压关系 |
||
|
输入 |
输出 |
|
|
|
|
|
|
VL |
VL |
VL |
|
VL |
VH |
VH |
|
VH |
VL |
VH |
|
VH |
VH |
VH |
|
表3.2.4 两输入端与门真值表 |
||
|
输入 |
输出 |
|
|
|
|
|
|
0 |
0 |
0 |
|
0 |
1 |
1 |
|
1 |
0 |
1 |
|
1 |
1 |
1 |
三、非门
实现非逻辑运算功能的逻辑器件称为非门,非门也称作为反相器,每个非门有一个输入端和一个输出端,其逻辑符号如图3.2.1(c)所示。图中![]() 为输入端,
为输入端,![]() 为输出端,其输出和输入之间的电压取值关系如表3.2.5所示。同样假定高电平
为输出端,其输出和输入之间的电压取值关系如表3.2.5所示。同样假定高电平![]() 用逻辑值1表示,低电平
用逻辑值1表示,低电平![]() 用逻辑值0表示,则非门的真值表如表3.2.6所示。非门输出和输入之间的逻辑关系表达式为:
用逻辑值0表示,则非门的真值表如表3.2.6所示。非门输出和输入之间的逻辑关系表达式为:
![]() (3.2.3)
(3.2.3)
|
表3.2.5 或门输出、输入的电压关系 |
|
|
输入 |
输出 |
|
|
|
|
VL |
VH |
|
VH |
VL |
|
表3.2.6 或门输出、输入的电压关系 |
|
|
输入 |
输出 |
|
|
|
|
0 |
1 |
|
1 |
0 |
在表3.2.1、表3.2.3和表3.2.5中,高电平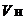 用1表示,低电平
用1表示,低电平 用0表示,则得到真值表3.2.2、表3.2.4和表3.2.6。输出和输入之间的电压关系转化成输出和输入之间的二值逻辑关系。那么,在实际的逻辑器件中,“高电平”的电压值是多高,“低电平”的电压值又是多低呢?对于不同类型的逻辑门电路,“高电平”和“低电平”的电压值各不相同。常见的双极型门电路中,(1)TTL门电路,“高电平”的典型值为
用0表示,则得到真值表3.2.2、表3.2.4和表3.2.6。输出和输入之间的电压关系转化成输出和输入之间的二值逻辑关系。那么,在实际的逻辑器件中,“高电平”的电压值是多高,“低电平”的电压值又是多低呢?对于不同类型的逻辑门电路,“高电平”和“低电平”的电压值各不相同。常见的双极型门电路中,(1)TTL门电路,“高电平”的典型值为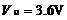 ,“低电平”的典型值为
,“低电平”的典型值为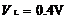 ;(2)ECL门电路,“高电平”的典型值为
;(2)ECL门电路,“高电平”的典型值为 ,“低电平”的典型值为
,“低电平”的典型值为 ;(3)I2L门电路,“高电平”的典型值为
;(3)I2L门电路,“高电平”的典型值为 ,“低电平”的典型值为
,“低电平”的典型值为 。MOS型逻辑门电路的高电平和低电平的电压值一般和电源电压有关,在电源电压为5V时,CMOS门电路高电平的
。MOS型逻辑门电路的高电平和低电平的电压值一般和电源电压有关,在电源电压为5V时,CMOS门电路高电平的 ,低电平电压为
,低电平电压为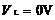 。可以看出,只有相同类型的门电路,其电平才相匹配,不同类型的门电路,其电平是不相匹配的,如ECL门电路的高电平电压值比TTL门电路和I2L门电路的低电平电压值还要低,因此,当某一类型的门电路的输出信号要作为另一类型门电路的输入信号时,必须在它们之间增加一种电压转换电路,否则将出现错误的输出。
。可以看出,只有相同类型的门电路,其电平才相匹配,不同类型的门电路,其电平是不相匹配的,如ECL门电路的高电平电压值比TTL门电路和I2L门电路的低电平电压值还要低,因此,当某一类型的门电路的输出信号要作为另一类型门电路的输入信号时,必须在它们之间增加一种电压转换电路,否则将出现错误的输出。
3.2.2复合逻辑门电路
从理论上讲,由与、或、非三种门电路可以实现各种逻辑功能,在实际的应用中发现不论是何种制造工艺的与、或、非门在性能上存在许多的不足,如带负载能力弱,抗干扰能力差等。而在实际中广泛使用的门在带负载能力、稳定性和可靠性等方面都有显著提高,最常用的复合逻辑门有“与非”门、“或非”门、“与或非”门和“异或”门等,其逻辑符号如图3.2.2所示:
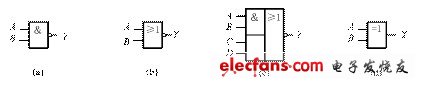
一、与非门
与运算后再进行非运算的复合运算称为与非运算,实现与非运算的逻辑电路称为与非门。与非门有两个或两个以上的输入端和一个输出端,两输入端与非门的逻辑符号如图3.2.2(a)所示。图中 、
、 为输入端,
为输入端,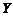 为输出端。假定高电平为
为输出端。假定高电平为 ,低电平为
,低电平为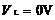 ,输出
,输出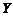 和输入
和输入 、
、 的电压取值关系如表3.2.7所示,高电平5V用逻辑值1表示,低电平0V用逻辑值0表示,电压取值关系转换为二值逻辑关系的真值表如表3.2.8所示。
的电压取值关系如表3.2.7所示,高电平5V用逻辑值1表示,低电平0V用逻辑值0表示,电压取值关系转换为二值逻辑关系的真值表如表3.2.8所示。
|
表3.2.7 与非门输出、输入的电压关系 |
||
|
输 入 |
输 出 |
|
|
|
|
|
|
0 V |
0 V |
5 V |
|
0 V |
5 V |
5 V |
|
5 V |
0 V |
5 V |
|
5 V |
5 V |
0 V |
|
表3.2.8 两输入端与非门真值表 |
||
|
输 入 |
输出 |
|
|
|
|
|
|
0 |
0 |
1 |
|
0 |
1 |
1 |
|
1 |
0 |
1 |
|
1 |
1 |
0 |
输出与输入之间的逻辑关系表达式为:
![]() (3.2.4)
(3.2.4)
使用与非门可实现任何逻辑功能的逻辑电路,因此,与非门是通用逻辑门的一种。
二、或非门
或运算后再进行非运算的复合运算称为或非运算,实现或非运算的逻辑电路称为或非门。或非门也是一种通用逻辑门。一个或非门有两个或两个以上的输入端和一个输出端,两输入端或非门的逻辑符号如图3.2.2(b)所示。图中 、
、 为输入端,
为输入端,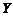 为输出端。假定高电平为
为输出端。假定高电平为 ,低电平为
,低电平为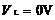 ,输出
,输出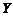 和输入
和输入 、
、 的电压取值关系如表3.2.9所示。其二值逻辑关系的真值表如表3.2.10所示。或非运算的逻辑表达式为
的电压取值关系如表3.2.9所示。其二值逻辑关系的真值表如表3.2.10所示。或非运算的逻辑表达式为
![]() (3.2.5)
(3.2.5)
|
表3.2.9 或非门输出输入的电压关系 |
||
|
输入 |
输出 |
|
|
|
|
|
|
0 V |
0 V |
+5 V |
|
0 V |
+5 V |
+5 V |
|
+5 V |
0 V |
+5 V |
|
+5 V |
+5 V |
0 V |
|
表3.2.10 两输入端或非门真值表 |
||
|
输入 |
输出 |
|
|
A |
B |
Y |
|
0 |
0 |
1 |
|
0 |
1 |
0 |
|
1 |
0 |
0 |
|
1 |
1 |
0 |
三、与或非门
与、或、非三种运算的复合运算称为与或非运算,实现与或非运算的逻辑电路称为与或非门。它也是一种通用逻辑门。图3.2.2(c)所示为与或非门的逻辑符号,高电平用逻辑值1表示;低电平用逻辑值0表示,与或非门电路输出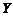 和输入
和输入 、
、 、
、 、
、 的逻辑性关系如表3.2.11所示,其逻辑表达式为:
的逻辑性关系如表3.2.11所示,其逻辑表达式为:
![]() (3.2.6)
(3.2.6)
|
表3.2.11 “与或非”门真值表 |
||||||||||
|
输入 |
输出 |
|
输入 |
输出 |
||||||
|
A |
B |
C |
D |
Y |
A |
B |
C |
D |
Y |
|
|
0 |
0 |
0 |
0 |
1 |
1 |
0 |
0 |
0 |
1 |
|
|
0 |
0 |
0 |
1 |
1 |
1 |
0 |
0 |
1 |
1 |
|
|
0 |
0 |
1 |
0 |
1 |
|
1 |
0 |
1 |
0 |
1 |
|
0 |
0 |
1 |
1 |
0 |
|
1 |
0 |
1 |
1 |
0 |
|
0 |
1 |
0 |
0 |
1 |
|
1 |
1 |
0 |
0 |
0 |
|
0 |
1 |
0 |
1 |
1 |
|
1 |
1 |
0 |
1 |
0 |
|
0 |
1 |
1 |
0 |
1 |
|
1 |
1 |
1 |
0 |
0 |
|
0 |
1 |
1 |
1 |
0 |
|
1 |
1 |
1 |
1 |
0 |
四、异或门
异或逻辑是指两个输入端取值不同时,输出为1,当两个输入端取值相同时,输出为0。实现异或逻辑运算的逻辑电路称为异或门。异或门有且仅有两个输入端,一个输出端。图3.2.2(d)所示为异或门的逻辑符号,图中,输出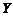 和输入
和输入 、
、 的逻辑关系如真值3.2.12所示,相应的逻辑表达式为:
的逻辑关系如真值3.2.12所示,相应的逻辑表达式为:
 (3.2.7)
(3.2.7)
|
表3.2.12 “异或”门真值表 |
||
|
输入 |
输出 |
|
|
|
|
|
|
0 |
0 |
0 |
|
0 |
1 |
1 |
|
1 |
0 |
1 |
|
1 |
1 |
0 |
|
表3.2.13 “同或”门真值表 |
||
|
输入 |
输出 |
|
|
|
|
|
|
0 |
0 |
1 |
|
0 |
1 |
0 |
|
1 |
0 |
0 |
|
1 |
1 |
1 |
异或运算之后再进行非运算,则称为同或运算,相应的真值表见表3.2.13,同或运算的逻辑表达式为:
![]() ⊙
⊙![]() (3.2.8)
(3.2.8)
3.2.3正负逻辑问题
上述讨论中,电子电路中的高电平和低电平分别表示二值逻辑的1和0 两种逻辑状态,高电平![]() 和低电平
和低电平![]() 是两个不同的可以截然区别开来的电压范围。例如,在图3.2.3中,2.4~5V范围内电压,都称作高电平,对应于
是两个不同的可以截然区别开来的电压范围。例如,在图3.2.3中,2.4~5V范围内电压,都称作高电平,对应于![]() ;而在0~0.8V范围内的电压,都称作低电平,对应于
;而在0~0.8V范围内的电压,都称作低电平,对应于![]() 。
。

正负逻辑的概念反映高电平 和低电平
和低电平 所代表的意义,规定如下:
所代表的意义,规定如下:
正逻辑关系:高电平 用逻辑值1表示,低电平
用逻辑值1表示,低电平 用逻辑值0表示。
用逻辑值0表示。
负逻辑关系:高电平 用逻辑值0表示,低电平
用逻辑值0表示,低电平 用逻辑值1表示。
用逻辑值1表示。
正逻辑和负逻辑之间有一定的转换关系,如表3.2.1与门的输出、输入电压关系用负逻辑表示,相应真值表变成表3.2.14所示:
|
表3.2.14 与门负逻辑表示 |
||
|
输入 |
输出 |
|
|
|
|
|
|
1 |
1 |
1 |
|
1 |
0 |
1 |
|
0 |
1 |
1 |
|
0 |
0 |
0 |
|
表3.2.15 或门负逻辑表示 |
||
|
输入 |
输出 |
|
|
|
|
|
|
1 |
1 |
1 |
|
1 |
0 |
0 |
|
0 |
1 |
0 |
|
0 |
0 |
0 |
与表3.2.4两输入端或门真值表完全一致。同样表3.2.3或门的输出、输入电压关系,用负逻辑表示,相应的真值表变成表3.2.15所示,与表3.2.2两输入端与门真值表完全一致。可以看出,正逻辑中的与门是负逻辑中的或门,正逻辑中的或门是负逻辑中的与门。本书若无特别说明,一律采用正逻辑关系。实际上,正、负逻辑之间的变换可以利用反演律(或称摩根定律)来证明。例如,有一个两输入端正与门,输入为 、
、 ,输出为
,输出为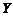 ,则有
,则有
![]() (3.2.9)
(3.2.9)
对(3.2.9)式两边同时取非,由反演律,可得
![]() (3.2.10)
(3.2.10)
在(3.2.10)式中,令
![]() (3.2.11)
(3.2.11)
可得:![]() (3.2.12)
(3.2.12)
显然,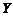 、
、 、
、 的值取1时,而
的值取1时,而 、
、 、
、 的值为0,即正逻辑变为负逻辑,由(3.2.9)式表示的正逻辑关系与门变成由(3.2.12)式表示的负逻辑关系或门。
的值为0,即正逻辑变为负逻辑,由(3.2.9)式表示的正逻辑关系与门变成由(3.2.12)式表示的负逻辑关系或门。
图3.2.4给出了几种常用的正负逻辑的等效变换。

由图3.2.4从正逻辑符号变换成负逻辑符号时,在门电路符号输入端和输出端同时加小圆圈,表示反相。如果该处原来有小圆圈,按非—非相消的原则,可把小圆圈删掉。同时,将与门符号变为或门符号,或门符号变为与门符号,就得出负逻辑符号。
应当指出,在负逻辑符号中, 、
、 、
、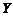 取正逻辑值,
取正逻辑值, 、
、 、
、 才是负逻辑值,在正逻辑中小圆圈表示反相,也可表示负逻辑。
才是负逻辑值,在正逻辑中小圆圈表示反相,也可表示负逻辑。
利用负逻辑的表示方法,通过符号置换,对逻辑电路的分析与综合带来方便。下面举例说明。
例3.2.1在图3.2.5(a)所示三级与非门组成的逻辑电路中,试求出其逻辑表达式。

解 若直接由逻辑图写出逻辑表达式,则:
![]()
然后,需要多次应用反演律才可将表达式化成与-或表达式,且演算过程复杂。
如果将输出级和奇数级上的与非门进行置换,正与非门置换为负或非门,如图3.2.5(b)所示。在图3.2.5(b)中,第Ⅰ级输入端的小圆圈可与第Ⅱ级输出端的小圆圈相互抵消,即非—非相消,第Ⅱ级就变成了与门。第Ⅲ级输入端的小圆圈可移入变量,如原输入量为 ,小圆圈删掉后。输入量变为
,小圆圈删掉后。输入量变为 ,原输入量
,原输入量 、
、 小圆圈删掉后,输入量变为
小圆圈删掉后,输入量变为 、
、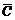 ,如图3.2.6所示。
,如图3.2.6所示。

这样置换后,很容易写出输出表达式:
![]() (3.2.13)
(3.2.13)
