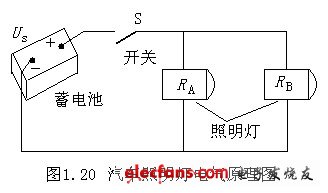
蓄电池是一种常见的电源，它多用于汽车、电力机车、应急灯等，图1.20是汽车照明灯的电气原理图。其中，RA、RB是一对汽车照明灯；S是开关；US是12V的蓄电池。
常见的电源还有发电机、干电池和各种信号源。凡是向电路提供能量或信号的设备称为电源。电源有两种类型，其一为电压源，其二为电流源。电压源的电压不随其外电路而变化，电流源的电流不随其外电路而变化，因此，电压源和电流源总称为独立电源，简称独立源。
1.4.1 电压源
1．理想电压源
理想电压源简称为电压源，是一个二端元件，它有两个基本特点：
（1）无论它的外电路如何变化，它两端的输出电压为恒定值US，或为一定时间的函数us（t）。
（2）通过电压源的电流虽是任意的，但仅由它本身是不能决定的，还取决于与之相连接的外部电路，有时甚至完全取决于外电路。
电压源在电路图中的符号如图1．21（a）所示，其电压用us表示。若us（t）的大小和方向都不随时间变化称为直流电压源，其电压用US表示。图1．21（b）是直流电压源的另一种符号，且长线表示参考正极性，短线表示参考负极性。
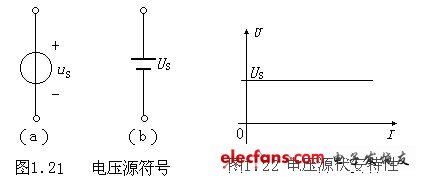
直流电压源的伏安特性如图1．22所示，它是一条以I为横坐标且平行于I轴的直线，表明其电流由外电路决定，不论电流为何值，直流电压源端电压总为US。
us（t）=0的电压源是电压保持为零、电流由其外电路决定的二端元件，因此，us（t）=0的电压源可相当于R=0的电阻元件。在实际应用中，可以用一条短路导线来代替us（t）=0的电压源。
同样，在实际应用中，不能将us（t）不相等的电压源并联，也不能将us（t）≠0的电压源短路。
2．实际电压源
电压源这种理想二端元件实际上是不存在的。实际的电压源，其端电压都是随着电流的变化而变化的。例如，当电池接通负载后，其电压就会降低，这是因为电池内部存在电阻的缘故。由此可见，实际的直流电压源可用数值等于US的理想电压源和一个内阻Ri相串联的模型来表示，如图1．23（a）所示。
于是，实际直流电压源的端电压为：
U=US-UR=US-IRi （1．16）
式中，US的参考方向与U的参考方向一致，取正号；UR的参考方向与U的参考方向相反，取负号。式1．16所描述的U与I的关系，即实际直流电压源的伏安特性，如图1．23（b）所示。
例1．4 图1．24所示电路，直流电压源的电压US=10V。求：
（1）R=∞时的电压U，电流I；
（2）R=10Ω时的电压U，电流I；
（3）R→0Ω时的电压U，电流I。
解：
（1）R=∞时即外电路开路，US为理想电压源，故
U=US=10V
则 
（2）R=10Ω时
U=US=10V
则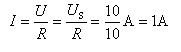 
（3）R→0Ω时
U=US=10V
则 
1.4.2 电流源
1．理想电流源
理想电流源简称为电流源，是一个二端元件，它有两个基本特点：
（1）无论它的外电路如何变化，它的输出电流为恒定值IS，或为一定时间的函数iS（t）。
（2）电流源两端的电压虽是任意的，但仅由它本身是不能决定的，还取决于与之相连接的外部电路，有时甚至完全取决于外电路。
电流源在电路图中的符号如图1．25所示，其中电流源的电流用is表示，电流源的端电压为uS。若is（t）的大小和方向都不随时间变化称为直流电流源，其电流用IS表示。
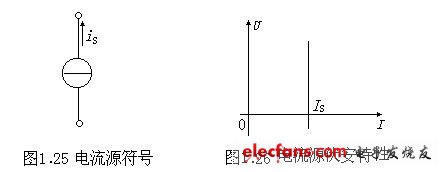
直流电流源的伏安特性如图1．26所示，它是一条以I为横坐标且垂直于I轴的直线，表明其端电压由外电路决定，不论其端电压为何值，直流电流源输出电流总为IS。
is（t）=0的电流源是电流保持为零、电压由其外电路决定的二端元件，因此，is（t）=0的电流源就相当于R=∞的电阻元件。在实际应用中，可以用一条开路导线来代替is（t）=0的电流源。
同样，在实际应用中，不能将is（t）不相等的电流源串联，也不能将is（t）≠0的电流源开路。
2．实际电流源
电流源这种理性二端元件实际上是不存在的。实际的电流源，其输出的电流是随着端电压的变化而变化的。例如，光电池在一定照度的光线照射下，被光激发产生的电流，并不能全部外流，其中的一部分将在光电池内部流动。由此可见，实际的直流电流源可用数值等于IS的理想电流源和一个内阻Ri‘相并联的模型来表示，如图1．27（a）所示。
于是，实际直流电流源的输出电流为：
式中，IS为实际直流电流源产生的恒定电流；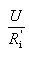
为其内部分流电流。式1．17所描述的U与I的关系，即实际直流电流源的伏安特性，如图1．27（b）所示。
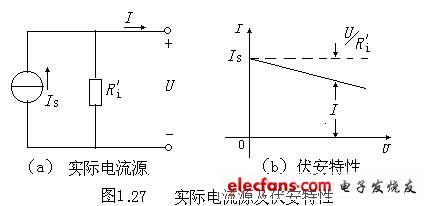
例1．5 图1．28所示电路，直流电流源的电流IS=1A。求：
（1）R→∞时的电流I，电压U；
（2）R=10Ω时的电流I，电压U；
（3）R=0Ω时的电流I，电压U。
解：
（1）R→∞时即外电路开路，IS为理想电流源，故
I=IS=1A
则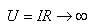 
（2）R=10Ω时
I=IS=1A
则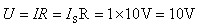 
（3）R=0Ω时
I=IS=1A
则 
1.4.3 电源的等效变换
任何一个实际电源本身都具有内阻，因而实际电源的电路模型往往由理想电源元件与其内阻组合而成。理想电源元件有电压源和电流源，因此，实际电源的电路模型也相应的有电压源模型和电流源模型，如图1．29所示。
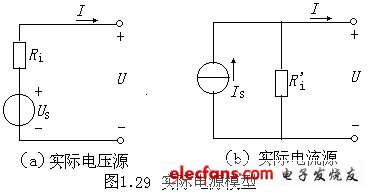
在图1．29（a）电路中，由式（1．16）可知：
U=US-IRi
式中，US为电压源的电压。
在图1．29（b）电路中，由式（1．17）可知：
整理后得：
U=ISRi‘-IRi‘
由此可见，实际电压源和实际电流源若要等效互换，其伏安特性方程必相同，则其电路参数必须满足条件：
Ri= Ri‘；US=ISRi‘ （1．18）
即当实际电压源等效变换成实际电流源时，电流源的电流等于电压源的电压与其内阻的比值，电流源的内阻等于电压源的内阻；当实际电流源等效变换成实际电压源时，电压源的电压等于电流源的电流与其内阻的乘积，电压源的内阻等于电流源的内阻。
在进行等效互换时，必须重视电压源的电压极性与电流源的电流方向之间的关系，即两者的参考方向要求一致，也就是说电压源的正极对应着电流源电流的流出端。
实际电源的两种模型的等效互换只能保证其外部电路的电压、电流和功率相同，对其内部电路，并无等效而言。通俗地讲，当电路中某一部分用其等效电路替代后，未被替代部分的电压、电流应保持不变。
应用电源等效互换分析电路时还应注意这样几点：
（1）电源等效互换是电路等效变换的一种方法。这种等效是对电源输出电流I、端电压U的等效。
（2）有内阻Ri的实际电源，它的电压源模型与电流源模型之间可以互换等效；理想的电压源与理想的电流源之间不便互换。
（3）电源等效互换的方法可以推广运用，如果理想电压源与外接电阻串联，可把外接电阻看其作内阻，则可互换为电流源形式；如果理想电流源与外接电阻并联，可把外接电阻看作其内阻，则可互换为电压源形式。
例1．6 已知Us1=4V，Is2=2A，R2=1.2Ω，试等效化简图1．30所示电路。
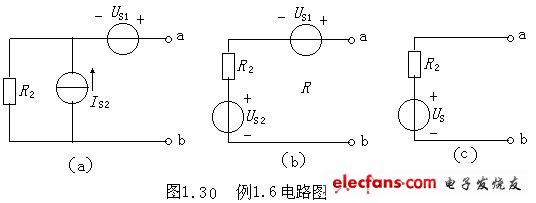
解：在图1．30（a）中，把电流源IS2与电阻R2的并联变换为电压源US2与电阻R2的串联，电路变换如图1．30（b），其中
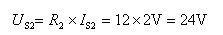
在图1．30（b）中，将电压源US2与电压源US1的串联变换为电压源US，电路变换如图1．30（c），其中
US=US2+US1=（24+4）V=28V
例1．7 电路如图1．31所示，已知Us1=10V，Is1=15A，Is2=5A，R=30Ω，R2=20Ω，求电流I。
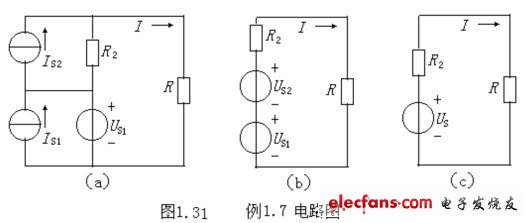
解：在图1．31（a）中，电压源US1与电流源IS1并联可等效为该电压源US1；电流源IS2与电阻R2的并联可等效变换为电压源US2与电阻R2的串联，电路变换如图1．31（b），其中
US2=IS2R2=5×20V=100V
在图1．31（b）中，电压源US1与电压源US2的串联可等效变换电压源U，电路变换如图1．31（c），其中
US=US2+US1=（100+10）V=110V
在图1．31（c）中，根据欧姆定律可知：
