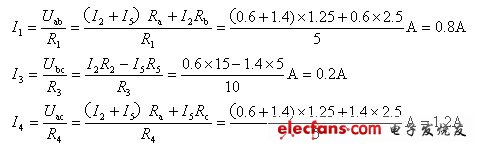具有两个端钮的部分电路,就称为二端网络,如图2.1所示。
如果电路结构、元件参数完全不同的两个二端网络具有相同的电压、电流关系即相同的伏安关系时,则这两个二端网络称为等效网络。等效网络在电路中可以相互代换。
内部没有独立源的二端网络,称为无源二端网络,它可用一个电阻元件与之等效。这个电阻元件的电阻值称为该网络的等效电阻或输入电阻,也称为总电阻,用Ri表示。
2.1.1电阻的串联
案例2.1 电压表的表头所能测量的最大电压就是其量程,通常它都较小。在测量时,通过表头的电流是不能超过其量程的,否则将损坏电流表。而实际用于测量电压的多量程的电压表(例如,C30-V型磁电系电压表)是由表头与电阻串联的电路组成,如图2.2所示。其中,Rg为表头的内阻,Ig为流过表头的电流,Ug为表头两端的电压,R1、R2、R3、R4为电压表各档的分压电阻。对应一个电阻档位,电压表有一个量程.

以上就是利用了串联电阻的“分压”作用来扩大电压表的量程。
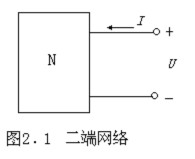
各电阻元件顺次连接起来,所构成的二端网络称为电阻的串联网络,如图2.3(a)所示。
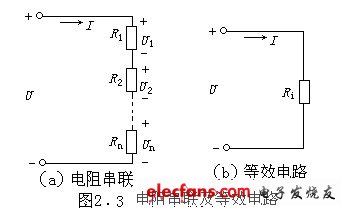
在图2.3(a)中,根据KCL定理可知,串联的各个电阻的电流相等,均等于I,则由KVL定理可得:
U=U1+U2+…+Un,
即:电阻的串联网络的端口电压等于各电阻电压之和。
又由欧姆定律可得:
U1=R1I,U2=R2I,…,Un=RnI,
于是,U=R1I+R2I+…+RnI=(R1+R2+…+Rn)I
图2.3(b)是图2.3(a)的等效网络,根据等效的概念,在图2.3(b)中有:U=RiI
因此,Ri=R1+R2+…+Rn,
即:电阻的串联网络的等效电阻等于各电阻之和。
串联电阻的等效电阻比每个电阻都大,在端口电压一定时,串联电阻越多,电流则越小,因此串联电阻有“限流”作用。
串联电阻的电流相等,则各电阻的电压之比等于它们的电阻之比,即:
U1:U2:…:Un=R1:R2:…:Rn
各电阻的电压与端电压U的关系为:

即:电阻的串联网络的每个电阻的电压与端口电压的比等于该电阻与等效电阻的比,这个比值称为“分压比”。在端口电压一定时,适当选择串联电阻,可使每个电阻得到所需要的电压,因此串联电阻有“分压”作用。
同理,串联的每个电阻的功率也与它们的电阻成正比,即:
P1:P2:…:Pn=R1:R2:…:Rn
例2.1 如图2.2所示的C30-V型磁电系电压表,其表头的内阻Rg=29.28Ω,各档分压电阻分别为R1=970.72Ω,R2=1.5KΩ,R3=2.5KΩ,R4=5KΩ;这个电压表的最大量程为30V。试计算表头所允许通过的最大电流值Igm、表头所能测量的最大电压值Ugm以及扩展后的各量程的电压值U1、U2、U3、U4。
解:当开关在“4”档时,电压表的总电阻Ri为:
Ri=Rg+R1+R2+R3+R4=(29.28+970.72+1500+2500+5000)Ω=10000Ω=10KΩ
通过表头的最大电流值Igm为:

当开关在“1”档时,电压表的量程U1为:
U1=(Rg+R1)I=(29.28+970.72)×3mV=3V
当开关在“2”档时,电压表的量程U2为:
U2=(Rg+R1+R2)I=(29.28+970.72+1500)×3mV=7.5V
当开关在“3”档时,电压表的量程U3为:
U3=(Rg+R1+R2+R3)I=(29.28+970.72+1500+2500)×3mV=15V
表头所能测量的最大电压Ugm为:
Ugm= RgI=29.28×3mV=87.84 mV
由此可见,直接利用表头测量电压时,它只能测量87.84 mV以下的电压,而串联了分压电阻R1、R2、R3、R4后,它就有3V、7.5、15V、30V四个量程,实现了电压表的量程扩展。
2.1.2电阻的并联
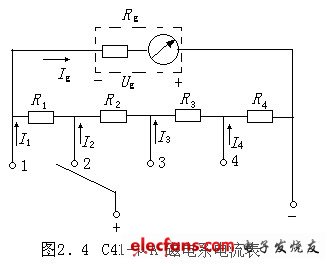
案例2.2 实际用于测量电流的多量程的电流表(例如,C41-μA磁电系电流表)是由表头与电阻串、并联的电路组成,如图2.4所示。其中,Rg为表头的内阻,Ig为流过表头的电流,Ug为表头两端的电压,R1、R2、R3、R4为电流表各档的分流电阻。对应一个电阻档位,电流表有一个量程。
以上就是利用了并联电阻的“分流”作用来扩大电流表的量程。
各电阻元件的两端钮分别连接起来所构成的二端网络称为电阻的并联网络,如图2.5(a)所示。
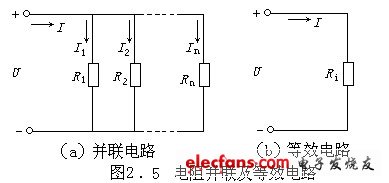
在图2.5(a)中,根据KVL定理可知,并联的各个电阻的电压相等,均等于U,则由KCL定理可得:
I=I1+I2+…+In,
即:电阻的并联网络的端电流等于各电阻电流之和。
又由欧姆定律可得:
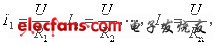
于是,
图2.5(b)是图2.5(a)的等效网络,根据等效的概念,在图2.5(b)中有: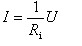
因此,
即:电阻的并联网络的等效电阻的倒数等于各电阻倒数之和或电阻的并联网络的等效电导等于各电阻的电导之和。且并联电阻的等效电阻比每个电阻都小。
并联电阻的压相等,则各电阻的电流与它们的电导成正比,与它们的电阻成反比,即:

各电阻的电流与端电流I的关系为:

即:电阻的并联网络的每个电阻的电流与端电流的比等于该电导与等效电导的比,这个比值称为“分流比”。在端电流一定时,适当选择并联电阻,可使每个电阻得到所需要的电流,因此并联电阻有“分流”作用。
同理,并联的每个电阻的功率也与它们的电导成正比,与它们的电阻成反比。即:

若只有R1、R2两个电阻并联,如图2.6所示,

由

可得等效电阻Ri为:
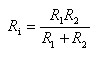
两个电阻的电流分别为:

如果R1=R2=R,则有:

例2.2 如图2.4所示的C41-μA型磁电系电流表,其表头内阻Rg=1.92KΩ,各分流电阻分别为R1=1.6KΩ,R2=960Ω,R3=320Ω,R4=320Ω;表头所允许通过的最大电流为62.5μA,试求表头所能测量的最大电压Ugm以及扩展后的电流表各量程的电流值I1、I2、I3、I4。
解:表头所允许通过的最大电流为62.5μA。当开关在“1”档时,R1、R2、R3、R4是串联的,而Rg与它们相并联,根据分流公式可得
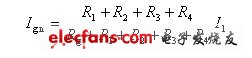
则有
当开关在“2”档时,Rg、R1是串联的,而R2、R3、R4与它们相并联,根据分流公式可得

则有
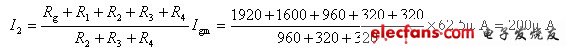
同理,当开关在“3”档时,Rg、R1、R2是串联的,而R3、R4串联后与它们相并联,根据分流公式可得

则有
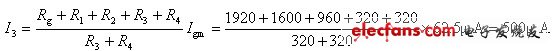
当开关在“4”档时,Rg、R1、R2、R3是串联的,而R4与它们相并联,根据分流公式可得

则有

由此可见,直接利用该表头测量电流,它只能测量62.5μA以下的电流,而并联了分流电阻R1、R2、R3、R4后,作为电流表,它就有100μA、200μA、500μA、1000μA四个量程,实现了电流表量程的扩展。
由串联和并联电阻组合而成的二端电阻网络称为电阻的混联网络,分析混联电阻网络的一般步骤如下:
(1)计算各串联电阻、并联电阻的等效电阻,再计算总的等效电阻。
(2)由端口激励计算出端口响应。
(3)根据串联电阻的分压关系、并联电阻的分流关系逐步计算各部分电压、电流。
例2.3图2.7所示的是一个常用的利用滑线变阻器组成的简单分压器电路。电阻分压器的固定端a、b接到直流电压源上。固定端b与活动端c接到负载上。利用分压器上滑动触头c的滑动可在负载电阻上输出0~U的可变电压。已知直流理想电压源电压US=9V,负载电阻RL=800Ω,滑线变阻器的总电阻R=1000Ω,滑动触头c的位置使R1=200Ω,R2=800Ω。
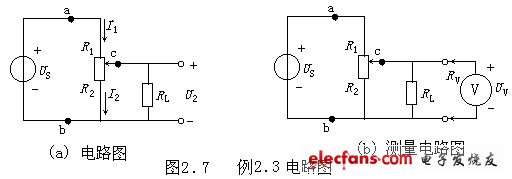
(1)求输出电压U2及滑线变阻器两段电阻中的电流I1、I2;
(2)若用内阻为RV1=1200Ω的电压表去测量此电压,求电压表的读数;
(3)若用内阻为RV2=3600Ω的电压表再测量此电压,求这时电压表的读数。
解:
(1)图2.7(a)中,电阻R2与RL并联后再与R1串联。

(2)图2.7(b)中,电阻R2、RL与电压表内阻RV1并联后再与R1串联。
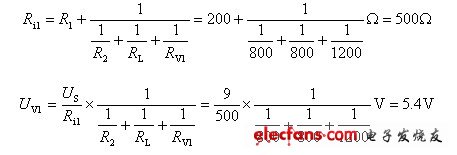
(3)图2.7(b)中,电阻R2、RL与电压表内阻RV2并联后再与R1串联。
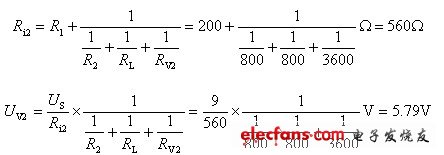
由此可见,由于实际电压表都有一定的内阻,将电压表并联在电路中测量电压时,对被测试电路都有一定的影响。电压表内阻越大,对测试电路的影响越小。理想电压表的内阻为无穷大,对测试电路才无影响,但实际中并不存在。
2.1.3电阻星形联接与三角形联接的等效变换
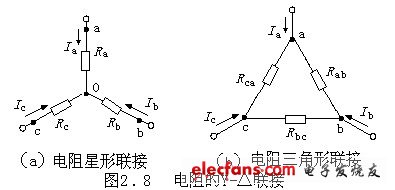
三个电阻的一端连接在一起构成一个节点O,另一端分别为网络的三个端钮a、b、c,它们分别与外电路相连,这种三端网络叫电阻的星形联接,又叫电阻的Y联接。如图2.8(a)所示。
三个电阻串联起来构成一个回路,而三个连接点为网络的三个端钮a、b、c,它们分别与外电路相连,这种三端网络叫电阻的三角形联接,又叫电阻的△联接。如图2.8(b)所示。
在图示参考方向下,由KCL、KVL定理可知:
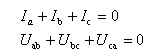
可以证明,将△联接的电阻等效变换为Y联接的电阻,已知电阻Rab、Rbc、Rca,则等效的电阻Ra、Rb、Rc为:

将Y联接的电阻等效变换为△联接的电阻,已知Ra、Rb、Rc电阻,则等效的电阻Rab、Rbc、Rca为:

三个相等电阻的Y、△联接方式叫做Y、△的对称联接。如果对称Y联接的电阻为RY,则对称△联接的等效电阻R△为:
例2.4图2.9(a)所示电路中,已知IS=29A,R1= R3= R6= 3Ω,R2=13.5Ω, R4=1Ω,R5=6Ω,试求电阻R1、R2、R3的电流I1、I2、I3及电阻R5的电压U5。
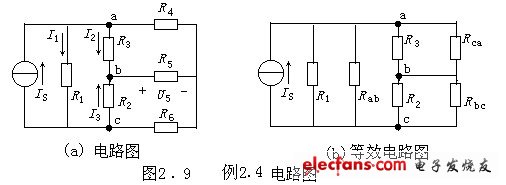
解:利用公式(2.2),将Y联接的电阻R4、R5、R6等效变换为△联接的电阻Rab、Rbc、Rca,如图2.9(b)所示,则:

图b是电阻的混联网络,并联的R3、Rca的等效电阻R3-ca为:
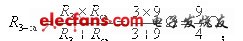
并联的R2、Rbc的等效电阻R2-bc为:
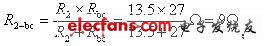
串联的R3-ca、R2-bc的等效电阻R‘为:

则电路中电阻R1的电流I1为:

电阻R2、R3的电流I2、I3分别为:
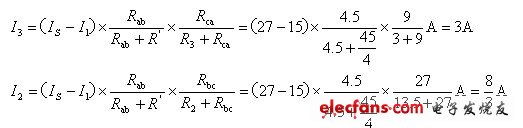
电阻R5的电压U5为:

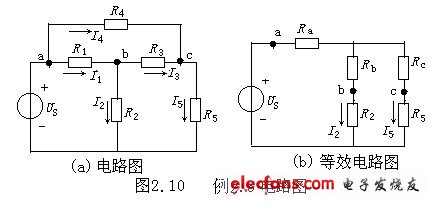
例2.5 图2.10(a)所示电路,US=13V,R1=R4=R5=5Ω,R2=15Ω,R3=10Ω,(1)试求它的等效电阻R; (2)试求各电阻的电流。
解:
(1)利用公式(2.1),将△联接的电阻R1、R3、R4等效变换为Y联接的电阻Ra、Rb、Rc,如图2.10(b)所示,则:
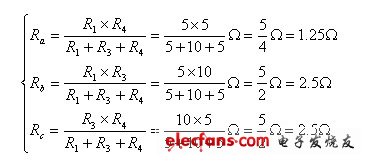
图2.10(b)是电阻的混联网络,串联的R2、Rb的等效电阻R2b为:
R2b=R2+Rb=(15+2.5)Ω=17.5Ω,
串联的R5、Rc的等效电阻R5c为:
R5c=R5+Rc=(5+2.5)Ω=7.5Ω
电路的等效电阻R为:

(2)电路中电阻R2、R5的电流I2、I5为:

为求得电阻R1、R3、R4的电流I1、I3、I4,可从图2-1-10(b)分别求得电压Uab、Ubc、Uac,再回到图2.10(a)求解,则: