第4节 总结与习题

本章小结

本章主要介绍了三个方面的内容。

1．无源网络的等效变换

（1）电阻串并联等效变换

1）电阻的串联及其分压

R_i=R₁+R₂+…+R_n，

U₁：U₂：…：U_n=R₁：R₂：…：R_n

2）电阻的并联及其分流

3）两个电阻的并联及其分流

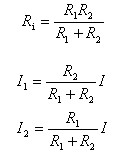
（2）电阻星形联接与三角形联接的等效变换

1）Y→△变换公式

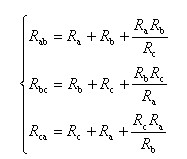
2）△→Y变换公式

2．电路基本定理

（1）叠加定理

叠加定理适用于线性电路的电压、电流的计算。即各支路的电压、电流可看作由各个电源单独作用（其它电压源用短路代替，电流源用开路代替）时在该支路所产生的电压、电流的代数和。

叠加定理反映了线性电路的基本性质，它也是推导某些定理和电路分析方法的依据。

（2）戴维宁定理

戴维宁定理是等效电路概念的具体运用。它指出：任何一个线性有源电阻性二端网络，对外电路来说，可以用一个电压源与一个电阻串联的支路等效代替。电压源的电压等于该网络的开路电压，电阻等于该网络中所有电压源短路、电流源开路时的等效电阻。

戴维宁定理特别适用于求解线性有源电阻性二端网络的某支路电流或电压。解题过程可分为如下三个步骤进行。

1）求开路电压；

2）求等效电阻；

3）作出戴维南等效电路，计算所求支路的电流或电压。

（3）诺顿定理

诺顿定理也是等效电路概念的具体运用，同时它也是戴维宁定理的推论。 

习题

2．1电阻R₁、R₂串联，已知总电压U=10V，总电阻R₁+R₂=100Ω，测出R₁上电压为2V，求R₁和R₂的阻值。

2．2两电阻R₁、R₂并联，已知R₁=10Ω，R₂=30Ω，总电流I=12A，试求等效电阻及流过每个电阻的电流。

2．3在图2．25所示电路中，已知电阻R₁=R₂=R₃=R₄=9Ω，R₅=3Ω，电压U_S=21V，求电压U₅。

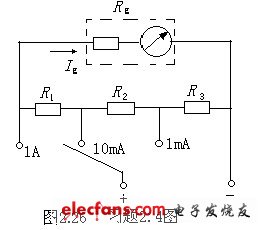
2．4在图2．26所示电路中，利用一只内阻R_g=1600Ω，I_g=100μA的表头，如要求扩大量程为1mA、10mA、1A三档，求电阻R₁、R₂、R₃。

2．5在图2．27所示电路中，已知电阻R₁=600Ω，R₂=R₃=300Ω，R₄=R₅=200Ω，R₆=400Ω，R₇=800Ω，电压U_S=34V，求电流I₇。

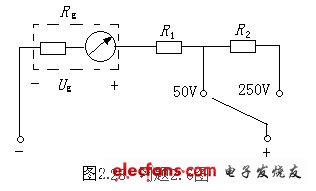
2．6在图2．28所示电路中，一个电压表量程为1V，内阻为1KΩ，若欲将电压表量程扩大为50V及250V，所须串联的电阻的阻值为多少。

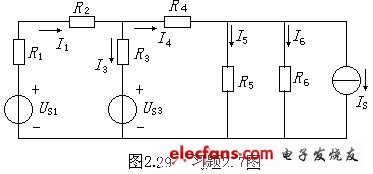
2．7在图2．29所示电路中，已知电阻R₁=2Ω，R₂=3Ω，R₃=0.1Ω，R₄=5Ω，R₅=10Ω，R₆=4Ω，电压U_S1=20V，U_S3=10V，电流I_S=40A，求电路中各支路电流。

2．8在图2．３0所示电路中，已知电阻R₁=5Ω，R₂=4Ω，R₃=R₅=20Ω，R₄=2Ω，R₆=10Ω，电压U_S1=15V，U_S2=10V，U_S6=4V，求电路中各支路电流。

2．9在图2．３1所示电路中，已知电阻R₁=R₃=R₅=20Ω，R₂= R₄= R₆=180Ω，电压U_S1=U_S2=U_S3=110V，当开关S断开和闭合时，分别求电路中各支路电流。

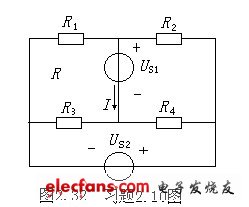
2．10在图2．３2所示电路中，已知电阻R₁=4Ω，R₂=8Ω，R₃=6Ω，R₄=12Ω，电压U_S1=1.2V，U_S2=3V，用叠加定理求电流I。

2．11在图2．３3所示电路中，已知电阻R₁=R₃=1Ω，R₂=2Ω，R₄=R₅=3Ω，电压U_S4=3V，I_S1=9A，用叠加定理求电压U₅。

2.12在图2．３4所示电路中，已知电阻R₁=40Ω，R₂=36Ω，R₃=R₄=60Ω，电压U_S1=100V，U_S2=90V，用叠加定理求电流I₂。

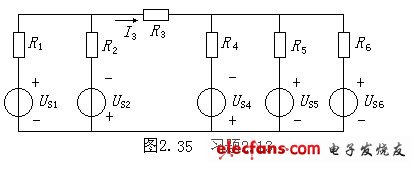
2．13在图2．35所示电路中，已知电阻R₁=3kΩ，R₂=6kΩ，R₃=1kΩ，R₄=R₆=2kΩ，R₅=1kΩ，电压U_S1=15V，U_S2=12V，U_S4=8V，U_S5=7V，U_S6=11V，试用戴维宁定律求电流I₃。

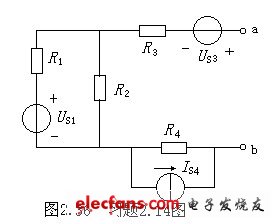
2．14在图2．36所示电路中，已知电阻R₁= R₂=2Ω，R₃=50Ω，R₄=5Ω，电压U_S1=6V，U_S3=10V，I_S4=1A，求戴维宁等效电路。

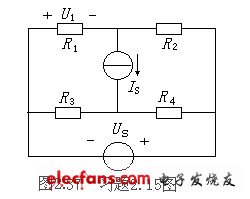
2．15在图2．37所示电路中，已知电阻R₁=3Ω，R₂=6Ω，R₃=1Ω，R₄=2Ω，电压U_S=3V，I_S=3A，试用戴维宁定律求电压U₁。

2．16在图2．38所示电路中，已知电阻R₁= R₂=4Ω，R₃=6Ω，电压U_S1=10V，U_S2=20V，求诺顿等效电路。

2．17在图2．39所示电路中，已知电阻R₁=R₆=4Ω，R₂=R₇=2Ω，R₃=5Ω，R₄=9Ω，R₅=8Ω，电压U_S1=40V，U_S2=20V，U_S7=10V，试用诺顿定律求电流I₄。

2．18在图2．４0所示电路中，已知电阻R₁=R₂=R₅=R₆=6Ω，R₃= R₄=3Ω，电压U_S=24V，I_S=1A，试用诺顿定律求电压U。